Question

Cho tam giác ABC cân tại A. Có AH là đường cao

a) Cm tam giác AHB= tam giác AHC

b) H là trung điểm của BC

c) AH là phân giác của tam giác ABC

Answer 1

`@` `\text {Ans}`

`\downarrow`

`a,`

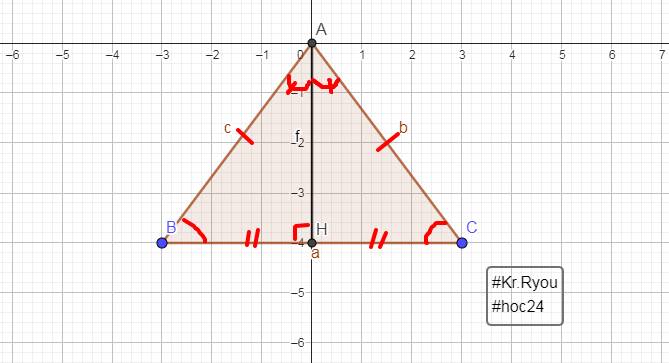
Vì `\Delta ABC` cân tại A

`-> \text {AB = AC,}` $\widehat {B} = \widehat {C}$

Vì `\text {AH}` là đường cao

`-> \text {AH} \bot \text {BC}`

`->` $\widehat {AHB} = \widehat {AHC} = 90^0$

Xét `2 \Delta` vuông `AHB` và `AHC`:

`\text {AB = AC}`

$\widehat {B} = \widehat {C}$

`=> \Delta AHB = \Delta AHC (ch-gn)`

`b,`

Vì `\Delta AHB = \Delta AHC (a)`

`-> \text {HB = HC (2 cạnh tương ứng)}`

`-> \text {H là trung điểm của BC}` 

Hoặc bạn có thể dùng cách này (nếu đã học về tính chất của `\Delta` cân đối với các đường trong `\Delta`)

Vì `\Delta ABC` cân tại A.

Mà `\text {AH}` là đường cao

`@` Theo tính chất của `\Delta` cân với các đường trong `\Delta`

`-> \text {AH cũng là đường trung tuyến}`

`-> \text {H là trung điểm của BC}`

`c,`

Vì `\Delta AHB = \Delta AHC (a)`

`->` $\widehat {BAH} = \widehat {CAH} (\text {2 góc tương ứng})$

`-> \text {AH là tia phân giác của} \Delta ABC`

Hoặc bạn có thể dùng cách này (nếu đã học về tính chất của `\Delta` cân đối với các đường trong `\Delta`)

Vì `\Delta ABC` cân tại A.

Mà `\text {AH}` là đường cao

`@` Theo tính chất của `\Delta` cân với các đường trong `\Delta`

`-> \text {AH cũng là đường phân giác}`

Answer 2

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có

AB=AC

AH chung

=>ΔAHB=ΔAHC

b: ΔAHB=ΔAHC

=>HB=HC

=>H là trung điểm của BC

c: ΔABC cân tại A

mà AH là trung tuyến

nên AH là phân giác