Chứng minh Ax// By
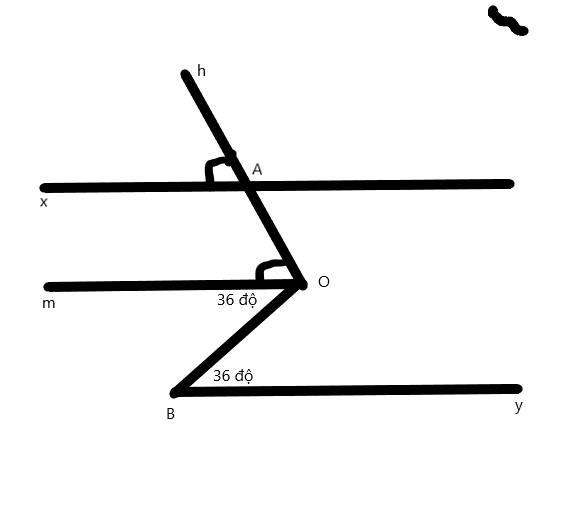 a) chứng minh Ax//Om
a) chứng minh Ax//Om
b) chứng minh Ax//By
a: góc hAx=góc mOA
mà hai góc này đồng vị
nên Ax//Om
b: góc mOA=góc yBO
mà hai góc này so le trong
nên Om//By
mà Ax//Om
nên Ax//By
a) Ta có:
\(\widehat{xAh}=\widehat{mOA}\) (gt) nên hai góc này là hai góc đồng vị
⇒ Ax//Om
b) Ta có:
\(\widehat{OBy}=\widehat{mOB}=36^o\) nên hai góc này là hai góc so le trong
⇒ By//Om
Mà: Ax//Om (cmt)
⇒ Ax//By
Ta có :
góc `hAx` = góc `AOM`
Mà 2 góc này ở vị trí đồng vị
`=>` góc `hAx = góc AOM`
`=> Ax//Om`
`b)`
ta có : `góc mOB = góc OBy`
Mà 2 góc này ở vị trí sole trong
`=> Om // By`
lại có `Ax//OM`
`Om//By => Ax//By`
mn giúp mik câu toán này với
mik cảm ơn nhiều
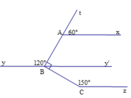
Bài 5: Cho bài toán như hình vẽ
a/ Chứng minh: Ax//By
b/ Chứng minh: By//Cz
c/ Chứng minh: Ax//By//Cz
Giải:
Ta có.....
a) ta có: \(\widehat{BAx}+\widehat{ABy}=60^o+120^o=180^o\)
Mà 2 góc này là 2 góc trong cùng phía ⇒Ax//By
b) ta có: \(\widehat{CBy}+\widehat{BCz}=140^o+40^o=180^o\)
Mà 2 góc này là 2 góc trong cùng phía ⇒By//Cz
c) Ax//By, By//Cz⇒Ax//Cz
a)Vì A trong cùng phía vói B1 -->Ax//By(B1 là góc B bằng 120o )
b)Vì B2 so le trong với Cz--->B2//Cz(B2 là góc B bằng 140o )
c)Ax//By,By//Cz
---->Ax//Cz
-->Ax//By//Cz.
Cho đường tròn (O) đường kính AB, vẽ tiếp tuyến Ax và By (Ax, By cùng nằm trên nửa mặt phẳng bờ AB). M ϵ Ax; Từ M vẽ tiếp tuyến MQ (Q là tiếp điểm), MQ cắt By tại E.
a) Chứng minh: AM + BE = ME
b) Chứng minh: OM ┸ OE
c) Chứng minh: AM.BE = OB
a: Xét (O) có
MA là tiếp tuyến có A là tiếp điểm
MQ là tiếp tuyến có Q là tiếp điểm
Do đó: MA=MQ
Xét (O) có
EQ là tiếp tuyến có Q là tiếp điểm
EB là tiếp tuyến có B là tiếp điểm
Do đó: EQ=EB
Ta có: QM+QE=EM
hay EM=AM+BE
Cho hình vẽ, chứng minh: Ax song song By ( Ax//By )
Lời giải:
Ta thấy:
$\widehat{yBA}+\widehat{BAx}=124^0+56^0=180^0$. Mà 2 góc này ở vị trí trong cùng phía nên $By\parallel Ax$ (đpcm)
\(Chứng minh Ax//By//Ct\)
Cho hình vẽ bên. Chứng minh:
a) Ax // By
b) By // Cz

a) Ta có tAx ^ + xAB ^ = 180 ∘ (hai góc kề bù) mà tAx ^ = 60 ∘
⇒ xAB ^ = 180 ∘ − 60 ∘ = 120 ∘
Mặt khác ABy ^ = 120 ∘
⇒ xAB ^ = ABy ^ mà hai góc này ở vị trí so le trong
⇒ Ax // By
b)
Kẻ tia By' là tia đối của tia By
Ta có: ABy ^ + ABy' ^ = 180 ∘ (hai góc kề bù) mà ABy ^ = 120 ∘
⇒ ABy' ^ = 180 ∘ − 120 ∘ = 60 ∘
Mặt khác ABC ^ = 90 ∘ hay ABy' ^ + y'BC ^ = 90 ∘
⇒ y'BC ^ = 90 ∘ − 60 ∘ = 30 ∘
Ta có y'BC ^ + CBy ^ = 180 ∘ (hai góc kề bù)
⇒ CBy ^ = 180 ∘ − 30 ∘ = 150 ∘
Ta lại có BCz ^ = 150 ∘
⇒ BCz ^ = CBy ^ mà hai góc này ở vị trí so le trong
⇒ By // Cz
chứng minh bất đẳng thức bunhiacopxki nếu (a^2+b^2)(x^2+y^2)=(ax+by)^2 thì ax=by
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
CHO TAM GIÁC ABC. TRONG NỬA MẶT PHẲNG BỜ AB CHỨA C, KẺ CÁC TIA AX VÀ BY SAO CHO C NẰM GIỮA HAI ĐƯỜNG THẲNG AX VÀ BY. CHỨNG MINH RẰNGA. NẾU AX // BY THÌ ACB = XAC + CBY.B. NẾU ACB = XAC + CBY THÌ AX // BY
Trong hình vẽ bên, cho ABC ̂ = 800, By là tia phân giác của ABC ̂.
Chứng minh rằng:
a) Ax ⫽ By theo hai cách b) Ax ⫽ Cz
chứng minh rằng : Ax // By
Ax//By khi mà nó // với nhau
???? tự nhiên chứng minh ax //by