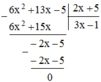x3+6x2-13x-42

Những câu hỏi liên quan
Trong các khai triển dưới đây, khai triển nào là đúng?
A. (x-2)3 = x3 - 6x2 +12x-8
B. (x-2)3 = x3 - 2x2 + 4x -8
C. (x-2)3 = 3x3 - 6x2 + 12x -24
D. (x-2)3 = x3 - 6x2 + 12x + 8
A. (x-2)3 = x3 - 6x2 +12x - 8 (hằng đẳng thức)
Đúng 0
Bình luận (0)
Làm tính chia: 6 x 2 + 13 x - 5 : 2 x + 5
Phân tích đa thức thành nhân tử : 6x2 – 13x + 6
\(6x^2-13x+6\)
\(=6x^2-9x-4x+6\)
\(=\left(2x-3\right)\left(3x-2\right)\)
Đúng 0
Bình luận (0)
Giải các phương trình sau:
13
x
-
3
2
x
+
7
+
1
2
x
+
7
6
x
2
-
9
Đọc tiếp
Giải các phương trình sau: 13 x - 3 2 x + 7 + 1 2 x + 7 = 6 x 2 - 9
13 x - 3 2 x + 7 + 1 2 x + 7 = 6 x 2 - 9 Đ K X Đ : x ≠ ± 3 v à x ≠ - 7 2 ⇔ 13 x + 3 x 2 - 9 2 x + 7 + x 2 - 9 2 x + 7 x 2 - 9 = 6 2 x + 7 x 2 - 9 2 x + 7
⇔ 13(x + 3) + x 2 – 9 = 6(2x + 7)
⇔ 13x + 39 + x 2 – 9 = 12x + 42
⇔ x 2 + x – 12 = 0
⇔ x 2 – 3x + 4x – 12 = 0
⇔ x(x – 3) + 4(x – 3) = 0
⇔ (x + 4)(x – 3) = 0
⇔ x + 4 = 0 hoặc x – 3 = 0
x + 4 = 0 ⇔ x = -4 (thỏa mãn)
x – 3 = 0 ⇔ x = 3 (loại)
Vậy phương trình có nghiệm x = -4.
Đúng 0
Bình luận (0)
tìm x biết
d) 6x2 + 13x + 3 = 0
Δ=13^2-4*6*3
=169-72=97>0
=>Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x=\dfrac{-13-\sqrt{47}}{12}\\x=\dfrac{-13+\sqrt{47}}{12}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Viết các biểu thức sau dưới dạng lập phương của tổng (hiệu).a) x3-6x2+12x-8 b) 8-12x+6x2-x3 c)x3+x2+dfrac{1}{3}x+dfrac{1}{27} d) dfrac{x^3}{8}+dfrac{3}{4}x2y+dfrac{3}{2}xy2+y3 e) (x-1)3-15.(x-1)2+75.(x-1)-125
Đọc tiếp
Viết các biểu thức sau dưới dạng lập phương của tổng (hiệu).
a) x3-6x2+12x-8 b) 8-12x+6x2-x3
c)x3+x2+\(\dfrac{1}{3}\)x+\(\dfrac{1}{27}\) d) \(\dfrac{x^3}{8}\)+\(\dfrac{3}{4}\)x2y+\(\dfrac{3}{2}\)xy2+y3 e) (x-1)3-15.(x-1)2+75.(x-1)-125
a)
=(x-2)3
b)\(\left(2-x\right)^3\)
c)\(\left(x+\dfrac{1}{3}\right)^3\)
d)\(\left(\dfrac{x}{2}+y\right)^3\)
e)
\(=\left(x-1\right)^2\left(x-1-15\right)+25\left[3\left(x-1\right)-5\right]\)
\(=\left(x-1\right)^2\left(x-16\right)+25\left(3x-3-5\right)\)
\(=\left(x-1\right)^2\left(x-16\right)+25\left(3x-8\right)\)
Đúng 1
Bình luận (0)
Cho đồ thị hàm số
y
x
3
-
6
x
2
+
9
x
-
2
như hình vẽKhi đó phương trình
|
x
3
-
6
x
2
+
9
x
-
2
|
m
(m là tham số ) có 6 nghiệm phân biệt k...
Đọc tiếp
Cho đồ thị hàm số y = x 3 - 6 x 2 + 9 x - 2 như hình vẽ
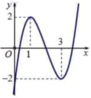
Khi đó phương trình | x 3 - 6 x 2 + 9 x - 2 | = m (m là tham số ) có 6 nghiệm phân biệt khi và chỉ khi
A. -2≤m≤2
B. 0<m<2
C. 0≤m≤2
D. -2<m<2
Chọn B
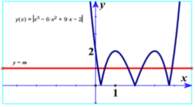
+ Đồ thị hàm số y = | x 3 - 6 x 2 + 9 x - 2 | có được bằng cách biến đổi đồ thị (C) hàm số y = x 3 - 6 x 2 + 9 x - 2
Giữ nguyên phần đồ thị (C) nằm trên trục hoành.
Lấy đồi xứng phần đồ thị của (C) phần dưới trục hoành qua trục hoành.
Xóa phần đồ thị còn lại (C) phía dưới trục hoành.
+ Số nghiệm của phương trình | x 3 - 6 x 2 + 9 x - 2 | = m là số giao điểm của đồ thị hàm số
y = | x 3 - 6 x 2 + 9 x - 2 | và đồ thị hàm số y=m. Để phương trình có 6 nghiệm phân biệt thì điều kiện cần và đủ là 0<m<2.
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử:
a) 3x2 - 6xy.
b) x3 - 6x2 + 9x.
c) x2 - 2xy - 3y + 6y.
d) 6x2 - 19x + 15.
a) \(3x^2-6xy=3x\left(x-2y\right)\)
b) \(x^3-6x^2+9x=x\left(x^2-6x+9\right)=x\left(x-3\right)^2\)
c) \(=x\left(x-2y\right)-3\left(x-2y\right)=\left(x-2y\right)\left(x-3\right)\)
d) \(=2x\left(3x-5\right)-3\left(3x-5\right)=\left(3x-5\right)\left(2x-3\right)\)
Đúng 0
Bình luận (0)
\(a,=3x\left(x-2y\right)\\ b,=x\left(x-3\right)^2\\ c,Sửa:x^2-2xy-3x+6y=x\left(x-2y\right)-3\left(x-2y\right)=\left(x-2y\right)\left(x-3\right)\\ d,=\left(3x-5\right)\left(2x-3\right)\)
Đúng 1
Bình luận (0)
a, `3x^2-6xy=3x(x-2y)`
b, `x^3-6x^2+9x=x(x^2-6x+9)=x(x-3)^2`
c, `x^2-2xy-3y+6y=x^2-2xy+3y`
d, `6x^2-19x+15=6x^2-9x-10x+15=3x(2x-3)-5(2x-3)=(3x-5)(2x-3)`
Đúng 0
Bình luận (0)
x3-6x2+5x=0
\(x^3-6x^2+5x=0\Leftrightarrow x\left(x^2-6x+5\right)=0\)
\(\Leftrightarrow x\left(x^2-x-5x+5\right)=0\)
\(\Leftrightarrow x\left[x\left(x-1\right)-5\left(x-1\right)\right]=0\Leftrightarrow x\left(x-1\right)\left(x-5\right)=0\Leftrightarrow x=0;x=1;x=5\)
Đúng 1
Bình luận (0)
\(x^3-6x^2+5x=0\)
\(\Leftrightarrow x.\left(x^2-6x+5\right)=0\)
\(\Leftrightarrow x.\left(x^2-x-5x+5\right)=0\)
\(\Leftrightarrow x.\left[\left(x^2-x\right)-\left(5x-5\right)\right]=0\)
\(\Leftrightarrow x.\left[x\left(x-1\right)-5\left(x-1\right)\right]=0\)
\(\Leftrightarrow x\left(x-1\right)\left(x-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-1=0\\x-5=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=5\end{matrix}\right.\)
Vậy \(x\in\left\{0;1;5\right\}\)
Đúng 0
Bình luận (0)
Cho hàm số
y
-
x
3
+
6
x
2
-
9
x
+
4
là bảng biến thiên như hình bên dướiCác giá trị của tham số m sao cho phương trình
-
x
3
+
6
x
2
-
9
x
-
m
0
có ba nghiệm phân biệt là A. -3 m 1 B. 0 m 4 C. -4 m 0 D. 1 m...
Đọc tiếp
Cho hàm số y = - x 3 + 6 x 2 - 9 x + 4 là bảng biến thiên như hình bên dưới
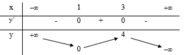
Các giá trị của tham số m sao cho phương trình - x 3 + 6 x 2 - 9 x - m = 0 có ba nghiệm phân biệt là
A. -3 < m < 1
B. 0 < m < 4
C. -4 < m < 0
D. 1 < m < 3