\(\dfrac{QH}{HR}=\dfrac{1}{2}\Rightarrow HR=2QH\)

Xét tam giác PQR vuông tại P có PH là đường cao ta có:

\(PH^2=HR\cdot QH\)

\(\Rightarrow4^2=2QH\cdot QH\)

\(\Rightarrow16=2QH^2\)

\(\Rightarrow QH^2=8\)

\(\Rightarrow QH=2\sqrt{2}\left(cm\right)\)

\(\Rightarrow HR=2\cdot2\sqrt{2}=4\sqrt{2}\left(cm\right)\)

\(\Rightarrow QR=4\sqrt{2}+2\sqrt{2}=6\sqrt{2}\left(cm\right)\)

Câu 1: C

Câu 2: A

Câu 3: D

Ta có: \(\dfrac{BH}{HC}=\dfrac{1}{2}\)

nên HC=2HB

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền AB, ta được:

\(AH^2=HB\cdot HC\)

\(\Leftrightarrow HB\cdot2HB=4^2=16\)

\(\Leftrightarrow HB^2=8\)

hay \(HB=2\sqrt{2}\left(cm\right)\)

\(\Leftrightarrow HC=2\cdot HB=2\cdot2\sqrt{2}=4\sqrt{2}\left(cm\right)\)

\(\Leftrightarrow HB+HC=2\sqrt{2}+4\sqrt{2}\)

hay \(BC=6\sqrt{2}\left(cm\right)\)

Có:

\(\dfrac{AB}{AC}=\dfrac{4}{3}=\dfrac{4k}{3k}\) (k là số bất kì)

\(\Rightarrow AB=4k,AC=3k\)

Áp dụng đl pytago vào tam giác ABC được:

\(BC^2=AB^2+AC^2=\left(4k\right)^2+\left(3k\right)^2=16k^2+9k^2=25k^2=\left(5k\right)^2\\ \Rightarrow BC=5k\left(cm\right)\)

Theo hệ thức lượng, có:

\(AH.BC=AB.AC\\ \Leftrightarrow3,6.5k=4k.3k\\ \Leftrightarrow18=12k\\ \Rightarrow k=\dfrac{18}{12}=\dfrac{3}{2}\)

\(\Rightarrow\left\{{}\begin{matrix}AB=4k=4.\dfrac{3}{2}=6\left(cm\right)\\AC=3k=3.\dfrac{3}{2}=\dfrac{9}{2}=4,5\left(cm\right)\\BC=5k=5.\dfrac{3}{2}=\dfrac{15}{2}=7,5\left(cm\right)\end{matrix}\right.\)

\(\Rightarrow P_{ABC}=AB+AC+BC=6+4,5+7,5=18\left(cm\right)\)

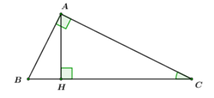
Áp dụng định lý Pytago trong ∆ ABC vuông tại A ta có:

Áp dụng hệ thức lượng trong  ∆ ABC vuông tại A có đường cao AH ta có:

Đáp án cần chọn là: B

1: Xét ΔABC vuông tại A có 

\(BC^2=AB^2+AC^2\)

hay BC=5(cm)

Xét ΔABC vuông tại A có AH là đường cao

nên \(AH\cdot BC=AB\cdot AC\)

hay AH=2,4(cm)

xem lại đề bạn ơi phân giác BD hay AD?

Bài này tính toán được bình thường dù phân giác AD

Nhưng kết quả vô cùng xấu, bạn kiểm tra lại số liệu

(Hệ thức lượng \(AB^2=BH.BC\) tính được \(BC=\dfrac{80}{9}\), sau đó Pitago tính AC thì nhận được 1 kết quả vô cùng xấu, dẫn tới việc sử dụng định lý phân giác \(\dfrac{BD}{AB}=\dfrac{DC}{AC}\) để tính toán BD, DC sẽ cho 1 kết quả xấu còn kinh khủng hơn)

Áp dụng định lý Pitago:

\(AB=\sqrt{AH^2+BH^2}=\sqrt{41}\)

Áp dụng hệ thức lượng:

\(AB^2=BH.BC\Rightarrow BC=\dfrac{AB^2}{BH}=\dfrac{41}{4}\)

Áp dụng Pitago:

\(AC=\sqrt{BC^2-AB^2}=\dfrac{5\sqrt{41}}{4}\)

Chu vi: \(AB+AC+BC=\dfrac{41+9\sqrt{41}}{4}\left(cm\right)\)