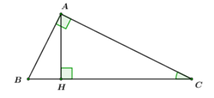
Áp dụng định lý Pytago trong ∆ ABC vuông tại A ta có:
![]()
Áp dụng hệ thức lượng trong ∆ ABC vuông tại A có đường cao AH ta có:
![]()
![]()
Đáp án cần chọn là: B

Áp dụng định lý Pytago trong ∆ ABC vuông tại A ta có:
![]()
Áp dụng hệ thức lượng trong ∆ ABC vuông tại A có đường cao AH ta có:
![]()
![]()
Đáp án cần chọn là: B
1. Cho tam giác ABC vuông tại A, đường cao AH, biết AB=4cm,AC=9cm. Tính sin B, sin C
2.Cho tam giác ABC vuông tại A, Cos B= an pha, Cos = 4/5. Tính sin, tan,cos
3. Cho tam giác ABC vuông tại A, đường cao AH, biết AB=6cm, BC= 10cm
a. Tính AC,AH. Tỉ số đồng giác góc B,C
b. Gọi E,F lần lượt là hình chiếu H lên AB,AC. CM :AE.AD=AF.AC
c. Tính S tứ giác AEHF
Cho tam giác ABC vuông ở A, đường cao AH, AB = 3cm, AC = 4 cm
a, Tính độ dài các đoạn thẳng BC và AH
b, Tính số đo B ^ ; C ^
c, Đường phân giác trong
C
^
cắt cạnh BC tại E. Tính độ dài các đoạn thẳng BE, CE và AE
Cho tam giác ABC vuông tại A đường cao AH có AB=\(\frac{1}{3}\)AC
a Tính góc B và C
b Tính tỉ số \(\frac{BH}{CH}\)
c Tính S tam giác ABH biết S tam giác ABC=15 cm2
Cho tam giác ABC vuồn tại A và đường cao AH biết AB=15 cm, BC=25cm.
a) Tính AH, BH
b) Từ B vẽ ddouot vuông góc BC cắt AC tại D. Vẽ tia ohaan giác góc C cắt AB, DB lần lượt tại M, N. CM: CN.CD= CM.CB
c) Gọi O là giao điểm của CD và AH. CM: Tam giác OAN cân
Tam giác ABC cân tại A, đường cao AH. Đường thẳng vuông góc với AC tại C cắt AH tại O. Tia Ax nằm trong góc BAC cắt đường tròn tâm O bán kính OC tại M và N (AM < AN). Gọi K là chân đường vuông góc của O lên Ax.
a) Chứng minh rằng các điểm A, B, C, O, H thuộc một đường tròn
b) Biết AH = 24 cm và OH = 6 cm. tính chu vi tam giác ABC
c) Tia AH cắt đường tròn (O; OC) tại E và F (AE < AF). Chứng minh rằng AE.FH = AF.EH
d) Gọi G là trọng tâm tam giác CMN. Khi Ax di động trong góc BAC thì G chạy trên đường nào?
Cho tam giác ABC vuông tại A có đường cao AH và AB = 3 cm, AC = 4cm .Tính
a) BC ?
b) AH =?
c) góc C =?
Bài 1: Cho tam giác ABC nhọn (AB<AC) nội tiếp (O). Gọi AD,BE,CF là 3 đường cao cắt nhau tại H.
a) Cm: B,C,E,F cùng thuộc 1 đường tròn. Xác định tâm M của đường tròn này
b) Gọi AK là đường kính của (O). Cm: BHCK là hình bình hành
c) Gọi I là trung điểm AH. Cm: IE là tiếp tuyến của (M)
d) Cho AH=5cm, DB=4cm, DC=6cm. Tính diện tích tam giác ABC
Bài 2: Cho tam giác ABC nhọn có góc BAC=45 độ. Các đường cao BE,CF cắt nhau tại H. Gọi O là trung điểm BC
a) Cm: tam giác AEF đồng dạng tam giác ABC và EF = AH/ (căn 2)
b) Cm: tam giác OEF vuông cân và diện tích tam giác AEF= diện tích tứ giác BCEF
c) Cm: trong các tam giác vuông có chiều cao ứng với cạnh huyền không đổi, tam giác vuông cân có chu vi nhỏ nhất
Bài 3: Cho (O;R) và (O' ; R') cắt nhau tại A và (R>R'). Tiếp tuyến chung EF của (O) và (O') cắt tia đối của tia AB tại C (E thuộc (O), F thuộc (O')). Gọi (I) và (J) lần lượt là tâm của 2 đường tròn ngoại tiếp tam giác OEC và tam giác O'FC
a) Cm: (I) cắt (J)
b) Gọi D là giao điểm cùa (I) và (J) (D # C). Cm: A,B,D thẳng hàng
c) Gọi M là điểm đối xứng của E qua OC, N là điểm đối xứng của F qua O'C. Cm" E,F,M,N cùng thuộc 1 đường tròn, xác định tâm đường tròn này
Bài 4: Cho tam giác ABC, vẽ (I;r) tiếp xúc AB,BC,CA lần lượt tại M,N,S.
a) Cm: AB+AC-BC=2M
b) Cho AB=7cm, BC=6cm, AC=4cm. Tính MA,NB,SC
c) Giả sử tam giác ABC vuông tại A, R và r là bán kính của đường tròn ngoại tiếp và nội tiếp của tam giác
Cm: AB+AC=2(R+r)
Các bạn không cần làm hết đâu ạ, câu nào các bạn biết thì các bạn làm dùm mình rồi gửi câu trả lời cho mình nha. Mình cần gấp lắm ạ!!!! Mong các bạn giúp mình
Câu 1 : Cho Tam Giác ABC ( A = 90 độ ) biết AB = 3 Cm , C = 30 độ . Tính AC , BC
Câu 2 : Cho Tam Giác ABC Vuông Tại A , Đường Cao AH . Biết HB = 9 Cm , HC=16Cm
a , Tính AB , Ac , Ah
b, Gọi D Và E Lần Lượt Là Hình Chiếu Vuông Góc Của H Trên AB Và AC . Tứ Giác ADHE Là Hình Gì ? Chứng Minh
c , Tính Chu Vi Và Diện Tích Của Tứ Giác Đó
Câu 3 : Cho Tam Giác ABC Vuông Tại A , Đường Cao AH , Biết BH = a , CH = b
Chứng Minh : Căn Bậc Hai Của ab bé hơn hoặc bằng a+b/2
Cho tam giác ABC vuông tại A có AB = 3 cm, BC = 6 cm.
a) Tính độ dài cạnh AC, số đo góc B và góc C
b) Vẽ (O) ngoại tiếp tam giác ABC. Đường cao AH của tam giác ABC cắt (O) tại D. Chứng minh BC là đường trung trực của AD
c) Tiếp tuyến tại D của (O) cắt BC tại E. Chứng minh EA là tiếp tuyến của (O)
d) Chứng minh EA^2 = EB.EC
Cho tam giác ABC vuông tại A nội tiếp đường tròn (O) . Kẻ đường cao AH , đường tròn (I) đường kính AH cắt AB , AC và đường tròn (O) lần lượt ở D, E , S . Á cắt đường thẳng BC tại S
cm ) tứ giác ADHE là hình chữ nhật
b) BDEC nội tiếp
c) OA vuông góc với DE và 3 điểm S, D , E thẳng hàng