Đk: \(x\ge1\)

\(\Leftrightarrow4\left(2\sqrt{x-1}-1\right)+\left(4x-5\right)\left(x+2\right)=0\)

\(\Leftrightarrow\dfrac{4\left(4x-5\right)}{2\sqrt{x-1}+1}+\left(4x-5\right)\left(x+2\right)=0\)

\(\Leftrightarrow\left(4x-5\right)\left(\dfrac{4}{2\sqrt{x-1}+1}+x+2\right)=0\)

\(\Leftrightarrow x=\dfrac{5}{4}\)(Dễ thấy ngoặc to lớn hơn 0 với \(x\ge1\))

Muốn giải mấy bài kiểu này thì mình hay đoán nghiệm trước

Việc đoán nghiệm thì có thể dùng kinh nghiệm hoặc bấm máy tính

Ở đây mình đoán được nghiệm là x=5/4 nên ta sẽ cố gắng tạo ra nhân tử dạng

4x-5 hoặc x-(5/4) ở đầy mình chọn nhân tử 4x-5

Trong những phương trình chứa căn thức thì để tạo nhân tử thì cách thường dùng nhất là phép liên hợp

Phép liên hợp là phép kiểu: \(\sqrt{a}-\sqrt{b}=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{a}+\sqrt{b}}=\dfrac{a-b}{\sqrt{a}+\sqrt{b}}\)

Ok, ta biến đổi pt lại để tạo nhân tử 4x-5:

\(\left(8\sqrt{x-1}-4\right)+\left(4x^2+3x-10\right)=0\) (ở đây ta thay x=5/4 vào 8căn(x-1) thì được 4 nên ta sẽ ghép với 4, còn phần còn lại của pt thì gộp lại chung)

\(\dfrac{4\left(2\sqrt{x-1}-1\right)\left(2\sqrt{x-1}+1\right)}{2\sqrt{x-1}+1}+\left(4x-5\right)\left(x+2\right)=0\)(sử dụng phép liên hợp)

\(\Leftrightarrow\dfrac{4\left(4x-5\right)}{2\sqrt{x-1}+1}+\left(4x-5\right)\left(x+2\right)=0\)

\(\Leftrightarrow\left(4x-5\right)\left(\dfrac{4}{2\sqrt{x-1}+1}+x+2\right)=0\)

Ở đây thì với đk x>=1 thì ngoặc to sẽ lớn hơn 0 nên kêt luận x=5/4

2:

a: =>2x^2-4x-2=x^2-x-2

=>x^2-3x=0

=>x=0(loại) hoặc x=3

b: =>(x+1)(x+4)<0

=>-4<x<-1

d: =>x^2-2x-7=-x^2+6x-4

=>2x^2-8x-3=0

=>\(x=\dfrac{4\pm\sqrt{22}}{2}\)

Mình khuyên bạn thế này : 

Bạn nên tách những câu hỏi ra 

Như vậy các bạn sẽ dễ giúp

Và cũng có nhiều bạn giúp hơn !

Bài 1.

a) ( x - 3 )( x + 7 ) = 0

<=> x - 3 = 0 hoặc x + 7 = 0

<=> x = 3 hoặc x = -7

Vậy S = { 3 ; -7 }

b) ( x - 2 )² + ( x - 2 )( x - 3 ) = 0

<=> ( x - 2 )( x - 2 + x - 3 ) = 0

<=> ( x - 2 )( 2x - 5 ) = 0

<=> x - 2 = 0 hoặc 2x - 5 = 0

<=> x = 2 hoặc x = 5/2

Vậy S = { 2 ; 5/2 }

c) x² - 5x + 6 = 0

<=> x² - 2x - 3x + 6 = 0

<=> x( x - 2 ) - 3( x - 2 ) = 0

<=> ( x - 2 )( x - 3 ) = 0

<=> x - 2 = 0 hoặc x - 3 = 0

<=> x = 2 hoặc x = 3

Bài 2.

a) \(\frac{x}{x+1}-1=\frac{3}{2}x\)

ĐKXĐ : x khác -1

<=> \(\frac{x}{x+1}-\frac{x+1}{x+1}=\frac{3}{2}x\)

<=> \(\frac{-1}{x+1}=\frac{3x}{2}\)

=> 3x( x + 1 ) = -2

<=> 3x² + 3x + 2 = 0

Vi 3x² + 3x + 2 = 3( x² + x + 1/4 ) + 5/4 = 3( x + 1/2 )² + 5/4 ≥ 5/4 > 0 ∀ x

=> phương trình vô nghiệm

b) \(\frac{4x}{x-2}-\frac{7}{x}=4\)

ĐKXĐ : x khác 0 ; x khác 2

<=> \(\frac{4x^2}{x\left(x-2\right)}-\frac{7x-14}{x\left(x-2\right)}=\frac{4x^2-8x}{x\left(x-2\right)}\)

=> 4x² - 7x + 14 = 4x² - 8x

<=> 4x² - 7x - 4x² + 8x = -14

<=> x = -14 ( tm )

Vậy phương trình có nghiệm x = -14

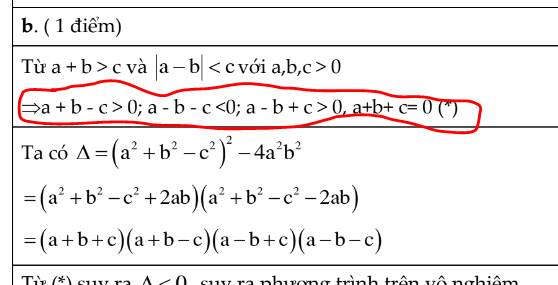
Lời giải:

Từ $a+b> c\Rightarrow a+b-c>0$ (cái này hiển nhiên) 

Từ $|a-b|< c\Leftrightarrow |a-b|^2< c^2$

$\Leftrightarrow (a-b)^2< c^2$

$\Leftrightarrow (a-b-c)(a-b+c)<0$

Với $c>0$ thì $a-b-c< a-b+c$ nên để tích âm thì $a-b-c<0< a-b+c$

Hay $a-b-c<0$ và $a-b+c>0$

\(a.-3x^2+15x=0\)

\(\Leftrightarrow3x\left(-x+5\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}3x=0\\-x+5=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=5\end{matrix}\right.\)

\(b.2x^2-32=0\)

\(\Leftrightarrow2x^2=32\)

\(\Leftrightarrow x^2=16\)

\(\Leftrightarrow\left|x\right|=4\)

\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-4\end{matrix}\right.\)

\(c.2x^2-5x+1=0\)

\(a=2;b=-5;c=1\)

\(\Delta=\left(-5\right)^2-4.2.1=17>0\)

Do \(\Delta>0\) nên phương trình có 2 nghiệm phân biệt:

\(x_1=\dfrac{5+\sqrt{17}}{4}\)

\(x_2=\dfrac{5-\sqrt{17}}{4}\)

\(a,-3x^2+15x=0\\ -3x\left(x-5\right)=0\\ \Rightarrow\left\{{}\begin{matrix}x=0\\x-5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\x=5\end{matrix}\right.\) 

\(b,\\ 2\left(x^2-16\right)=0\\ \Leftrightarrow x^2-16=0\\ \Leftrightarrow\left(x-4\right)\left(x+4\right)=0\\ \Rightarrow\left\{{}\begin{matrix}x=4\\x=-4\end{matrix}\right.\) 

\(c,\\ \Delta=5^2-4.2=17\\ \Rightarrow x_1,x_2=\dfrac{\Delta\pm b}{2ac}\\ =\dfrac{5\pm\sqrt{17}}{4}\)

a

\(\Leftrightarrow\left(\sqrt{x}-1\right)^2=0\\ \Leftrightarrow\sqrt{x}-1=0\\ \Leftrightarrow\sqrt{x}=1\\ \Leftrightarrow x=1^2=1\)

b

ĐK: \(x\ge0\)

\(\Leftrightarrow x+\sqrt{x}-3\sqrt{x}-3=0\\ \Leftrightarrow x+\sqrt{x}-\left(3\sqrt{x}+3\right)=0\\ \Leftrightarrow\sqrt{x}\left(\sqrt{x}+1\right)-3\left(\sqrt{x}+1\right)=0\\ \Leftrightarrow\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}+1=0\\\sqrt{x}-3=0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}=-1\left(loại\right)\\x=9\left(nhận\right)\end{matrix}\right.\)

a: =>(căn x-1)^2=0

=>căn x-1=0

=>x=1

b: =>(căn x-3)(căn x+1)=0

=>căn x-3=0

=>căn x=3

=>x=9

Lời giải:

a. ĐK: $x\geq 0$

$x-2\sqrt{x}+1=0$

$\Leftrightarrow (\sqrt{x}-1)^2=0$
$\Leftrightarrow \sqrt{x}-1=0$
$\Leftrightarrow \sqrt{x}=1$

$\Leftrightarrow x=1$ (tm) 

b. ĐK: $x\geq 0$

PT $\Leftrightarrow (x+\sqrt{x})-(3\sqrt{x}+3)=0$

$\Leftrightarrow \sqrt{x}(\sqrt{x}+1)-3(\sqrt{x}+1)=0$

$\Leftrightarrow (\sqrt{x}+1)(\sqrt{x}-3)=0$

Vì $\sqrt{x}+1\geq 1>0$ với mọi $x\geq 0$ nên $\sqrt{x}-3=0$

$\Leftrightarrow \sqrt{x}=3$

$\Leftrightarrow x=9$ (tm)

1/ \(sinx=-\frac{1}{2}=sin\left(-\frac{\pi}{6}\right)\)

\(\Rightarrow\left[{}\begin{matrix}x=-\frac{\pi}{6}+k2\pi\\x=\frac{7\pi}{6}+k2\pi\end{matrix}\right.\)

b/ \(cos=-\frac{\sqrt{2}}{2}=cos\left(\frac{3\pi}{4}\right)\)

\(\Rightarrow x=\pm\frac{3\pi}{4}+k2\pi\)

c/ \(tanx=\sqrt{3}=tan\left(\frac{\pi}{3}\right)\)

\(\Rightarrow x=\frac{\pi}{3}+k\pi\)

d/ \(cotx=0\Rightarrow x=\frac{\pi}{2}+k\pi\)

2/

a/ \(sin^2x+sinx-2=0\)

\(\Leftrightarrow\left(sinx-1\right)\left(sinx+2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sinx=1\\sinx=-2\left(vn\right)\end{matrix}\right.\) \(\Rightarrow x=\frac{\pi}{2}+k2\pi\)

b/ \(cot^2x-2cotx-3=0\)

\(\Leftrightarrow\left(cotx+1\right)\left(cotx-3\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}cotx=-1\\cotx=3\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=-\frac{\pi}{4}+k\pi\\x=arccot3+k\pi\end{matrix}\right.\)

3/ \(\Leftrightarrow1-cos2x+1-cos4x+1-cos6x=3\)

\(\Leftrightarrow cos2x+cos6x+cos4x=0\)

\(\Leftrightarrow2coss4x.cos2x+cos4x=0\)

\(\Leftrightarrow cos4x\left(2cos2x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}cos4x=0\\cos2x=-\frac{1}{2}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}4x=\frac{\pi}{2}+k\pi\\2x=\frac{2\pi}{3}+k2\pi\\2x=-\frac{2\pi}{3}+k2\pi\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{8}+\frac{k\pi}{4}\\x=\frac{\pi}{3}+k\pi\\x=-\frac{\pi}{3}+k\pi\end{matrix}\right.\)