CMR xy //x'y'
Cho hai đường thẳng xy và x'y' phân biệt. Hãy nêu cách nhận biết xem hai đường thẳng xy và x'y' song song hay cắt nhau bằng dụng cụ thước đo góc
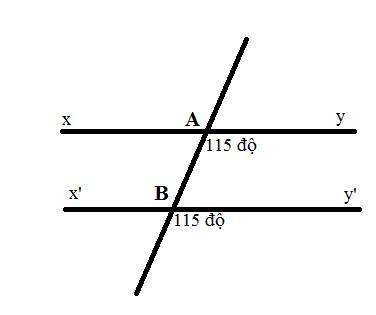
Chứng tỏ xy // x'y'
Vẽ lại hình:
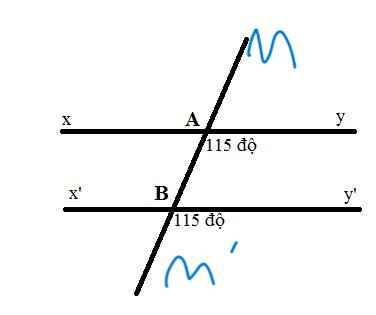
\(\widehat{x'BA}=\widehat{y'Bm'}\)(hai góc đối đỉnh)
=>\(\widehat{x'BA}=115^0\)
\(\widehat{x'BA}=\widehat{yAB}\)
mà hai góc này ở vị trí so le trong
nên xx'//yy'
Chứng tỏ xy // x'y'
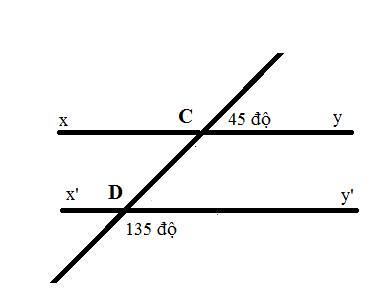
Vẽ lại hình:
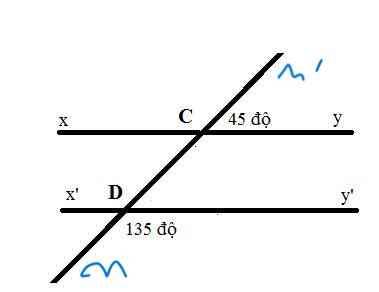
\(\widehat{y'DC}+\widehat{y'Dm}=180^0\)(hai góc kề bù)
=>\(\widehat{y'DC}=180^0-135^0=45^0\)
\(\widehat{y'DC}=\widehat{yCm'}\)=45 độ
mà hai góc này ở vị trí đồng vị
nên xy//x'y'
Chứng tỏ xy // x'y'
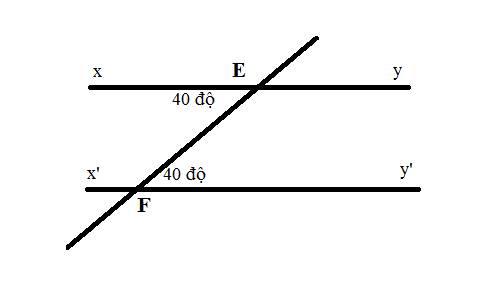
\(\widehat{xEF}=\widehat{y'FE}\)
mà hai góc này là hai góc ở vị trí so le trong
nên xy//x'y'
Có: \(\widehat{EFy'}=40^o;\widehat{xEF}=40^o\)
\(\Rightarrow \widehat{EFy'}=\widehat{xEF}\)
mà hai góc này đều nằm ở vị trí so le trong
nên \(xy//x'y'\)
Chứng tỏ xy // x'y'
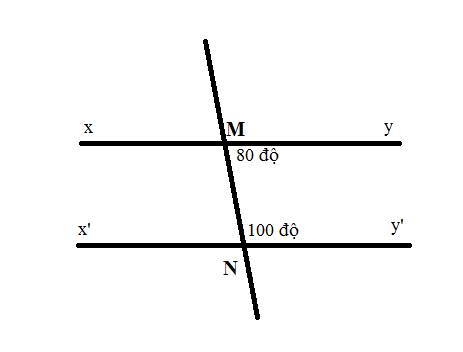
Ta có: \(\widehat{xMN}+\widehat{NMy}=180^o\)
\(\Rightarrow\widehat{xMN}=180^o-\widehat{NMy}\)
\(\Rightarrow\widehat{xMN}=180^o-80^o=100^o\)
Lại có: \(\widehat{MNy'}=100^o\)
\(\Rightarrow\widehat{xMN}=\widehat{MNy'}=100^o\)
Mà hai góc này ở vị trí so le trong
\(\Rightarrow xy//x'y'\)
Ta có: góc MNy' + MNx'=180 độ ( vì là 2 góc kề bù)
THay MNy' = 100 độ
Ta được MNx' = 180 độ - 100độ = 80 độ
Ta có góc yMN= MNx'( cùng =80 độ) mà yMN và MNx' ở vị trí so le trong của xy và x'y'
Nên xy// x'y'
2 cặp góc so le trong: x'NM = NMy, xMN = MNy'
4 cặp góc đồng vị: xMN = x'Nz, x'NM = xMz, yMN = y'Nz, y'NM = yMz
( z là đường thẳng cắt 2 đường thẳng )
LƯU Ý: 2 góc so le trong bằng nhau và 2 góc đồng vị bằng nhau
Cho đường thẳng xy // x'y', đường thẳng d cắt xy và x'y' lần lượt tại A và B. Kẻ tia phân giác AM của góc xAB, cắt x'y' tại M và tia phân giác BN của góc ABy' cắt xy tại N . Hãy chứng tỏ rằng :
a/ AM // BN
b/ góc AMB = góc ANB
Mọi người vẽ hình và giải giúp mình nhé, cảm ơn mọi người nhiều (mình đang cần gấp nhé)
CM: a) Do AM là tia p/giác của góc xAB nên :
\(\widehat{xAM}=\widehat{MAB}=\frac{\widehat{xAB}}{2}\)
Do BN là tia p/giác của góc ABy' nên :
\(\widehat{ABN}=\widehat{NBy'}=\frac{\widehat{ABy'}}{2}\)
Mà \(\widehat{xAB}=\widehat{ABy'}\) (so le trong vì xy // x'y')
=> \(\widehat{MAB}=\widehat{ABN}\)
mà 2 góc này ở vị trí so le trong
=> AM // BN (Đpcm)
b) Xét t/giác AMB và t/giác BNA
có : \(\widehat{MAB}=\widehat{ABN}\)(cmt)
AB : chung
\(\widehat{MBA}=\widehat{NAB}\) (so le trong vì xy // x'y')
=> t/giác AMB = t/giác BNA (g.c.g)
=> \(\widehat{AMB}=\widehat{ANB}\)(2 góc t/ứng)
Cho tam giác ABC đều. Qua B kẻ đường thẳng xy song song AC và hạ BM vuông góc với AC (M thuộc AC). Qua C kẻ đường thẳng x'y' song song AB và hạ CN vuông góc vói AB (N thuộc AB). Hai đường thẳng xy và x'y' cắt nhau tại P. Chứng minh:
a) Đường phân giác của góc A và hai đường BM, CN đồng quy;
b) Đường phân giác của góc A và hai đường thẳng xy và x'y' đồng quy.
Cho hai đường thẳng mn và xy vuông góc với nhau tại điểm M. vẽ đường thẳng x'y' vuông góc với đường thẳng mn tại điểm N(N khác m)
a) Chứng minh xy //x'y'
b) Trên các tia My,Ny' lần lượt lấy điểm C và D sao cho góc MCD=60 độ
Tính số đo góc NDC.
Cách làm:
B1: NHÌN KĨ VÀO SGK MỤC TỪ VUÔNG GÓC ĐẾN SONG SONG LÀ LÀM ĐƯỢC BÀI A
B2: LẬT LẠI MỤC TÍNH CHẤT HAI ĐƯƠNG THẲNG SONG SONG ĐỂ GIẢI BÀI B
ĐÃ XONG! THANKS
a) Ta có: \(xy\perp mn\) và \(x'y'\perp mn\)
\(\implies xy//x'y'\)
Vậy xy//x'y'(đpcm)
b) Ta có: \(xy//x'y'\) (câu a)
\(\implies \widehat{MCD}+\widehat{NDC}=180^0\) ( 2 góc trong cùng phía)
\(\implies 60^0+\widehat{NDC}=180^0\)
\(\implies \widehat{NDC}=180^0-60^0=120^0\)
Vậy góc NDC=120 độ.
_Học tốt_
Cho xy cắt x'y' tại O sao cho 2 góc xOx' bằng 3 góc x'Oy . Tính các góc tạo thành
Ta có: \(2.\widehat{xOx'}=3.\widehat{x'Oy}\)
\(\Rightarrow\frac{\widehat{xOx'}}{\widehat{x'Oy}}=\frac{3}{2}\)
\(\Rightarrow\widehat{xOx'}=180:\left(3+2\right).2=72^o\)
\(\Rightarrow\widehat{yOy'}=72^o\)( đối đỉnh với \(\widehat{xOx'}\))
\(\Rightarrow\widehat{x'Oy}=180:\left(3+2\right).3=108^o\)
\(\Rightarrow\widehat{xOy'}=108^o\)( đối đỉnh với \(\widehat{x'Oy}\))
P/s: Trình bày hơi xàm thông cảm :(
Cho hai đường thẳng xy và x'y' cắt nhau tại O. Bieetws xOx' - xOy' = 20 độ. Tính xOy', x'Oy, x'Oy'