Cho \(\overrightarrow{v}\)=(-2;3), đường thẳng d: 2x-3y+3=0, đường thẳng d1: 2x-3y-5=0. Tìm toạ độ của \(\overrightarrow{\text{w}}\) có giá vuông góc với đường thẳng d để d1 là ảnh của d qua phép tịnh tiến T\(\overrightarrow{\text{w}}\)

Những câu hỏi liên quan
cho overrightarrow{u} (3;-2),overrightarrow{v} (7;4) tính tọa độ của các vecto overrightarrow{u}+overrightarrow{v}, overrightarrow{u}-overrightarrow{v}, overrightarrow{8u},overrightarrow{3u}-overrightarrow{4v},-(overrightarrow{3u}-overrightarrow{4v})
Đọc tiếp
cho \(\overrightarrow{u}\) = (3;-2),\(\overrightarrow{v}\) = (7;4) tính tọa độ của các vecto \(\overrightarrow{u}\)+\(\overrightarrow{v}\), \(\overrightarrow{u}\)-\(\overrightarrow{v}\), \(\overrightarrow{8u}\),\(\overrightarrow{3u}\)-\(\overrightarrow{4v}\),-(\(\overrightarrow{3u}\)-\(\overrightarrow{4v}\))
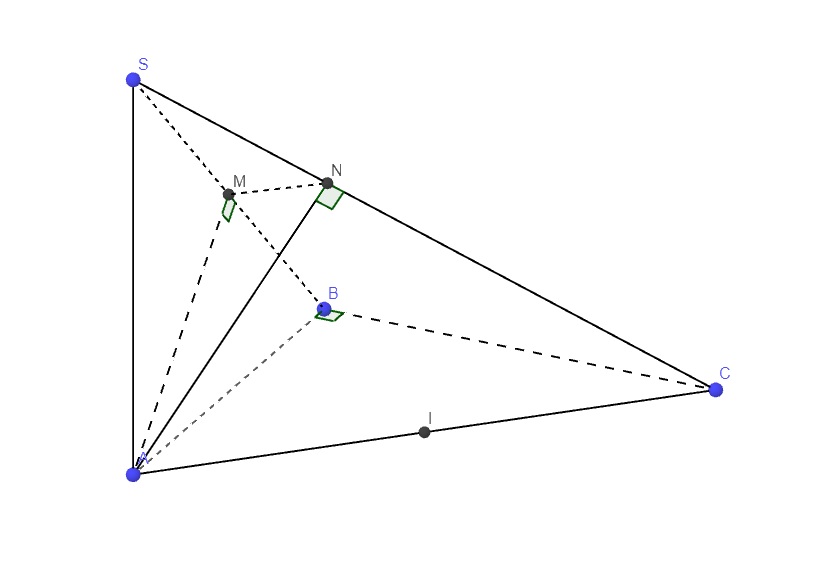
1/ Cho left|overrightarrow{u}right|sqrt{2} , left|overrightarrow{v}right|10 , overrightarrow{u}.overrightarrow{v}10. Tính số đó góc hợp giữa overrightarrow{u}vàoverrightarrow{v} . 2/ Cho hình chóp S.ABC, đáy là tâm giác vuông cân tại B, SA vuông góc với mặt đáy, AB SA aa. Tính góc 2mp ((SBC),(ABC))b. Gọi M,N lần lượt là hình chiếu của A lên SB, SC. Tam giác AMN là tam giác gì? tính góc giữa 2mp ((AMN),(ABC)), góc giữa (AC;(AMN)).c. Tính khoảng cách từ trung điểm I của đoạn thẳng AC đến mp (SBC...
Đọc tiếp
1/ Cho \(\left|\overrightarrow{u}\right|=\sqrt{2}\) , \(\left|\overrightarrow{v}\right|=10\) , \(\overrightarrow{u}.\overrightarrow{v}=10\). Tính số đó góc hợp giữa \(\overrightarrow{u}và\overrightarrow{v}\) .
2/ Cho hình chóp S.ABC, đáy là tâm giác vuông cân tại B, SA vuông góc với mặt đáy, AB = SA = a
a. Tính góc 2mp ((SBC),(ABC))
b. Gọi M,N lần lượt là hình chiếu của A lên SB, SC. Tam giác AMN là tam giác gì? tính góc giữa 2mp ((AMN),(ABC)), góc giữa (AC;(AMN)).
c. Tính khoảng cách từ trung điểm I của đoạn thẳng AC đến mp (SBC)
3/ Cho hình chóp S.ABCD, đáy là hình vuống tâm O, SA = SB = SC = SD = AB = 2a. M,N lần lượt là trung điểm SB, SD.
a. Tính số đo của góc giữa (MN;SC)
b. SA vuống góc với đường thẳng nào?
c. Tính a khoảng cách giữa d(AB;(SCD)).
CỨU MK VS, MAI MK KT 15' mà mk lại ko lm đc, ko bt lm lun, giúp mk vs, cảm ơn nhiều.
1.
\(cos\left(\widehat{\overrightarrow{u};\overrightarrow{v}}\right)=\dfrac{\overrightarrow{u}.\overrightarrow{v}}{\left|\overrightarrow{u}\right|.\left|\overrightarrow{v}\right|}=\dfrac{10}{10.\sqrt{2}}=\dfrac{1}{\sqrt{2}}\)
\(\Rightarrow\left(\widehat{\overrightarrow{u};\overrightarrow{v}}\right)=45^0\)
2.
a.
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\) (1)
Mà \(BC=\left(SBC\right)\cap\left(ABC\right)\Rightarrow\widehat{SBA}\) là góc giữa (SBC) và (ABC)
\(tan\widehat{SBA}=\dfrac{SA}{AB}=1\Rightarrow\widehat{SBA}=45^0\)
b.
Từ (1) \(\Rightarrow BC\perp AM\)
Mà \(AM\perp SB\left(gt\right)\) \(\Rightarrow AM\perp\left(SBC\right)\) (2)
\(\Rightarrow AM\perp MN\Rightarrow\Delta AMN\) vuông tại M
Từ (2) \(\Rightarrow AM\perp SC\), mà \(SC\perp AN\left(gt\right)\)
\(\Rightarrow SC\perp\left(AMN\right)\) (3)
Lại có \(SA\perp\left(ABC\right)\) theo giả thiết
\(\Rightarrow\) Góc giữa (AMN) và (ABC) bằng góc giữa SA và SC hay là góc \(\widehat{ASC}\)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(\Rightarrow tan\widehat{ASC}=\dfrac{AC}{SA}=\sqrt{2}\Rightarrow\widehat{ASC}\approx54^044'\)
Từ (3) \(\Rightarrow AN\) là hình chiếu vuông góc của AC lên (AMN)
\(\Rightarrow\widehat{CAN}\) là góc giữa AC và (AMN)
Mà \(\widehat{CAN}=\widehat{ASC}\) (cùng phụ \(\widehat{ACS}\)) \(\Rightarrow\widehat{CAN}=...\)
c.
\(\left\{{}\begin{matrix}IC=\dfrac{1}{2}AC\left(gt\right)\\AI\cap\left(SBC\right)=C\end{matrix}\right.\) \(\Rightarrow d\left(I;\left(SBC\right)\right)=\dfrac{1}{2}d\left(A;\left(SBC\right)\right)\)
Mà từ (2) ta có \(AM\perp\left(SBC\right)\Rightarrow AM=d\left(A;\left(SBC\right)\right)\)
\(SA=AB\left(gt\right)\Rightarrow\Delta SAB\) vuông cân tại A
\(\Rightarrow AM=\dfrac{1}{2}SB=\dfrac{a\sqrt{2}}{2}\Rightarrow d\left(I;\left(SBC\right)\right)=\dfrac{1}{2}AM=\dfrac{a\sqrt{2}}{4}\)
Đúng 1
Bình luận (0)
3.
a.
Do \(SA=SB=SC=SD\Rightarrow\) hình chiếu vuông góc của S lên (ABCD) trùng tâm O của hình vuông
Hay \(SO\perp\left(ABCD\right)\)
\(\Rightarrow SO\perp BD\)
Lại có \(AC\perp BD\) (hai đường chéo hình vuông)
\(\Rightarrow BD\perp\left(SAC\right)\Rightarrow BD\perp SC\)
Mà MN là đường trung bình tam giác SBD \(\Rightarrow MN||BD\)
\(\Rightarrow MN\perp SC\Rightarrow\left(\widehat{MN;SC}\right)=90^0\)
b.
\(AC=\sqrt{AB^2+BC^2}=2a\sqrt{2}\)
\(SA=SC=2a\Rightarrow SA^2+SC^2=8a^2=AC^2\)
\(\Rightarrow\Delta SAC\) vuông tại S (pitago đảo)
\(\Rightarrow SA\perp SC\)
c.
\(AB||CD\Rightarrow AB||\left(SCD\right)\Rightarrow d\left(AB;\left(SCD\right)\right)=d\left(A;\left(SCD\right)\right)\)
Lại có \(\left\{{}\begin{matrix}AC=2OC\\AO\cap\left(SCD\right)=C\end{matrix}\right.\) \(\Rightarrow d\left(A;\left(SCD\right)\right)=2d\left(O;\left(SCD\right)\right)\)
Từ O kẻ \(OE\perp CD\), từ \(O\) kẻ \(OF\perp SE\)
\(\Rightarrow OF\perp\left(SCD\right)\Rightarrow OF=d\left(O;\left(SCD\right)\right)\)
\(OE=\dfrac{1}{2}BC=a\) (đường trung bình)
\(\Delta SAC\) vuông tại S (theo cm câu b) \(\Rightarrow SO=\dfrac{1}{2}AC=a\sqrt{2}\) (trung tuyến ứng với cạnh huyền)
Hệ thức lượng:
\(OF=\dfrac{SO.OE}{\sqrt{SO^2+OE^2}}=\dfrac{a\sqrt{6}}{3}\)
\(\Rightarrow d\left(A;\left(SCD\right)\right)=2OF=\dfrac{2a\sqrt{6}}{3}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hai vecto \(\overrightarrow{u}\)=(2;a) và \(\overrightarrow{v}\)=(1;-1). Tính a để \(\overrightarrow{u}\).\(\overrightarrow{v}\)= 1
\(\overrightarrow{u}.\overrightarrow{v}=2.1+a.\left(-1\right)=2-a\)
\(\Rightarrow2-a=1\Rightarrow a=1\)
Đúng 0
Bình luận (0)
Cho tứ giác ABCD xác đinh I và số k sao cho véc tơ v đều bằng k.\(\overrightarrow{MI:}\overrightarrow{v}=\overrightarrow{MA}-\overrightarrow{MB}-2\overrightarrow{MC}\)
Trong mặt phẳng tọa độ Oxy, cho overrightarrow u (2; - 3),;overrightarrow v (4;1),;overrightarrow a (8; - 12)a) Hãy biểu thị mỗi vectơ overrightarrow u ,;overrightarrow v ,;overrightarrow a theo các vectơ overrightarrow i ,;overrightarrow j b) Tìm tọa độ của các vectơ overrightarrow u + ;overrightarrow v ,;4.;overrightarrow u c) Tìm mối liên hệ giữa hai vectơ overrightarrow u ,;overrightarrow a
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho \(\overrightarrow u = (2; - 3),\;\overrightarrow v = (4;1),\;\overrightarrow a = (8; - 12)\)
a) Hãy biểu thị mỗi vectơ \(\overrightarrow u ,\;\overrightarrow v ,\;\overrightarrow a \) theo các vectơ \(\overrightarrow i ,\;\overrightarrow j \)
b) Tìm tọa độ của các vectơ \(\overrightarrow u + \;\overrightarrow v ,\;4.\;\overrightarrow u \)
c) Tìm mối liên hệ giữa hai vectơ \(\overrightarrow u ,\;\overrightarrow a \)
a) Ta có: \(\overrightarrow u = (2; - 3)\)
\( \Rightarrow \overrightarrow u = 2.\;\overrightarrow i + \left( { - 3} \right).\;\overrightarrow j \)
Tương tự ta có: \(\overrightarrow v = (4;1),\;\overrightarrow a = (8; - 12)\)
\( \Rightarrow \overrightarrow v = 4.\;\overrightarrow i + 1.\;\overrightarrow j ;\;\;\overrightarrow a = 8.\;\overrightarrow i + \left( { - 12} \right).\;\overrightarrow j \)
b) Ta có: \(\left\{ \begin{array}{l}\overrightarrow u = 2.\;\overrightarrow i + \left( { - 3} \right).\;\overrightarrow j \\\overrightarrow v = 4.\;\overrightarrow i + 1.\;\overrightarrow j \end{array} \right.\)(theo câu a)
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}\overrightarrow u + \;\overrightarrow v = \left( {2.\;\overrightarrow i + \left( { - 3} \right).\;\overrightarrow j } \right) + \left( {4.\;\overrightarrow i + 1.\;\overrightarrow j } \right)\\4.\;\overrightarrow u = 4\left( {2.\;\overrightarrow i + \left( { - 3} \right).\;\overrightarrow j } \right)\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow u + \;\overrightarrow v = \left( {2.\;\overrightarrow i + 4.\;\overrightarrow i } \right) + \left( {\left( { - 3} \right).\;\overrightarrow j + 1.\;\overrightarrow j } \right)\\4.\;\overrightarrow u = 4.2.\;\overrightarrow i + 4.\left( { - 3} \right).\;\overrightarrow j \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow u + \;\overrightarrow v = 6.\;\overrightarrow i + \left( { - 2} \right).\;\overrightarrow j \\4.\;\overrightarrow u = 8.\;\overrightarrow i + \left( { - 12} \right).\;\overrightarrow j \end{array} \right.\end{array}\)
c) Vì \(\left\{ \begin{array}{l}4.\;\overrightarrow u = 8.\;\overrightarrow i + \left( { - 12} \right).\;\overrightarrow j \\\overrightarrow a = 8.\;\overrightarrow i + \left( { - 12} \right).\;\overrightarrow j \end{array} \right.\) nên ta suy ra \(4.\;\overrightarrow u = \overrightarrow a \)
Đúng 0
Bình luận (0)
1/ Cho tam giác ABC và trung tuyến Cm tìm và dựng điểm E sao cho :
overrightarrow{EA}+overrightarrow{EB}+2overrightarrow{EC}overrightarrow{0}
2/Cho 1 hình thang ABCD .Gọi M,N theo thứ tự là các trung điểm của các cạnh bê AD , BC . Biết overrightarrow{AB}overrightarrow{u},overrightarrow{BC}overrightarrow{v}.Hãy biểu diễn overrightarrow{NM},overrightarrow{AM},overrightarrow{CN}theo overrightarrow{u}và overrightarrow{v}
Đọc tiếp
1/ Cho tam giác ABC và trung tuyến Cm tìm và dựng điểm E sao cho :
\(\overrightarrow{EA}+\overrightarrow{EB}+2\overrightarrow{EC}=\overrightarrow{0}\)
2/Cho 1 hình thang ABCD .Gọi M,N theo thứ tự là các trung điểm của các cạnh bê AD , BC . Biết \(\overrightarrow{AB}=\overrightarrow{u},\overrightarrow{BC}=\overrightarrow{v}.\)Hãy biểu diễn \(\overrightarrow{NM},\overrightarrow{AM},\overrightarrow{CN}\)theo \(\overrightarrow{u}\)và \(\overrightarrow{v}\)
CHo hai vecto overrightarrow{u} frac{1}{2}overrightarrow{i}-5overrightarrow{i} và overrightarrow{v}koverrightarrow{i}-4overrightarrow{j}. TÌm k để vecto u và vecto v có độ dài bằng nhau
Cho 3 vecto u (4;1), v(1;4) và overrightarrow{a}overrightarrow{u}+m.overrightarrow{v} với m ∈ R. Tìm m để overrightarrow{a} vuông góc với trục hoành
Cho 2 vecto u(4;1) và v (1;4). Tìm m để vecto overrightarrow{a}m.overrightarrow{u}+overrightarrow{v} tạo với vecto overrightarrow{b}overrightarrow{i}+overrightar...
Đọc tiếp
CHo hai vecto \(\overrightarrow{u}\)= \(\frac{1}{2}\overrightarrow{i}-5\overrightarrow{i}\) và \(\overrightarrow{v}=k\overrightarrow{i}-4\overrightarrow{j}\). TÌm k để vecto u và vecto v có độ dài bằng nhau
Cho 3 vecto u = (4;1), v=(1;4) và \(\overrightarrow{a}=\overrightarrow{u}+m.\overrightarrow{v}\) với m ∈ R. Tìm m để \(\overrightarrow{a}\) vuông góc với trục hoành
Cho 2 vecto u=(4;1) và v= (1;4). Tìm m để vecto \(\overrightarrow{a}=m.\overrightarrow{u}+\overrightarrow{v}\) tạo với vecto \(\overrightarrow{b}=\overrightarrow{i}+\overrightarrow{j}\) một góc 45 độ
Cho 3 vecto overrightarrow{u}left(1;2;3right),overrightarrow{v}left(2;2-1right),overrightarrow{w}left(4;0;-4right). Tìm tọa độ của vecto overrightarrow{x}, biết
a, overrightarrow{x}overrightarrow{u}-overrightarrow{v}
b,overrightarrow{x}overrightarrow{u}-overrightarrow{v}+2overrightarrow{w}
c, overrightarrow{x}2overrightarrow{u}+4overrightarrow{v}-overrightarrow{w}
d,2overrightarrow{x}-3overrightarrow{u}overrightarrow{w}
e, 2overrightarrow{u}+overrightarrow{v}-overrightarrow{w}+3overrightarr...
Đọc tiếp
Cho 3 vecto \(\overrightarrow{u}\left(1;2;3\right),\overrightarrow{v}\left(2;2-1\right),\overrightarrow{w}\left(4;0;-4\right)\). Tìm tọa độ của vecto \(\overrightarrow{x}\), biết
a, \(\overrightarrow{x}=\overrightarrow{u}-\overrightarrow{v}\)
b,\(\overrightarrow{x}=\overrightarrow{u}-\overrightarrow{v}+2\overrightarrow{w}\)
c, \(\overrightarrow{x}=2\overrightarrow{u}+4\overrightarrow{v}-\overrightarrow{w}\)
d,\(2\overrightarrow{x}-3\overrightarrow{u}=\overrightarrow{w}\)
e, \(2\overrightarrow{u}+\overrightarrow{v}-\overrightarrow{w}+3\overrightarrow{x}=\overrightarrow{0}\)
Lời giải:
a)
\(\overrightarrow{x}=\overrightarrow{u}-\overrightarrow{v}=(1-2, 2-2,3-(-1))=(-1,0,4)\)
b)
\(\overrightarrow{x}=\overrightarrow{u}-\overrightarrow{v}+2\overrightarrow{w}=(1-2+2.4,2-2+2.0; 3-(-1)+2(-4))\)
\(=(7, 0, -4)\)
c)
\(\overrightarrow{x}=2\overrightarrow{u}+4\overrightarrow{v}-\overrightarrow{w}=(2.1+4.2-4, 2.2+4.2-0, 2.3+4.(-1)-(-4))\)
\(=(6,12,6)\)
d)
\(2\overrightarrow{x}=3\overrightarrow{u}+\overrightarrow{w}=3(1,2,3)+(4,0,-4)=(3.1+4, 3.2+0,3.3+(-4))\)
\(=(7,6,5)\Rightarrow \overrightarrow{x}=(\frac{7}{2}, 3, \frac{5}{2})\)
e)
\(3\overrightarrow{x}=-2\overrightarrow{u}-\overrightarrow{v}+\overrightarrow{w}=-2(1,2,3)-(2,2,-1)+(4,0,-4)\)
\(=(-2,-4,-6)-(2,2,-1)+(4,0,-4)=(-2-2+4,-4-2+0,-6-(-1)+(-4))\)
\(=(0,-6,-9)\Rightarrow \overrightarrow{x}=(0,-2,-3)\)
cho overrightarrow{u}left(3;-2right),overrightarrow{v}left(1;6right).khẳng điịnh nào đúng ?
A.overrightarrow{u}+overrightarrow{v},overrightarrow{a}left(-4;4right)ngược hướng B.overrightarrow{u},overrightarrow{v}cùng phương
C. overrightarrow{u}-overrightarrow{v},overrightarrow{b}left(6;-24right)cùng hướng D. 2overrightarrow{u}+overrightarrow{v},overrightarrow{v}cùng phương
Đọc tiếp
cho \(\overrightarrow{u}=\left(3;-2\right),\overrightarrow{v}=\left(1;6\right).\)khẳng điịnh nào đúng ?
A.\(\overrightarrow{u}+\overrightarrow{v},\overrightarrow{a}=\left(-4;4\right)\)ngược hướng B.\(\overrightarrow{u},\overrightarrow{v}\)cùng phương
C. \(\overrightarrow{u}-\overrightarrow{v},\overrightarrow{b}=\left(6;-24\right)\)cùng hướng D. \(2\overrightarrow{u}+\overrightarrow{v},\overrightarrow{v}\)cùng phương
1/ Cho tam giác ABC và trung tuyến CM tìm và dựng điểm E sao cho :
overrightarrow{EA}+overrightarrow{EB}+2overrightarrow{EC}overrightarrow{0}
2/Cho 1 hình thang ABCD .Gọi M,N theo thứ tự là các trung điểm của các cạnh bên AD , BC . Biết overrightarrow{AB}overrightarrow{u},overrightarrow{BC}overrightarrow{v}. Hãy biểu diễn overrightarrow{MN},overrightarrow{AM},overrightarrow{CN} theo overrightarrow{u} và overrightarrow{v}
Đọc tiếp
1/ Cho tam giác ABC và trung tuyến CM tìm và dựng điểm E sao cho :
\(\overrightarrow{EA}+\overrightarrow{EB}+2\overrightarrow{EC}=\overrightarrow{0}\)
2/Cho 1 hình thang ABCD .Gọi M,N theo thứ tự là các trung điểm của các cạnh bên AD , BC . Biết \(\overrightarrow{AB}=\overrightarrow{u},\overrightarrow{BC}=\overrightarrow{v}\). Hãy biểu diễn \(\overrightarrow{MN},\overrightarrow{AM},\overrightarrow{CN}\) theo \(\overrightarrow{u}\) và \(\overrightarrow{v}\)