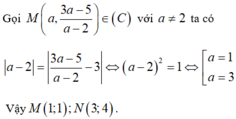tính tổng các hoành độ của những điểm thuộc đồ thị (C):Y=X^3-3X^2+2 cách đều 2 điểm A(12;1) B(-6;3)
A.2 B.0 C.4 D.3

Những câu hỏi liên quan
Bài 1: Cho hàm số y= 2x+1. Tính f(-1), f(-2), f(-1/3)
Bài 2: A và B là hai điểm thuộc đồ thị hàm số y=3x+1
a, Tung độ của điểm A bằng bao nhiêu nếu hoành độ của nó bằng 2/3?
b, Hoành độ của điểm B bằng bao nhiêu nêu tung độ của nó bằng -8?
c, Trong các điểm C(-1;2), D(2;5), E(-2;5) điểm nào thuộc đồ thị hàm số 3x+1?
Các bạn giúp mình mấy bài này nha!!!!
bài 1 : khi 2x= f( -1) thì
y= 2x + 1 = 2 nhân -1 +1
y= 2x + 1 = -1
khi 2x= f(-2 ) thì
y= 2x + 1 = 2 nhân -2 +1
y= 2x + 1 = -3
khi 2x= f(-1/3) thì
y= 2x + 1 = 2 nhân -1/3 + 1
y= 2x + 1 = 1/3
chúc bạn học tốt nha hahahah ![]()
Đúng 0
Bình luận (0)
Cho hàm số y=-2/3x a) ve đồ thị hàm số b) xác định tọa độ điểm có hoành độ là 5 và điểm có tung độ bằng -2/7 thuộc đồ thị hàm số c) Điểm C(-1;2/3);D(-1;-2/3) điểm nào thuộc đồ thị hàm số
b: \(\left(5;-\dfrac{10}{3}\right);\left(\dfrac{3}{7};-\dfrac{2}{7}\right)\)
Đúng 0
Bình luận (0)
Cho hàm số :
ydfrac{3}{4}x^2
a) Vẽ đồ thị của hàm số
b) Tìm trên đồ thị điểm A có hoành độ bằng -2. Bằng đồ thị, tìm tung độ của A
c) Tìm trên đồ thị các điểm có tung độ bằng 4. Tính gần đúng (làm tròn đến chữ số thập phân thứ nhất) hoành độ của những điểm này bằng hai cách :
- Ước lượng trên đồ thị
- Tính theo công thức ydfrac{3}{4}x^2
Đọc tiếp
Cho hàm số :
\(y=\dfrac{3}{4}x^2\)
a) Vẽ đồ thị của hàm số
b) Tìm trên đồ thị điểm A có hoành độ bằng -2. Bằng đồ thị, tìm tung độ của A
c) Tìm trên đồ thị các điểm có tung độ bằng 4. Tính gần đúng (làm tròn đến chữ số thập phân thứ nhất) hoành độ của những điểm này bằng hai cách :
- Ước lượng trên đồ thị
- Tính theo công thức \(y=\dfrac{3}{4}x^2\)
b: Thay x=-2 vào (P), ta được:
\(y=\dfrac{3}{4}\cdot\left(-2\right)^2=3\)
c: Thay y=4 vào (P), ta được:
\(\dfrac{3}{4}x^2=4\)
=>x2=16/3
hay \(x\in\left\{2,3;-2,3\right\}\)
Đúng 0
Bình luận (0)
a,Vẽ đồ thị hàm số:y=-3x,y=2/3x trên cùng một hệ tọa độ Oxy
b,Điểm M(2;2/3),N(6;4).Điểm nào thuộc và không thuộc đồ thị hàm số: y=2/3x
c,Đánh dấu trên đồ thị hàm số y=-3x điểm có hoành độ bằng -1,5
d,Đánh dấu trên đồ thị hàm số y=2/3x điểm có tung độ bằng 1
b: Điểm N thuộc, điểm M ko thuộc
Đúng 0
Bình luận (0)
Tìm tọa độ điểm M có hoành độ dương thuộc đồ thị (C) của hàm số
y
x
+
2
x
−
2
sao cho tổng khoảng cách từ M đến hai đường tiệm cận của đồ thị (C) đạt giá trị nhỏ nhất. A. M(1;-3) B. M(3;5) C. M(0;-1) D. M(4;3)
Đọc tiếp
Tìm tọa độ điểm M có hoành độ dương thuộc đồ thị (C) của hàm số y = x + 2 x − 2 sao cho tổng khoảng cách từ M đến hai đường tiệm cận của đồ thị (C) đạt giá trị nhỏ nhất.
A. M(1;-3)
B. M(3;5)
C. M(0;-1)
D. M(4;3)
Đáp án là D

Dấu “ = ” xảy ra ó
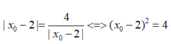
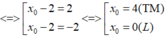
Vậy M(4;3)
Đúng 0
Bình luận (0)
GIÚP MÌNH GẤP VỚI Ạ, PLS.
a) Vẽ đồ thị hàm số y=3x-3.
b) Xác định hàm số y=3x-1+a, biết đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 3.
c) Tìm tọa độ giao điểm của 2 đồ thị hàm số của câu a) và b) bằng phép tính.
\(b,\Leftrightarrow x=3;y=0\Leftrightarrow9-1+a=0\Leftrightarrow a=-8\\ \Leftrightarrow y=3x-1-8=3x-9\\ c,\text{PT hoành độ giao điểm: }3x-3=3x-9\Leftrightarrow0x=-6\Leftrightarrow x\in\varnothing\)
Vậy 2 đt trên không cắt nhau
Đúng 0
Bình luận (1)
Cho hàm số \(y = - 2{x^2}\).
a) Điểm nào trong các điểm có tọa độ \(\left( { - 1; - 2} \right),\left( {0;0} \right),\left( {0;1} \right),\left( {2021;1} \right)\) thuộc đồ thị của hàm số trên?
b) Tìm những điểm thuộc đồ thị hàm số có hoành độ lần lượt bằng \( - 2;3\) và 10.
c) Tìm những điểm thuộc đồ thị hàm số có tung độ bằng \( - 18\).
a)
+) Thay tọa độ \(\left( { - 1; - 2} \right)\) vào hàm số \(y = - 2{x^2}\) ta được:
\( - 2 = - 2.{\left( { - 1} \right)^2}\)(Đúng)
=> \(\left( { - 1; - 2} \right)\) thuộc đồ thị hàm số \(y = - 2{x^2}\).
+) Thay tọa độ \(\left( {0;0} \right)\) vào hàm số \(y = - 2{x^2}\) ta được:
\(0 = - {2.0^2}\)(Đúng)
=> \(\left( {0;0} \right)\) thuộc đồ thị hàm số \(y = - 2{x^2}\).
+) Thay tọa độ \(\left( {0;1} \right)\) vào hàm số \(y = - 2{x^2}\) ta được:
\(1 = - {2.0^2} \Leftrightarrow 1 = 0\)(Vô lí)
=> \(\left( {0;1} \right)\) không thuộc đồ thị hàm số \(y = - 2{x^2}\).
+) Thay tọa độ \(\left( {2021;1} \right)\) vào hàm số \(y = - 2{x^2}\) ta được:
\(1 = - {2.2021^2}\)(Vô lí)
=> \(\left( {2021;1} \right)\) không thuộc đồ thị hàm số \(y = - 2{x^2}\).
b)
+) Thay \(x = - 2\) vào hàm số \(y = - 2{x^2}\) ta được:
\(y = - 2.{\left( { - 2} \right)^2} = - 8\)
+) Thay \(x = 3\) vào hàm số \(y = - 2{x^2}\) ta được:
\(y = - {2.3^2} = - 18\)
+) Thay \(x = 10\) vào hàm số \(y = - 2{x^2}\) ta được:
\(y = - 2.{\left( {10} \right)^2} = - 200\)
c) Thay \(y = - 18\) vào hàm số \(y = - 2{x^2}\) ta được:
\( - 18 = - 2{x^2} \Leftrightarrow {x^2} = 9 \Leftrightarrow x = \pm 3\)
Vậy các điểm có tọa độ (3;-18) và (-3;-18) thuộc đồ thị hàm số có tung độ bằng -18.
Đúng 0
Bình luận (0)
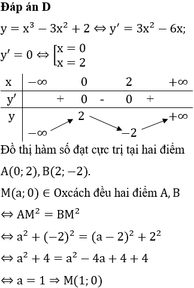
Tìm tất cả những điểm thuộc trục hoành cách đều hai điểm cực trị của đồ thị hàm số y = x 3 - 3 x 2 + 2 .
A. M(-1; 0)
B. M(-1; 0), O(0; 0)
C. M(2; 0)
D. M(1; 0)
Tọa độ các điểm thuộc đồ thị (C) của hàm số y
3
x
-
5
x
-
2
cách đều hai tiệm cận của (C). A. B. C. D.
Đọc tiếp
Tọa độ các điểm thuộc đồ thị (C) của hàm số y = 3 x - 5 x - 2 cách đều hai tiệm cận của (C).
A. ![]()
B. ![]()
C.![]()
D.![]()