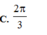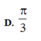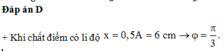2sin(x+10độ) - √12cos(x+10 độ)=3

Những câu hỏi liên quan
Cho tan alpha =3
Tính P= 3cos(alpha) - 2sin(alpha)
12cos^3(alpha) +4sin^3 (alpha)
tính các góc của tam giác abc biết
a) 3 x a = 4 x b và a - b = 20độ
b) b - c = 10độ và c - a = 10 độ
a) Có: 3 . \(\widehat{A}\) = 4 . \(\widehat{B}\)
=> \(\frac{\widehat{A}}{4}\) = \(\frac{\widehat{B}}{3}\) và \(\widehat{A}-\widehat{B}=20^o\)
Áp dugj tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{\widehat{A}}{4}\) = \(\frac{\widehat{B}}{3}\) = \(\frac{\widehat{A}-\widehat{B}}{4-3}\) = \(\frac{20}{1}\) = 20
\(\Rightarrow\) \(\left[\begin{array}{nghiempt}\widehat{A}=20.4\\\widehat{B}=20.3\\\widehat{C}=180-\left(20.4+20.3\right)\end{array}\right.\) \(\Rightarrow\) \(\left[\begin{array}{nghiempt}\widehat{A}=80^o\\\widehat{B}=60^o\\\widehat{C}=40^o\end{array}\right.\)
Vậy 3 góc của ΔABC lần lượt có số đo là: 80o ; 60o; 40o
Đúng 0
Bình luận (0)
a) 2sinleft(x+dfrac{pi}{3}right)+10b) 1+2sinleft(x-30^oright)0c) sqrt{3}+2sinleft(x-dfrac{pi}{6}right)0d) 2sinleft(x+10^oright)+sqrt{3}0e) sqrt{2}+2sinleft(x-15^oright)0f) sqrt{2}sinleft(x-dfrac{pi}{3}right)+10g) 3+sqrt{5}sinleft(x+dfrac{pi}{3}right)0h) 1+sinleft(x-30^oright)0i) 3+sqrt{5}sinleft(x-dfrac{pi}{6}right)0k) 2sqrt{2}sin^2x-sin2x0
Đọc tiếp
a) \(2sin\left(x+\dfrac{\pi}{3}\right)+1=0\)
b) \(1+2sin\left(x-30^o\right)=0\)
c) \(\sqrt{3}+2sin\left(x-\dfrac{\pi}{6}\right)=0\)
d) \(2sin\left(x+10^o\right)+\sqrt{3}=0\)
e) \(\sqrt{2}+2sin\left(x-15^o\right)=0\)
f) \(\sqrt{2}sin\left(x-\dfrac{\pi}{3}\right)+1=0\)
g) \(3+\sqrt{5}sin\left(x+\dfrac{\pi}{3}\right)=0\)
h) \(1+sin\left(x-30^o\right)=0\)
i) \(3+\sqrt{5}sin\left(x-\dfrac{\pi}{6}\right)=0\)
k) \(2\sqrt{2}sin^2x-sin2x=0\)
a: =>2sin(x+pi/3)=-1
=>sin(x+pi/3)=-1/2
=>x+pi/3=-pi/6+k2pi hoặc x+pi/3=7/6pi+k2pi
=>x=-1/2pi+k2pi hoặc x=2/3pi+k2pi
b: =>2sin(x-30 độ)=-1
=>sin(x-30 độ)=-1/2
=>x-30 độ=-30 độ+k*360 độ hoặc x-30 độ=180 độ+30 độ+k*360 độ
=>x=k*360 độ hoặc x=240 độ+k*360 độ
c: =>2sin(x-pi/6)=-căn 3
=>sin(x-pi/6)=-căn 3/2
=>x-pi/6=-pi/3+k2pi hoặc x-pi/6=4/3pi+k2pi
=>x=-1/6pi+k2pi hoặc x=3/2pi+k2pi
d: =>2sin(x+10 độ)=-căn 3
=>sin(x+10 độ)=-căn 3/2
=>x+10 độ=-60 độ+k*360 độ hoặc x+10 độ=240 độ+k*360 độ
=>x=-70 độ+k*360 độ hoặc x=230 độ+k*360 độ
e: \(\Leftrightarrow2\cdot sin\left(x-15^0\right)=-\sqrt{2}\)
=>\(sin\left(x-15^0\right)=-\dfrac{\sqrt{2}}{2}\)
=>x-15 độ=-45 độ+k*360 độ hoặc x-15 độ=225 độ+k*360 độ
=>x=-30 độ+k*360 độ hoặc x=240 độ+k*360 độ
f: \(\Leftrightarrow sin\left(x-\dfrac{pi}{3}\right)=-\dfrac{1}{\sqrt{2}}\)
=>x-pi/3=-pi/4+k2pi hoặc x-pi/3=5/4pi+k2pi
=>x=pi/12+k2pi hoặc x=19/12pi+k2pi
Đúng 1
Bình luận (0)
g) \(3+\sqrt[]{5}sin\left(x+\dfrac{\pi}{3}\right)=0\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{3}\right)=-\dfrac{3}{\sqrt[]{5}}\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{3}\right)=sin\left[arcsin\left(-\dfrac{3}{\sqrt[]{5}}\right)\right]\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{3}=arcsin\left(-\dfrac{3}{\sqrt[]{5}}\right)+k2\pi\\x+\dfrac{\pi}{3}=\pi-arcsin\left(-\dfrac{3}{\sqrt[]{5}}\right)+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=arcsin\left(-\dfrac{3}{\sqrt[]{5}}\right)-\dfrac{\pi}{3}+k2\pi\\x=\dfrac{2\pi}{3}-arcsin\left(-\dfrac{3}{\sqrt[]{5}}\right)+k2\pi\end{matrix}\right.\)
h) \(1+sin\left(x-30^o\right)=0\)
\(\Leftrightarrow sin\left(x-30^o\right)=-1\)
\(\Leftrightarrow sin\left(x-30^o\right)=sin\left(-90^o\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x-30^o=-90^0+k360^o\\x-30^o=180^o+90^0+k360^o\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-60^0+k360^o\\x=300^0+k360^o\end{matrix}\right.\)
\(\Leftrightarrow x=-60^0+k360^o\)
Đúng 1
Bình luận (0)
Một vật nhỏ dao động điều hòa dọc theo trục Ox có phương trình dao động là x = 12cos(2πt + π/3) cm. Biên độ dao động của vật là
A. 6 cm
B. 6 2 cm
C. 3 cm
D. 12 cm
Biên độ dao động của vật A = 12cm
Đáp án D
Đúng 0
Bình luận (0)
Một vật nhỏ dao động điều hòa dọc theo trục Ox có phương trình dao động là x = 12cos(2πt + π/3) cm. Biên độ dao động của vật là
A. 2π cm.
B. 6 cm.
C. π/3 cm.
D. 12 cm
Đáp án D
+ Biên độ dao động của vật A=12cm
Đúng 0
Bình luận (0)
Ba dao động điều hoà giống nhau đc treo cùng độ cao và cách đều nhau.hai con lắc ở hai bên có pt x1=12căn3cos(pit+2pi/3)cm và x=12cos(pit+pi/6).để ba vật nhỏ gắn ở ba lò xo lluoon thẳng hàng thì con lắc ở giữa phải có pt
A.x2=24cos(pit+pi/2)
B.12cos(pit+5pi/6)
C.12cos(pit+5pi/6)
D.24cos(pit+5pi/6)
Để 3 vật nhỏ luôn thẳng hàng thì: x2 = (x1 + x3) / 2.
\(\Rightarrow x_2=\frac{24\cos\left(\pi t+\frac{\pi}{2}\right)}{2}=12\cos\left(\pi t+\frac{\pi}{2}\right)\)
Đúng 0
Bình luận (0)
Có thể giải thích rõ hơn k? Vì mình cũng đag thắc mắc câu hỏi này. Cám ơn
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Một vật nhỏ dao động điều hòa dọc theo trục Ox có phương trình dao động là x=12cos(2πt+π/3) cm. Biên độ dao động của vật có giá trị là
A. 6 cm.
B. 2π cm.
C. π/3 cm.
D. 12 cm.
Đáp án D
Phương pháp: Sử dụng lí thuyết về phương trình dao động điều hoà
PT dao động x = 12cos(2πt + π/3) cm => Biên độ dao động A = 12cm
Đúng 0
Bình luận (0)
1) 2sin(x+10\(^o\)) - \(\sqrt{12}\)cos(x+10\(^o\))=3
2) \(\sqrt{3}\)sin4x - cos4x =\(\sqrt{3}\)
3) sin2x - cot \(\dfrac{pi}{5}\).cos2x=1
4) cos x -\(\sqrt{3}\) sinx = -2cos3x
1.
\(2sin\left(x+10^o\right)-\sqrt{12}cos\left(x+10^o\right)=3\)
\(\Leftrightarrow\dfrac{1}{2}sin\left(x+10^o\right)-\dfrac{\sqrt{3}}{2}cos\left(x+10^o\right)=\dfrac{3}{4}\)
\(\Leftrightarrow sin\left(x+50^o\right)=\dfrac{3}{4}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+50^o=arcsin\left(\dfrac{3}{4}\right)+k360^o\\x+50^o=180^o-arcsin\left(\dfrac{3}{4}\right)+k360^o\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-50^o+arcsin\left(\dfrac{3}{4}\right)+k360^o\\x=130^o-arcsin\left(\dfrac{3}{4}\right)+k360^o\end{matrix}\right.\)
Đúng 0
Bình luận (0)
2.
\(\sqrt{3}sin4x-cos4x=\sqrt{3}\)
\(\Leftrightarrow\dfrac{\sqrt{3}}{2}sin4x-\dfrac{1}{2}cos4x=\dfrac{\sqrt{3}}{2}\)
\(\Leftrightarrow sin\left(4x-\dfrac{\pi}{3}\right)=\dfrac{\sqrt{3}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}4x-\dfrac{\pi}{3}=\dfrac{\pi}{3}+k2\pi\\4x-\dfrac{\pi}{3}=\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2\pi}{12}+\dfrac{k\pi}{2}\\x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
3.
\(sin2x-cot\dfrac{\pi}{5}.cos2x=1\)
\(\Leftrightarrow\sqrt{1+cot\dfrac{\pi}{5}}\left(\dfrac{1}{\sqrt{1+cot\dfrac{\pi}{5}}}sin2x-\dfrac{cot\dfrac{\pi}{5}}{\sqrt{1+cot\dfrac{\pi}{5}}}.cos2x\right)=1\)
\(\Leftrightarrow sin\left[2x-arccos\left(\dfrac{1}{\sqrt{1+cot\dfrac{\pi}{5}}}\right)\right]=\dfrac{1}{\sqrt{1+cot\dfrac{\pi}{5}}}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-arccos\left(\dfrac{1}{\sqrt{1+cot\dfrac{\pi}{5}}}\right)=arcsin\left(\dfrac{1}{\sqrt{1+cot\dfrac{\pi}{5}}}\right)+k2\pi\\2x-arccos\left(\dfrac{1}{\sqrt{1+cot\dfrac{\pi}{5}}}\right)=\pi-arcsin\left(\dfrac{1}{\sqrt{1+cot\dfrac{\pi}{5}}}\right)+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}arccos\left(\dfrac{1}{\sqrt{1+cot\dfrac{\pi}{5}}}\right)+\dfrac{1}{2}arcsin\left(\dfrac{1}{\sqrt{1+cot\dfrac{\pi}{5}}}\right)+k\pi\\x=\dfrac{\pi}{2}+\dfrac{1}{2}arccos\left(\dfrac{1}{\sqrt{1+cot\dfrac{\pi}{5}}}\right)-\dfrac{1}{2}arcsin\left(\dfrac{1}{\sqrt{1+cot\dfrac{\pi}{5}}}\right)+k\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Chất điểm dao động điều hòa với phương trình
x
12
cos
(
10
t
-
π
6
)
c
m
. Khi li độ của chất điểm bằng 6cm thì pha dao động bằng bao nhiêu?
Đọc tiếp
Chất điểm dao động điều hòa với phương trình x = 12 cos ( 10 t - π 6 ) c m . Khi li độ của chất điểm bằng 6cm thì pha dao động bằng bao nhiêu?
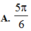
![]()