Giúp mình với!
Cho hình chóp tam giác đều SABC có mặt bên là những tam giác, AB=4cm, O là trọng tâm, M là trung điểm BC
a) Tính độ dài SO,SM
b) Tính Sxq, Stp, Vhình chóp.
![]()
Cho hình chóp tam giác đều S.ABC. Gọi M là trung điểm BC, G là trọng tâm tam giác ABC, AB = 2a; góc giữa mặt bên và đáy bằng 60.
a/ Tính thể tích chóp S.ABC
b/ Tính khoảng cách giữa SA và BC
Cho hình chóp SABC có SA vuông với đáy. SA=2a, tam giác ABC đều có cạnh bằng 4a. Mà M là trung điểm BC
a) CMR: BC vuông với (SAM)
b) Tính d(A;(SBC))
c) Gọi G là trọng tâm tam giác SAB. Tính d(G;(SBC))
a: BC vuông góc AM
BC vuông góc SA
=>BC vuông góc (SAM)
b: Kẻ AK vuông góc SM
=>AK=d(A;(SBC))
AM=4a*căn 3/2=2a*căn 3
=>SM=4a
=>AK=2a*2a*căn 3/4a=a*căn 3
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, SO vuông góc với mặt phẳng đáy, mặt bên (SAB) là tam giác đều cạnh a và hợp với đáy 1 góc 450. Gọi M, N lần lượt là trung điểm của AB và AD. Tính thể tích khối chóp S.ABCD và khoảng cách giữa SM và NC
❤sin45=\(\dfrac{SO}{SM}\) => SO=sin45 . SM= \(\dfrac{\sqrt{2}}{2}.\dfrac{a\sqrt{3}}{2}\) = \(\dfrac{a\sqrt{6}}{4}\)
OM= \(\sqrt{SM^2-SO^2}\) = \(\dfrac{a\sqrt{6}}{4}\)
BC = 2OM => BC=\(\dfrac{a\sqrt{6}}{2}\)
V = \(\dfrac{1}{3}.AB.BC.SO=\dfrac{1}{3}.a.\dfrac{a\sqrt{6}}{2}.\dfrac{a\sqrt{6}}{4}=\dfrac{a^3}{4}\)
❤ta có: SM⊂ (SAB) (1)
mà: \(\left\{{}\begin{matrix}NC//AB\\AB\subset\left(SAB\right)\end{matrix}\right.\) => NC// (SAB) (2)
từ (1) và (2) => SM//NC
\(d_{\left(SM,NC\right)}=d_{\left(NC,\left(SAB\right)\right)}=d_{\left(N,\left(SAB\right)\right)}=2d_{\left(O,\left(SAB\right)\right)}\)
+kẻ OH⊥SM
+ Ta có: \(\left\{{}\begin{matrix}AB\perp OM\\AB\perp SO\end{matrix}\right.\) => AB ⊥ (SOM) \(\supset OH\)
=> \(\left\{{}\begin{matrix}OH\perp AB\\OH\perp SM\end{matrix}\right.\) => OH⊥(SAB)
➜d(O,(SAB)) =OH
OH=\(\dfrac{OM.SO}{\sqrt{OM^2+SO^2}}\)\(\dfrac{a\sqrt{3}}{4}\)
➜d(N,(SAB)) =d(SM,NC)= \(\dfrac{a\sqrt{3}}{2}\)
Hình chóp tứ giác đều S.ABCD có các mặt bên là những tam giác đều AB =8cm,O là trung điểm của AC.Độ dài đoạn SO là:
A.82 m
B.6m
C.32 m
D.4m
Kết quả nào đúng?
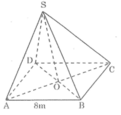
Đáy ABCD là hình vuông nên △ OAB vuông cân tại O.
Áp dụng định lí pi-ta-go ta tính được OA bằng 32
Ta có: SO ⊥ OA nên tam giác AOA cân tại O.
Áp dụng Pi-ta-go vào tam giác vuông SOA ta tỉnh được SO bằng 32
Vậy chọn đáp án C.
Cho hình chóp SABC có các mặt là tam giác đều cạnh a.Gọi M là trung điểm của SA. N là trung điểm của BC. a) chứng minh MN vuông góc SA và BC b) tính thể tích hình chóp SABC theo a
cho hình chóp SABC có đáy ABC là tam giác vuông tại B. góc ABC bằng 120 độ. AB=a . SB vuông góc với mặt đáy .goc giữa mặt phẳng SAC và mặt phẳng ABC bằng 45 .M là trung điểm của AC N là trung điểm của SM. tính theo a thể tích hình chóp va khoảng cách từ C đến mặt phẳng ABN
Cho hình chóp ngũ giác đều S.ABCDE.
a) Hình chóp có bao nhiêu cạnh và bao nhiêu đỉnh?
b) Hình chóp có bao nhiêu mặt là các tam giác cân?
c) Trong (SDE) kẻ đường SM với M là trung điểm DE. Hỏi SM là đường gì của tam giác SDE và là đường gì cùa hình chóp đều?
a) Có 10 cạnh có 6 đỉnh.
b) Có 5 mặt là các tam giác cân.
c) SM là đường cao của tam giác SDE đồng thời là trung đoạn của hình chóp
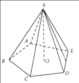
Hình chóp tam giác đều SABC có đáy là tam giác đều ABC, AB = a; góc giữa cạnh bên và mặt đáy bằng 45°. Tính thể tích V của hình chóp.
A. V = a 3 12
B. V = a 3 2 24
C. V = a 3 3 16
D. V = a 3 6 36
Cho hình chóp Sabc. GỌI h,k là trọng tâm của tam giác SAB, SBC, M là trung điểm của AC. I thuộc SM, SI>IM. Tìm (IHM) và (SBC) Giúp em tìm giao tuyến hai mặt phẳng này vs
Cho hình chóp tam giác đều SABC có đáy ABC là tam giác đều cạnh a tâm đường tròn ngoại tiếp tam giác ABC là O. Biết SO=2a. Tính diện tích xung quanh và thể tích hình chóp theo a.