Let ABCD.A'B'C'D' be a cube with AC'= \(\sqrt{3}\) Find the total are of this cube
(cho hình lập phương ABCD.A'B'C'D' với AC'=\(\sqrt{3}\). tìm diện tích toàn phần của hình lập phương đó)
Hình lăng trụ đứng. Hình chóp đều.
Hỏi đáp
Bài 1: Hình hộp chữ nhật
Bài 2: Hình hộp chữ nhật (Tiếp)
Bài 3: Thể tích hình hộp chữ nhật
Bài 4: Hình lăng trụ đứng
Bài 5: Diện tích xung quanh của hình lăng trụ đứng
Bài 6: Thể tích của hình lăng trụ đứng
Bài 7: Hình chóp đều và hình chóp cụt đều
Bài 8: Diện tích xung quanh của hình chóp đều
Bài 9: Thể tích hình chóp đều
Ôn tập chương Hình lăng trụ đứng. Hình chóp đều.
bai 3,4 sgk toan 8 trang 97
Bài 3:
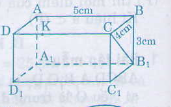
Vì ABCD. A 1B1C1D1 là hình hộp chữ nhật nên DCC1D1; CB1C1 là hình chữ nhật
∆DCC1 vuông tại C
=> =
=
(cm)
∆CBB1 vuông tại B
=> =
=
= 5(cm)
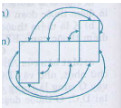
Bài 4:
Ta điền thêm vào hình vẽ sau các mũi tên để có được một hình lập phương.
Đúng 0
Bình luận (0)
Một bể đựng nước có dạng hình hộp chữ nhật có diện tích đáy ( phía trong bể ) là 1,8m2 .Lúc đầu bể không có nước, người ta đổ vào bể 30 thùng nước mỗi thùng 24 lít.Tính chiều cao mực nước trong bể
Cho hình thang cân ABCD (AB//CD) ,biết AB=8cm, AD=5cm, CD=16cm. Tính diện tích hình thang ABCD
Kẻ AE , BF vuông góc với DC (1)
mà AB//DC
suy ra: AE, BF vuông góc AB (2)
Từ (1) và (2) suy ra:
ABCD là hình chữ nhật => AB=EF=8cm
Xét tam giác ADE và tam giác BCF, ta có:
Ê = F^
D^=C^
AD=BC
=> tam giác ADE = tam giác BCF (ch-gn)
=>DE=FC
mà DE+FC+EF=CD
hay 2DE +8 =16
<=>2DE =8
<=>DE=4(cm)
Xét tam giác ADE vuông tại Ê ta có:
AD2 = DE2 + AE2
hay 52 = 42 + AE2
<=> AE= 3 (cm)
Diện tích hình thang ABCD là
SABCD = (AB+CD).AE:2=(8+16).3:2=36(cm2 )
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD có AB=12cm, BC=9cm.Gọi H là chân đường vuông góc kẻ từ A xuống BD.
a/ Chứng minh: tam giác AHB đồng dạng với tam giác BCD.
b/ Tính độ dài đoạn thẳng AH.
a: Xét ΔAHB vuông tại H và ΔBCD vuông tại C có
\(\widehat{ABH}=\widehat{BDC}\)
Do đó: ΔAHB\(\sim\)ΔBCD
b: \(BD=\sqrt{12^2+9^2}=15\left(cm\right)\)
\(AH=\dfrac{12\cdot9}{15}=7.2\left(cm\right)\)
Đúng 0
Bình luận (0)
Giúp mình với!
Cho hình chóp tam giác đều SABC có mặt bên là những tam giác, AB=4cm, O là trọng tâm, M là trung điểm BC
a) Tính độ dài SO,SM
b) Tính Sxq, Stp, Vhình chóp.
![]()
Hình chữ nhật ABCD , M ,N lần lượt là trung điểm của AB và CD. E là giao điểm của AN và DM , F là giao điểm của CM và BN. AC cắt DM, MN,BN lần lượt tại H , O , K
a, chứng minh AMND . BMNC là hình chữ nhật.
c, EMFN là hình thoi
d, AH = HK = KC
e, E,O,F thẳng hàng
GIÚP MÌNH VS MN!..............................
a: Xét tứ giác AMND có
AM//ND
AM=ND
Do đó: AMND là hình bình hành
mà \(\widehat{MAD}=90^0\)
nên AMND là hình chữ nhật
Xét tứ giác BMNC có
BM//NC
BM=NC
Do đó: BMNC là hình bình hành
mà \(\widehat{MBC}=90^0\)
nên BMNC là hình chữ nhật
c: Xét tứ giác BMDN có
BM//DN
BM=DN
Do đó: BMDN là hình bình hành
Suy ra: DM//BN
hay EM//FN
Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
SUy ra: AN//CM
hay EN//MF
Ta có: AMND là hình chữ nhật
nên Hai đường chéo AN và MD cắt nhau tại trung điểm của mỗi đường và AN=MD
=>EM=EN
Xét tứ giác EMFN có
EM//FN
MF//EN
Do đó: EMFN là hình bình hành
mà EM=EN
nên EMFN là hình thoi
Đúng 0
Bình luận (0)
d: Xét ΔHCD có
N là trung điểm của DC
NK//HD
DO đó: K là trung điểm của HC
=>KC=KH(1)
Xét ΔABK có
M là trung điểm của AB
MH//BK
Do đó: H là trung điểm của AK
=>AH=HK(2)
Từ(1) và (2) suy ra AH=HK=KC
e: Ta có: AMCN là hình bình hành
nên Hai đường chéo AC và MN cắt nhau tại trung điểm của mỗi đường
=>O là trung điểm của MN
Ta có: EMFN là hình thoi
nên hai đường chéo FE và MN cắt nhau tại trung điểm của mỗi đường
=>O là trung điểm của EF
hay E,O,F thẳng hàng
Đúng 0
Bình luận (0)
Cho hình lăng trụ đứng ABCD . A'B'C'D' có đáy là hình thoi. Biết đường AA'=5; đường chéo AC'=15; DB'=9. Tính cạnh AB của đáy.
Tam giác ABC ,AB= 6cm ,AC=9cm, BC =12cm .Phân giác BF , FE// BC .M là trung điểm của BC , AM cắt EF tại K và cắt BF tại H
aTính FA, EF
b,C/m KE=KF
c.C/m E,H,C thẳng hàng
lăng trụ tam giác đều ABC.A'B'C' cạnh đáy =a, cạnh bên =a\(\sqrt{2}\). M,N thuộc AB' và A'C sao cho \(\dfrac{AM}{AB'}=\dfrac{A'N}{A'C}=\dfrac{1}{3}\). tính thể tích BMNC'C











