Lập phương trình mặt phẳng (O) song song và cách đều hai mặt phẳng
\(\left(P_1\right):2x+y+2z+1=0\)
\(\left(P_2\right):2x+y+2z+5=0\)
Những câu hỏi liên quan
Lập phương trình mặt phẳng (P) song song và cách đều hai mặt phẳng
( P 1 ): 2x + y + 2z + 1 = 0 và ( P 2 ): 2x + y + 2z + 5 = 0.
Ta có: M(x, y, z) ∈ (P)
⇔ d(M, ( P 1 )) = d(M, ( P 2 ))
⇔|2x + y + 2z + 1| = |2x + y + 2z + 5|
⇔ 2x + y + 2z + 1 = – (2x + y + 2z + 5)
⇔ 2x + y + 2z + 3 = 0
Từ đó suy ra phương trình của (P) là: 2x + y + 2z + 3 = 0.
Đúng 0
Bình luận (0)
Cho hai mặt phẳng
\(\left(P_1\right):2x+y+z+1=0\)
\(\left(P_2\right):4x-2y-4z+7=0\)
Lập phương trình mặt phẳng sao cho khoảng cách từ mỗi điểm của nó đến \(\left(P_1\right)\&\left(P_2\right)\) là bằng nhau
Tính khoảng cách h giữa hai mặt phẳng song song:
P
:
2
x
-
y
+
2
z
-
1
0
và
Q
:
2
x
-
y
+
2
z
+
1
0
.
Đọc tiếp
Tính khoảng cách h giữa hai mặt phẳng song song: P : 2 x - y + 2 z - 1 = 0 và Q : 2 x - y + 2 z + 1 = 0 .
Trong không gian Oxyz, lập phương trình mặt phẳng (P) đi qua điểm A(2;-1;-2) và song song với mặt phẳng (Q): 2x - y + 2z 0 A. 2x - y + 2z - 1 0 B. 2x - y + 2z + 9 0 C. 2x - y - 2z + 1 0 D. 2x - y + 2z + 1 0
Đọc tiếp
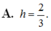
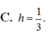
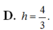
Trong không gian Oxyz, lập phương trình mặt phẳng (P) đi qua điểm A(2;-1;-2) và song song với mặt phẳng (Q): 2x - y + 2z = 0
A. 2x - y + 2z - 1 = 0
B. 2x - y + 2z + 9 = 0
C. 2x - y - 2z + 1 = 0
D. 2x - y + 2z + 1 = 0
Đáp án A
Vì mặt phẳng (P) song song với mặt phẳng (Q): 2x – y + 2z = 0 nên mặt phẳng (P) có dạng: 2x – y + 2z + d = 0
Mà mặt phẳng (P) đi qua điểm A(2; -1; -2) nên:
2.2 –(-1) + 2.(-2) + d = 0 nên d = -1
Vậy phương trình mặt phẳng (P) là: 2x – y + 2z – 1= 0
Đúng 0
Bình luận (0)
Hãy viết phương trình mặt phẳng \(\left(\alpha\right)\) đi qua gốc tọa độ \(O\left(0;0;0\right)\) và song song với mặt phẳng \(\left(\beta\right):x+y+2z-7=0\) ?
Phương trình mặt phẳng qua giao tuyến của hai mặt phẳng (P)x-3y+2z-1=0 và (Q)2x+y-3z+1=0 và song song với trục Ox là
Chọn \(M\left(-5;0;3\right)\) là điểm nằm trên giao tuyến của (P) và (Q)
\(\overrightarrow{n_P}=\left(1;-3;2\right)\) ; \(\overrightarrow{n_Q}=\left(2;1;-3\right)\)
\(\Rightarrow7\overrightarrow{u}=\left[\overrightarrow{n_P};\overrightarrow{n_Q}\right]=7\left(1;1;1\right)\)
Trục Ox có 1 vtcp là \(\overrightarrow{u_1}=\left(1;0;0\right)\)
\(\left[\overrightarrow{u};\overrightarrow{u_1}\right]=\left(0;1;-1\right)\)
Phương trình mặt phẳng cần tìm có dạng:
\(y-1\left(z-3\right)=0\Leftrightarrow y-z+3=0\)
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho mặt cầu
S
:
x
2
+
y
2
+
z
2
+
2
x
−
4
y
−
6
z
+
5
0
. Mặt phẳng tiếp xúc với (S) và song song với mặt phẳng
P
:
2
x
−
y
+
2
z...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu S : x 2 + y 2 + z 2 + 2 x − 4 y − 6 z + 5 = 0 . Mặt phẳng tiếp xúc với (S) và song song với mặt phẳng P : 2 x − y + 2 z − 11 = 0 có phương trình là:
A. 2 x − y + 2 z − 7 = 0
B. 2 x − y + 2 z + 9 = 0
C. 2 x − y + 2 z + 7 = 0
D. 2 x − y + 2 z − 9 = 0
Phương pháp:
Mặt phẳng (Q) song song với mặt phẳng
Đúng 0
Bình luận (0)
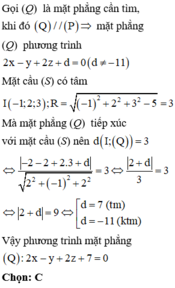
Trong không gian với hệ tọa độ Oxyz cho 2 điểm A(1;0;1) và B(-1;1;0), mặt phẳng (P):\(x+y-2z-5=0\) và mặt cầu \(\left(S\right):x^2+y^2+z^2-2x+2y-6=0\).
Viết phương trình mặt phẳng (Q), biết (Q) vuông góc với (P), song song với đường thẳng AB và tiếp xúc với mặt cầu (S)
Mặt phẳng (P) có vec tơ pháp tuyến \(\overrightarrow{n}=\left(1;1;-2\right);\overrightarrow{AB}=\left(-2;1;-1\right)\)
Ta có \(\left[\overrightarrow{n};\overrightarrow{AB}\right]=\left(1;5;3\right)\)
(Q) vuông góc với (P), song song với đường thẳng AB suy ra (Q) có vectơ pháp tuyến là \(\left[\overrightarrow{n_1};\overrightarrow{AB}\right]=\left(1;5;3\right)\) nên phương trình mặt phẳng (Q) có dạng \(x+5y+3z+m=0\)
Mặt cầu (S) có tâm \(I\left(1;-1;1\right)\), bán kính R = 3
Mặt phẳng (Q) tiếp xúc với (S) có \(d\left(I,\left(Q\right)\right)=R\Leftrightarrow\frac{\left|1-5+3+m\right|}{\sqrt{35}}\)
\(\Leftrightarrow\left|m-1\right|=3\sqrt{35}\Leftrightarrow\begin{cases}m=1+3\sqrt{35}\\m=1-3\sqrt{35}\end{cases}\)
- Với \(m=1+3\sqrt{35}\) ta có phương trình mặt phẳng (Q) là : \(x+5y+3z+1+3\sqrt{35}=0\)
- Với \(m=1-3\sqrt{35}\) ta có phương trình mặt phẳng (Q) là : \(x+5y+3z+1-3\sqrt{35}=0\)
Đúng 0
Bình luận (0)
Cho
M
1
;
1
;
0
và
P
:
2
x
-
y
+
2
z
2
0
. Viết phương trình mặt phẳng (Q) song song với (P) và khoảng cách M tới (Q) bằng 1.
Đọc tiếp
Cho M 1 ; 1 ; 0 và P : 2 x - y + 2 z = 2 = 0 . Viết phương trình mặt phẳng (Q) song song với (P) và khoảng cách M tới (Q) bằng 1.
