Ta có: M(x, y, z) ∈ (P)
⇔ d(M, ( P 1 )) = d(M, ( P 2 ))
⇔|2x + y + 2z + 1| = |2x + y + 2z + 5|
⇔ 2x + y + 2z + 1 = – (2x + y + 2z + 5)
⇔ 2x + y + 2z + 3 = 0
Từ đó suy ra phương trình của (P) là: 2x + y + 2z + 3 = 0.
Ta có: M(x, y, z) ∈ (P)
⇔ d(M, ( P 1 )) = d(M, ( P 2 ))
⇔|2x + y + 2z + 1| = |2x + y + 2z + 5|
⇔ 2x + y + 2z + 1 = – (2x + y + 2z + 5)
⇔ 2x + y + 2z + 3 = 0
Từ đó suy ra phương trình của (P) là: 2x + y + 2z + 3 = 0.
Trong không gian Oxyz, lập phương trình mặt phẳng (P) đi qua điểm A(2;-1;-2) và song song với mặt phẳng (Q): 2x - y + 2z = 0
A. 2x - y + 2z - 1 = 0
B. 2x - y + 2z + 9 = 0
C. 2x - y - 2z + 1 = 0
D. 2x - y + 2z + 1 = 0
Tính khoảng cách h giữa hai mặt phẳng song song: P : 2 x - y + 2 z - 1 = 0 và Q : 2 x - y + 2 z + 1 = 0 .
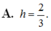
![]()
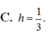
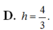
Phương trình mặt phẳng qua giao tuyến của hai mặt phẳng (P)x-3y+2z-1=0 và (Q)2x+y-3z+1=0 và song song với trục Ox là
Cho M 1 ; 1 ; 0 và P : 2 x - y + 2 z = 2 = 0 . Viết phương trình mặt phẳng (Q) song song với (P) và khoảng cách M tới (Q) bằng 1.
![]()
![]()
![]()
![]()
Cho điểm A (1; 2; 3) và hai mặt phẳng (P) :2x + 2y + z +1 = 0, (Q) : 2x - y + 2z - 1 = 0. Phương trình đường thẳng d đi qua A song song với cả (P) và (Q) là
![]()
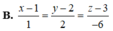
![]()
![]()
Trong không gian Oxyz, viết phương trình mặt phẳng (P) song song với mặt phẳng ( Q ) : x + 2 y – 2 z + 1 = 0 và tiếp xúc với mặt cầu ( S ) : x 2 + y 2 + z 2 + 2 x – 4 y – 2 z – 3 = 0
A. x + 2 y – 2 z + 6 = 0 ; x + 2 y – 2 z – 12 = 0
B. x + 2 y – 2 z + 8 = 0 ; x + 2 y – 2 z – 10 = 0
C. x + 2 y – 2 z + 10 = 0 ; x + 2 y – 2 z – 8 = 0 .
D. x + 2 y – 2 z + 12 = 0 ; x + 2 y – 2 z – 6 = 0
Trong không gian Oxyz, viết phương trình mặt phẳng (P) song song với mặt phẳng ( Q ) : x + 2 y - 2 z + 1 = 0 và tiếp xúc với mặt cầu ( S ) : x 2 + y 2 + z 2 + 2 x – 4 y – 2 z – 3 = 0
A. x + 2 y – 2 z + 12 = 0 v à x + 2 y – 2 z - 6 = 0
B. x + 2 y – 2 z – 12 = 0 v à x + 2 y – 2 z + 6 = 0
C. x + 2 y – 2 z + 10 = 0 v à x + 2 y – 2 z - 8 = 0
D. x + 2 y – 2 z – 10 = 0 v à x + 2 y – 2 z + 8 = 0
Trong không gian Oxyz, tập hợp các điểm M cách đều hai mặt phẳng (P): 2x + 3y + z - 1 = 0 và (Q): 3x + y + 2z - 3 = 0 là hai mặt phẳng có phương trình là:
A. x - 2y + z - 2 = 0 và 5x + 4y + 4z - 4 = 0
B. x - 2y + z - 2 = 0 và 5x + 4y + 3z - 4 = 0
C. x - 3y + z - 2 = 0 và 5x + 4y + 3z - 4 = 0
D. x + 2y + z - 2 = 0 và 5x + 4y + 3z - 4 = 0
Cho hai mặt phẳng:
( P 1 ): 2x + y + 2z + 1 = 0 và ( P 2 ): 4x – 2y – 4z + 7 = 0.
Lập phương trình mặt phẳng sao cho khoảng cách từ mỗi điểm của nó đến ( P 1 ) và ( P 2 ) là bằng nhau.