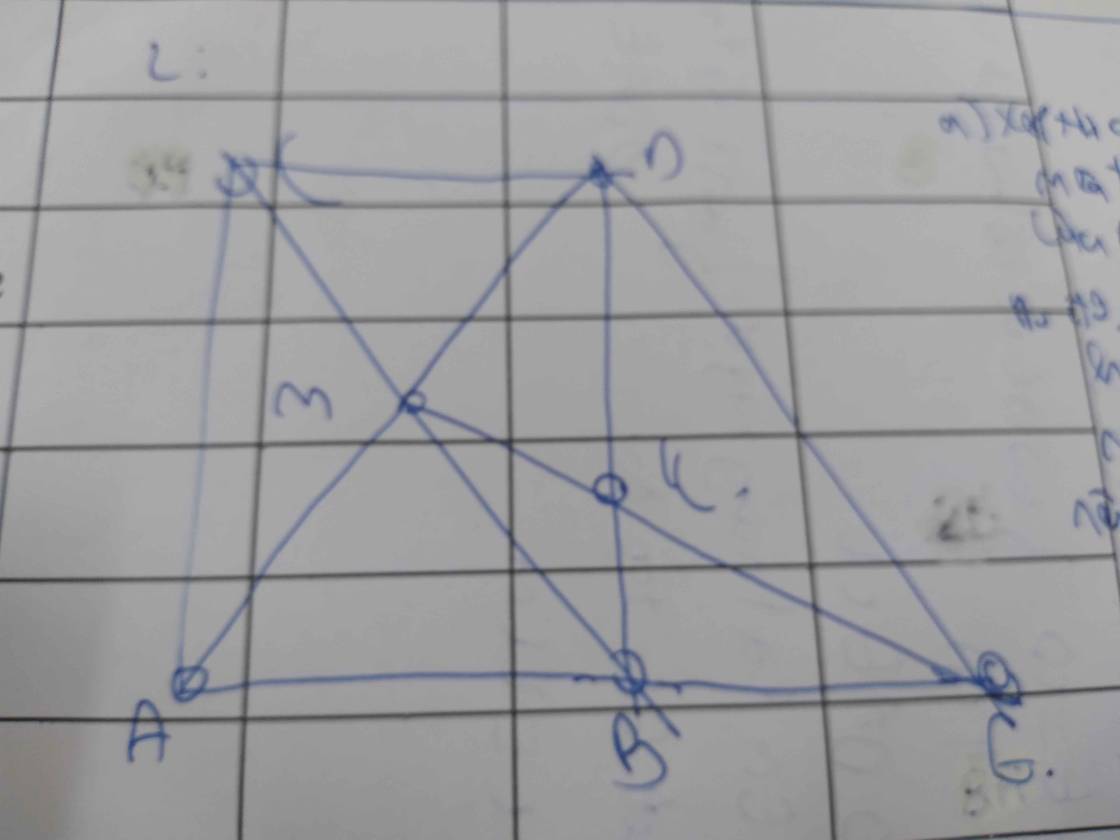
 Cho tam giác ABC vuông tại A, AH là đường cao, AM là đường trung tuyến .(H;HA) cắt tia AB tại D và tia AC tại E
Cho tam giác ABC vuông tại A, AH là đường cao, AM là đường trung tuyến .(H;HA) cắt tia AB tại D và tia AC tại E
a/ Chứng minh ba điểm D,H,E thẳng hàng
b/ Chứng minh MA vuông góc DE
c/ giả sử góc C bằng 30 độ ,AB = 4cm. tính diện tích tam giác HAC.

Những câu hỏi liên quan
Cho tam giác abc vuông tại a, đường cao ah, trung tuyến am. Từ h vẽ đường vuông góc với ac, đường thẳng này cắt am tại n. Chứng minh abhn là hình thang cân
làm tương tự

Bài làm

.....................
k mk nhé
Đúng 0
Bình luận (0)
hình như đề sai hay sao ấy. đã cho tg ABC vuông cân tại A. đg cao AH r còn có đg trung tuyến AM
Đúng 0
Bình luận (0)
AB vuông góc AC
HN vuông góc AC
=> AB//HN(từ vuông góc đến song song)
=> ABHN là hình thang
mà góc A = 90
=> ABHN là hthang vuông
ủa mà ABHN là hthang vuông mà bạn
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho tam giác ABC cân tại A đường cao ah gọi E,F lần lượt là chân đường vuông góc hạ từ H xuống AB,AC a) c/m EF=AH b) Kẻ trung tuyến AM của tam giác ABC C/m AM vuông góc EF
Cho tam giác ABC vuông tại A đường cao AH gọi E F lần lượt là hình chiếu của h trên AB AC m là đường trung tuyến của tam giác chứng minh AM vuông góc với EF
Gọi O là giao của EF và AH, K là giao AM và EF
Vì \(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\) nên AEHF là hcn
Do đó \(OE=OF=OH=OA\)
\(\Rightarrow\Delta AOF\) cân tại O \(\Rightarrow\widehat{AFO}=\widehat{FAO}\left(1\right)\)
Vì AM là trung tuyến ứng với cạnh huyền BC nên \(AM=BM=CM=\dfrac{1}{2}BC\)
\(\Rightarrow\Delta AMC\) cân tại M \(\Rightarrow\widehat{MCA}=\widehat{MAC}\left(2\right)\)
Vì tam giác AHC vuông tại H nên \(\widehat{MCA}+\widehat{FAO}=90^0\left(3\right)\)
Từ \(\left(1\right)\left(2\right)\left(3\right)\Rightarrow\widehat{MAC}+\widehat{AFO}=90^0\)
Mà \(\widehat{AFO}+\widehat{MAC}+\widehat{AKF}=180^0\Rightarrow\widehat{AKF}=90^0\)
Vậy AM vuông góc EF
Đúng 2
Bình luận (0)
cho tam giác abc vuông tại a. Đường cao AH. Gọi E,F lần lượt là chân đường vuông góc hạ từ H xuống AB và AC. Kẻ trung tuyến AM của tam giác ABC. Chứng minh rằng AM vuông góc với EF
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D và E theo thứ tự là chân đường vuông góc kẻ từ H đến AB, AC.
a) Chứng minh AH = DE
b) kẻ trung tuyến AM của tam giác ABC. Chứng minh góc HAB = góc MAC
c) AM vuông góc DE
a, Vì \(\widehat{AEH}=\widehat{ADH}=\widehat{DAE}=90^0\) nên AEHD là hcn
Do đó AH=DE
b, Vì \(\widehat{HAB}=\widehat{MCA}\) (cùng phụ \(\widehat{CAH}\))
Mà \(\widehat{MCA}=\widehat{MAC}\) (do \(AM=CM=\dfrac{1}{2}BC\) theo tc trung tuyến ứng ch)
Vậy \(\widehat{HAB}=\widehat{MAC}\)
c, Gọi O là giao AM và DE
Vì AEHD là hcn nên \(\widehat{HAB}=\widehat{ADE}\Rightarrow\widehat{MAC}=\widehat{ADE}\)
Mà \(\widehat{ADE}+\widehat{AED}=90^0\left(\Delta AED\perp A\right)\) nên \(\widehat{MAC}+\widehat{ADE}=90^0\)
Xét tam giác AOE có \(\widehat{AOE}=180^0-\left(\widehat{MAC}+\widehat{ADE}\right)=90^0\)
Vậy AM⊥DE tại O
Đúng 1
Bình luận (0)
bài 20 cho tam giác abc vuông ở a (ab < ac) , đường trung tuyến am, đường cao ah. qua h vẽ đường thẳng vuông góc với ac, cắt am tại n. chứng minh tứ giác abhn là hình thang cân.
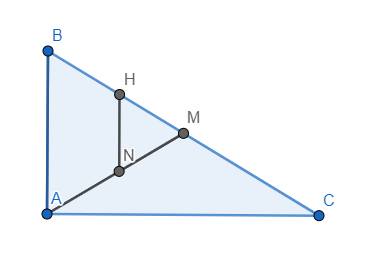
Ta có \(HN\perp AC\) và \(AB\perp AC\) nên AB//HN. Do đó tứ giác ABHN là hình thang (1)
Mặt khác, tam giác ABC vuông tại A có trung tuyến AM nên \(AM=\dfrac{1}{2}BC=BM\), suy ra tam giác MAB cân tại M hay \(\widehat{ABH}=\widehat{NAB}\) (2)
Từ (1) và (2), ta suy ra tứ giác ABHN là hình thang cân. (đpcm)
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH, đường trung tuyến AM. Gọi D, E theo thứ tự là chân đường vuông góc kể từ H đến AB, AC. Chứng minh rằng AM vuông góc với DE.
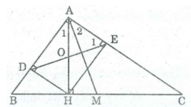
Xét tứ giác ADHE, ta có:
∠ A = 90 0 (gt)
∠ (ADH) = 90 0 (vì HD ⊥ AB)
∠ (AEH) = 90 0 (vì HE ⊥ AC)
Suy ra tứ giác ADHE là hình chữ nhật (vì có 3 góc vuông).
+ Xét ∆ ADH và ∆ EHD có :
DH chung
AD = EH ( vì ADHE là hình chữ nhật)
∠ (ADN) = ∠ (EHD) = 90 0
Suy ra: ∆ ADH = ∆ EHD (c.g.c)
⇒ ∠ A 1 = ∠ (HED)
Lại có: ∠ (HED) + ∠ E 1 = ∠ (HEA) = 90 0
Suy ra: ∠ E 1 + ∠ A 1 = 90 0
∠ A 1 = ∠ A 2 (chứng minh trên) ⇒ ∠ E 1 + ∠ A 2 = 90 0
Gọi I là giao điểm của AM và DE.
Trong ∆ AIE ta có: ∠ (AIE) = 180o – ( ∠ E 1 + ∠ A 2 ) = 180 0 - 90 0 = 90 0
Vậy AM ⊥ DE.
Đúng 0
Bình luận (0)
Phần Hình Học :Bài 1 : Cho Δ ABC vuông tại A có AH là đường cao, đường trung tuyến AM. Qua H kẻ HD // AC ( D ∈ AC). Đoạn DP cắt AH, AM lần lượt tại O và N. a, Chứng minh AH DP.b, ΔMAC là tam giác gì ?c, Chứng minh ΔAPN là tam giác vuông.Bài 2. Cho ΔABC vuông tại A có AB AC. Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD MA.a, Chứng minh ABCD là hình chữ nhật.b, Lấy điểm E sao cho B là trung điểm của AE. Chứng minh BEDC là hình bình hành.c, EM cắt BD tại K. Chứng mi...
Đọc tiếp
Phần Hình Học :
Bài 1 : Cho Δ ABC vuông tại A có AH là đường cao, đường trung tuyến AM. Qua H kẻ HD // AC ( D ∈ AC). Đoạn DP cắt AH, AM lần lượt tại O và N.
a, Chứng minh AH = DP.
b, ΔMAC là tam giác gì ?
c, Chứng minh ΔAPN là tam giác vuông.
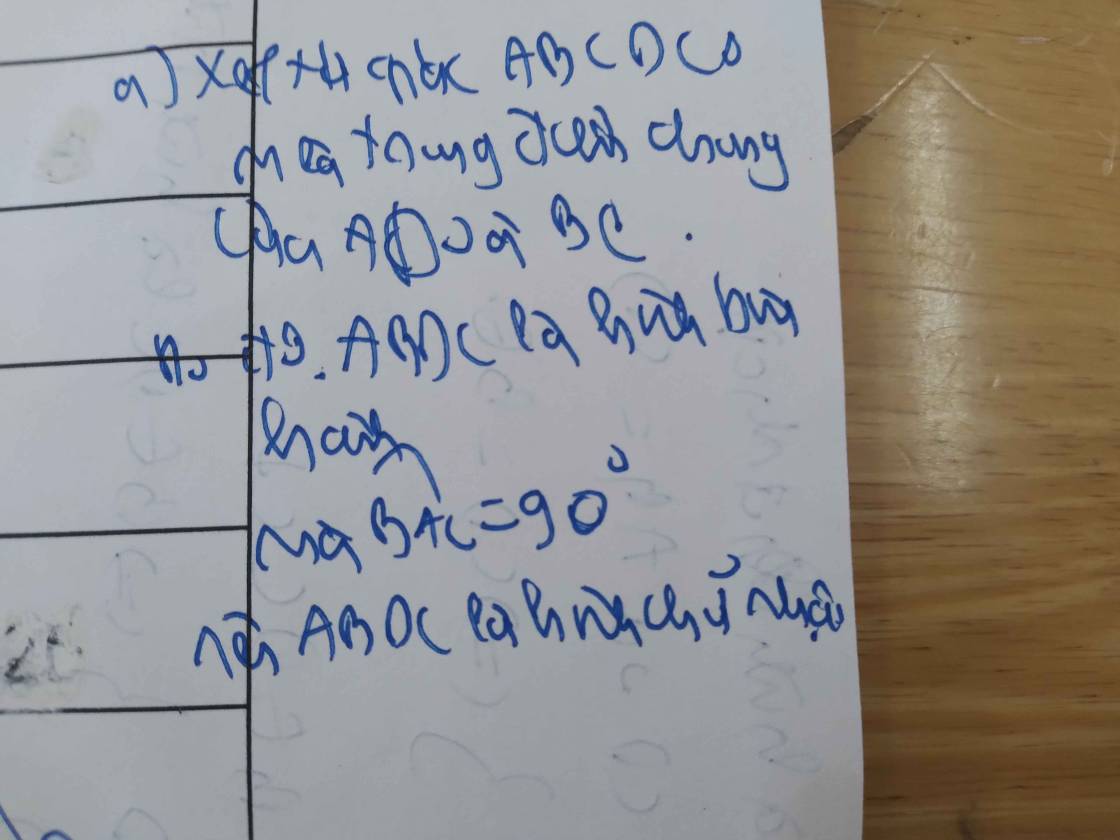
Bài 2. Cho ΔABC vuông tại A có AB < AC. Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a, Chứng minh ABCD là hình chữ nhật.
b, Lấy điểm E sao cho B là trung điểm của AE. Chứng minh BEDC là hình bình hành.
c, EM cắt BD tại K. Chứng minh EK = 2KM.
Cho tam giác ABC vuông tại A, AB = 5cm, AC = 12cm, đường cao AH. a) Tính BC, BH, AH. b) Gọi AM là đường trung tuyến của tam giác ABC, tính diện tích tam giác AHM
\(a,BC=\sqrt{AB^2+AC^2}=13\left(cm\right)\\ HTL:\left\{{}\begin{matrix}AH=\dfrac{AB\cdot AC}{BC}=\dfrac{60}{13}\left(cm\right)\\BH=\dfrac{AB^2}{BC}=\dfrac{25}{13}\left(cm\right)\end{matrix}\right.\\ b,AM=\dfrac{1}{2}BC=\dfrac{13}{2}\left(cm\right)\left(trung.tuyến.ứng.cạnh.huyền\right)\\ \Rightarrow HM=\sqrt{AM^2-AH^2}=\dfrac{119}{26}\left(cm\right)\\ \Rightarrow S_{AHM}=\dfrac{1}{2}AH\cdot HM=\dfrac{1}{2}\cdot\dfrac{60}{13}\cdot\dfrac{119}{26}=\dfrac{1785}{169}\left(cm^2\right)\)
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A biết AM = 6 cm , AC=8cm đường cao AH. Gọi DE lần lượt là chân đường vuông góc kẻ từ H đến AB và AC .
a, Tính diện tích tam giác ABC
b, Chứng minh : AM=DE
c,Kẻ trung tuyến AM của tam giác ABC. Chứng minh : AM vuông góc DE