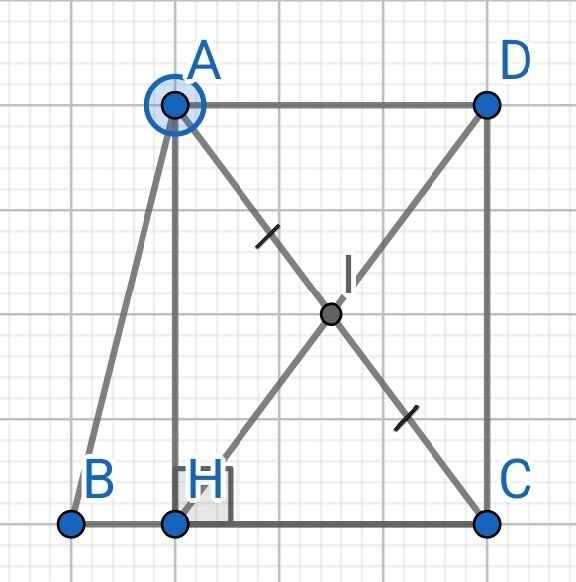
1. Cho tam giác ABC , đường cao AH . Gọi I là trung điểm của AC . Lấy D là điểm đối xứng với
H qua I . Chứng minh tứ giác AHCD là hình chữ nhật.
2. Cho tam giác ABC vuông tại A, đường cao AH . Gọi I , K theo thứ tự là trung điểm của AB ,
AC . Chứng minh:
a) IHK � 90� � ; b) Chu vi �IHK bằng nửa chu vi �ABC .
3. Tìm x trong hình vẽ bên, Biết AB �13 cm, BC �15 cm, AD �10
cm.
4. Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E , F , G , H theo thứ tự là
trung điểm của các cạnh AB , BC , CD, DA . Chứng minh tứ giác HEFG là hình chữ nhật.
5. Cho hình thang cân ABCD ( AB CD � , AB CD � ). Gọi M , N , P , Q lần lượt là trung điểm
các đoạn thẳng AD , BD , AC , BC .
a) Chứng minh bốn điểm M , N , P , Q thẳng hàng;
b) Chứng minh tứ giác ABPN là hình thang cân;
c) Tìm một hệ thức liên hệ giữa AB và CD để ABPN là hình chữ nhật.
6. Cho tam giác ABC có đường cao AI . Từ A kẻ tia Ax vuông góc với AC , từ B kẻ tia By
song song với AC . Gọi M là giao điểm của tia Ax và tia By . Nối M với trung điểm P của AB ,
đường MP cắt AC tại Q và BQ cắt AI tại H .
a) Tứ giác AMBQ là hình gì? b) Chứng minh tam giác PIQ cân.
7. Cho tam giác ABC . Gọi O là một điểm thuộc miền trong của tam giác. M ,
N , P , Q lần lượt là trung điểm của các đoạn thẳng OB , OC , AC , AB .
a) Chứng minh tứ giác MNPQ là hình bình hành;
b) Xác định vị trí của điểm O để tứ giác MNPQ là hình chữ nhật.