Cho \(\Delta ABC\) , kẻ AH\(\perp\)BC tại H
a. Chứng minh: AH<AB +\(\dfrac{AC}{2}\)
b. Kẻ BK\(\perp\)AC tại K, CI\(\perp\)AB tại I. Chứng minh AH+BK+CI nhỏ hơn chu vi của \(\Delta ABC\)

Những câu hỏi liên quan
Cho Δ ABC cân tại A(A<90độ).Kẻ AH⊥BC(H∈BC).Chứng minh:
a)ΔABH=ΔACH
b)Từ H kẻ HM⊥AB(M∈AB),HN⊥AC(N∈AC). Chứng minh :AM=AN
c)ΔBHM=ΔCHN
d)MN//BC
e)Biết BC=12cm,AH=8cm,MH=4,8cm. Tính AB,AN?
a) Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔABC cân tại A)
AH là cạnh chung
Do đó: ΔABH=ΔACH(cạnh huyền-cạnh góc vuông)
b) Ta có: ΔABH=ΔACH(cmt)
⇒\(\widehat{BAH}=\widehat{CAH}\)(hai góc tương ứng)
hay \(\widehat{MAH}=\widehat{NAH}\)
Xét ΔAMH vuông tại M và ΔANH vuông tại N có
AH là cạnh chung
\(\widehat{MAH}=\widehat{NAH}\)(cmt)
Do đó: ΔAMH=ΔANH(cạnh huyền-góc nhọn)
⇒AM=AN(hai cạnh tương ứng)
c) Ta có: ΔAHB=ΔAHC(cmt)
⇒HB=HC(hai cạnh tương ứng)
Xét ΔBMH và ΔCNH có
HB=HC(cmt)
\(\widehat{B}=\widehat{C}\)(hai góc ở đáy trong ΔABC cân tại A)
Do đó: ΔBMH=ΔCNH(cạnh huyền-góc nhọn)
d) Xét ΔAMN có AM=AN(cmt)
nên ΔAMN cân tại A(định nghĩa tam giác cân)
⇒\(\widehat{AMN}=\frac{180^0-\widehat{A}}{2}\)(số đo của một góc ở đáy trong ΔAMN cân tại A)(1)
Ta có: ΔABC cân tại A(gt)
⇒\(\widehat{ABC}=\frac{180^0-\widehat{A}}{2}\)(số đo của một góc ở đáy trong ΔABC cân tại A)(2)
Từ (1) và (2) suy ra \(\widehat{AMN}=\widehat{ABC}\)
mà \(\widehat{AMN}\) và \(\widehat{ABC}\) là hai góc ở vị trí đồng vị
nên MN//BC(dấu hiệu nhận biết hai đường thẳng song song)
e)
*Tính AB
Ta có: HB=HC(cmt)
mà HB+HC=BC(H nằm giữa B và C)
nên \(BH=CH=\frac{BC}{2}=\frac{12cm}{2}=6cm\)
Áp dụng định lí pytago vào ΔABH vuông tại H, ta được
\(AB^2=BH^2+AH^2\)
hay \(AB^2=6^2+8^2=100\)
⇒\(AB=\sqrt{100}=10cm\)
Vậy: AB=10cm
Đúng 0
Bình luận (0)
Cho DeltaABC vuông tại A,kẻ đường cao AH1)Chứng minh:DeltaABC đồng dạng DeltaHAC2)Cho AB6cm,AC8cm.Tính BC,AH3)Từ H kẻ HEperpAC.Chứng minh:^{HE^2}EA.EC4)Gọi I là trung điểm của AH,EI cắt AB tại F.Chứng minh:^{AH^2}FA.FB+EA.EC
Đọc tiếp
Cho \(\Delta\)ABC vuông tại A,kẻ đường cao AH
1)Chứng minh:\(\Delta\)ABC đồng dạng \(\Delta\)HAC
2)Cho AB=6cm,AC=8cm.Tính BC,AH
3)Từ H kẻ HE\(\perp\)AC.Chứng minh:\(^{HE^2}\)=EA.EC
4)Gọi I là trung điểm của AH,EI cắt AB tại F.Chứng minh:\(^{AH^2}\)=FA.FB+EA.EC
a/ Xét \(\Delta ABC\) và \(\Delta HAC\) có :
\(\left\{{}\begin{matrix}\widehat{C}chung\\\widehat{BAC}=\widehat{AHC}=90^0\end{matrix}\right.\)
\(\Leftrightarrow\Delta ABC\sim HAC\left(g-g\right)\)
b/ \(BC=\sqrt{AB^2+AC^2}=10cm\)
\(AH.BC=AB.AC\Leftrightarrow AH=\dfrac{AB.AC}{BC}=4,8cm\)
c/ \(\Delta HEA\sim\Delta CEH\left(g-g\right)\)
\(\Leftrightarrow\dfrac{HE}{CE}=\dfrac{EA}{HE}\Leftrightarrow HE^2=EA.EC\left(đpcm\right)\)
Đúng 2
Bình luận (0)

a) Xét ΔHAC và ΔABC có:
∠(ACH ) là góc chung
∠(BAC)= ∠(AHC) = 90o
⇒ ΔHAC ∼ ΔABC (g.g)
b) Xét ΔHAD và ΔBAH có:
∠(DAH ) là góc chung
∠(ADH) = ∠(AHB) = 90o
⇒ ΔHAD ∼ ΔBAH (g.g)

c) Tứ giác ADHE có 3 góc vuông ⇒ ADHE là hình chữ nhật.
⇒ ΔADH= ΔAEH ( c.c.c) ⇒ ∠(DHA)= ∠(DEA)
Mặt khác: ΔHAD ∼ ΔBAH ⇒ ∠(DHA)= ∠(BAH)
∠(DEA)= ∠(BAH)
Xét ΔEAD và ΔBAC có:
∠(DEA)= ∠(BAH)
∠(DAE ) là góc chung
ΔEAD ∼ ΔBAC (g.g)

d) ΔEAD ∼ ΔBAC

ΔABC vuông tại A, theo định lí Pytago:

Theo b, ta có:
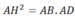


Đúng 1
Bình luận (0)
1) Xét ΔABC vuông tại A và ΔHAC vuông tại H có
\(\widehat{C}\) chung
Do đó: ΔABC\(\sim\)ΔHAC(g-g)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC cân tại A. Kẻ AH⊥BC , H∈BC
a) Chứng minh ΔABH = ΔACH
b) Kẻ HM⊥AB, M∈AB ; HN⊥AC, N∈AC . Chứng minh MB = NC
c) Gọi O là giao điểm AH và MN. Chứng minh MN//BC
https://i.imgur.com/pDLmg6N.jpg
Cho ΔABC cân tại A. Kẻ AH ⊥ BC ( H∈ BC)
a) Chứng mnh HB = HC
b) Kẻ HM⊥AB(M∈AB), HN⊥AC(N∈AC). Chứng minh ΔAMH = ΔANH
c) Tính diện tích ΔABC biết AB = 10cm, AH = 8cm
d) So sánh ABC và AMN, từ đó chứng minh MN song song với BC
a) Xét △ABC,ta có :△ABC cân tại A nên
AB=AC, ∠ABC = ∠ACB( t/c tam giác cân)
Vì AH⊥BC nên ∠AHB = ∠AHC
# Xét △AHB vs △AHC, ta có :
∠AHB=∠AHC(=90o)
AB=AC
∠ABC = ∠ACB
⇒△AHB = △AHC(ch-gn)
⇒HB=HC( 2 cạnh tương ứng )
b)Vì △AHB = △AHC(cmt) nên ∠HAB = ∠HAC(2 góc tương ứng)
Vì HM ⊥ AB nên ∠HMA =90o
Vì HN ⊥ AC nên ∠HMB =90o
#Xét △AHM vs △AHN, ta có:
∠AHM =∠AHN(=90o)
AH là cạnh chung
∠MAH=∠NAH(cmt)
⇒△AHM = △AHN (ch-gn)
c) Lúc nữa. ![]()
Cho Delta ABC cân tại A, lấy điểm M là trung điểm của cạnh BC. Trên tia đối của MA lấy điểm D sao cho MA MD
Chứng minh:
a) Delta AMB và Delta DMC
b) AC // BD
c) Kẻ AH perp BC, DK perp BC ( H, K in BC ) Chứng minh BK CH
Đọc tiếp
Cho \(\Delta ABC\) cân tại A, lấy điểm M là trung điểm của cạnh BC. Trên tia đối của MA lấy điểm D sao cho MA = MD
Chứng minh:
a) \(\Delta AMB\) và \(\Delta DMC\)
b) AC // BD
c) Kẻ AH \(\perp\) BC, DK \(\perp\) BC ( H, K \(\in\) BC ) Chứng minh BK = CH
Xét △AMD và △DMC
AB=AC(giả thuyết)
Cạnh AM là cạnh chung
BM= CM ( M là trung điểm của cạnh BC)
=> △AMD=△DMC
Sorry bạn nhé mk chỉ bt làm câu a thui ☹
Đúng 1
Bình luận (0)
Cho △ ABC cân tại A, ∠A=120 0 . Kẻ AH ⊥ BC (H ∈BC)
a) Chứng minh: HA = HC.
b) Kẻ HD ⊥ AB (D ϵAB), HE ⊥ BC (E ∈AC). Chứng minh HD = HE.
c) Chứng minh Δ HDE đều.
d) Chứng minh: DE // BC
 Ta có AB = AC
Ta có AB = AC
BD = CE
=> AB - BD = AC - CE
=> AD = AE
=>∆ADE cân tại A
=> ADE = (180° - BAC)/2 (t/c tam giác cân)
Mà ABC = (180° - BAC )/2 (∆ABC cân tại A)
=> ADE = ABC
Mà 2 góc này đồng vị
=> DE// BC
Đúng 0
Bình luận (0)
Cho DeltaABC vuông tại A, đường cao AH (HinBC)
a) Biết AB 12cm, BC 20cm. Tính AC, B, AH (góc làm tròn đến độ)
b) Kẻ HE perpAC (EinAC). Chứng minh: AE.ACAB2-HB2
c) Kẻ HF perpAB (FinAB). Chứng minh: AFAE.tanB
d) Chứng minh rằng dfrac{BF}{CE}dfrac{AB^3}{AC^3}
Đọc tiếp
Cho \(\Delta\)ABC vuông tại A, đường cao AH (H\(\in\)BC)
a) Biết AB = 12cm, BC = 20cm. Tính AC, B, AH (góc làm tròn đến độ)
b) Kẻ HE \(\perp\)AC (E\(\in\)AC). Chứng minh: AE.AC=AB2-HB2
c) Kẻ HF \(\perp\)AB (F\(\in\)AB). Chứng minh: AF=AE.tanB
d) Chứng minh rằng \(\dfrac{BF}{CE}\)=\(\dfrac{AB^3}{AC^3}\)
a) Để tính AC, ta sử dụng định lý Pythagoras trong tam giác vuông: AC^2 = AB^2 + BC^2. Với AB = 12cm và BC = 20cm, ta có: AC^2 = 12^2 + 20^2 = 144 + 400 = 544. Do đó, AC = √544 ≈ 23.32cm.
Để tính góc B, ta sử dụng công thức sin(B) = BC/AC. Với BC = 20cm và AC = 23.32cm, ta có: sin(B) = 20/23.32 ≈ 0.857. Từ đó, góc B ≈ arcsin(0.857) ≈ 58.62°.
Để tính AH, ta sử dụng công thức cos(B) = AH/AC. Với góc B ≈ 58.62° và AC = 23.32cm, ta có: cos(B) = AH/23.32. Từ đó, AH = 23.32 * cos(58.62°) ≈ 11.39cm.
b) Ta cần chứng minh AE.AC = AB^2 - HB^2. Vì ΔABC vuông tại A, ta có: AE = AB * sin(B) (theo định lý sin trong tam giác vuông) AC = AB * cos(B) (theo định lý cos trong tam giác vuông) HB = AB * sin(B) (theo định lý sin trong tam giác vuông)
Thay các giá trị vào biểu thức cần chứng minh: AE.AC = (AB * sin(B)) * (AB * cos(B)) = AB^2 * sin(B) * cos(B) = AB^2 * (sin(B) * cos(B)) = AB^2 * (sin^2(B) / sin(B)) = AB^2 * (1 - sin^2(B)) = AB^2 * (1 - (sin(B))^2) = AB^2 * (1 - (HB/AB)^2) = AB^2 - HB^2
Vậy, ta đã chứng minh AE.AC = AB^2 - HB^2.
c) Ta cần chứng minh AF = AE * tan(B). Vì ΔABC vuông tại A, ta có: AE = AB * sin(B) (theo định lý sin trong tam giác vuông) AF = AB * cos(B) (theo định lý cos trong tam giác vuông)
Thay các giá trị vào biểu thức cần chứng minh: AF = AB * cos(B) = AB * (cos(B) / sin(B)) * sin(B) = (AB * cos(B) / sin(B)) * sin(B) = AE * sin(B) = AE * tan(B)
Vậy, ta đã chứng minh AF = AE * tan(B).
d) Ta cần chứng minh tỉ lệ giữa các đường cao trong tam giác vuông ΔABC. CE/BF = AC/AB
Vì ΔABC vuông tại A, ta có: CE = AC * cos(B) (theo định lý cos trong tam giác vuông) BF = AB * cos(B) (theo định lý cos trong tam giác vuông)
Thay các giá trị vào biểu thức cần chứng minh: CE/BF = (AC * cos(B)) / (AB * cos(B)) = AC/AB
Vậy, ta đã chứng minh CE/BF = AC/AB.
Đúng 1
Bình luận (0)
Cho Delta ABC nhọn (AB AC). Trên nửa mặt phẳng bờ BC không chứa điểm A, vẽ tia cX song song với AB. Trên tia Cx, lấy điểm D sao cho CD AB.a) Chứng minh Delta ABCDelta DCBb) Chứng minh AC // BDc) Kẻ AHperp BC tại H, DCperp BK tại K. Chứng minh AH DK.d) Gọi I là trung điểm của BC. Chứng minh I là trung điểm của AD.
Đọc tiếp
Cho \(\Delta ABC\) nhọn (AB < AC). Trên nửa mặt phẳng bờ BC không chứa điểm A, vẽ tia cX song song với AB. Trên tia Cx, lấy điểm D sao cho CD = AB.
a) Chứng minh \(\Delta ABC=\Delta DCB\)
b) Chứng minh AC // BD\
c) Kẻ \(AH\perp BC\) tại H, \(DC\perp BK\) tại K. Chứng minh AH = DK.
d) Gọi I là trung điểm của BC. Chứng minh I là trung điểm của AD.
Cho ΔABC cân tại A (∠A<90 độ). Vẽ AH ⊥ BC tại H.
a. Chứng minh ΔAHB=ΔAHB.
b. Kẻ HM ⊥ AC tại M. Trên tia đối tia HM lấy điểm N sao cho HM=HN. Chứng minh BN // AC.
c. Kẻ HQ ⊥ AB tại Q. Chứng minh BC là đường trung trực của NQ.


b) Vì ΔAHC = ΔAHB ( câu a )
=> BH = HC ( Hai cạnh tương ứng )
Xét ΔBHN và ΔCHM, ta có:
BH = HC ( cmt )
Góc BHN = Góc CHM ( Hai góc đối đỉnh )
HN = HM ( gt )
=> ΔBHN = ΔCHM ( c-g-c )
=> Góc HMC = Góc BNH ( Hai góc tương ứng )
Mà góc HMC và góc BNH là hai góc so le trong
=> BN // AC
c)

























