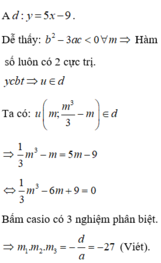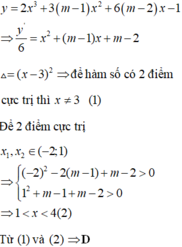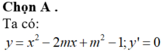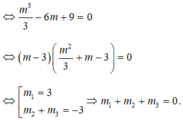Câu 9:Cho hai hàm số và
. Tập hợp các giá trị của
để
là

Những câu hỏi liên quan
Cho hàm số
f
x
−
5
x
2
+
14
x
−
9
.
Tập hợp các giá trị của x để
f
x
0
là A.
7
5
;...
Đọc tiếp
Cho hàm số f x = − 5 x 2 + 14 x − 9 . Tập hợp các giá trị của x để f ' x < 0 là
A. 7 5 ; 9 5 .
B. − ∞ ; 7 5 .
C. 1 ; 7 5 .
D. 7 5 ; + ∞ .
Đáp án A.
f ' x = − 10 x + 14 − 5 x 2 + 14 x − 9 với 1 < x < 9 5 . f ' x < 0 ⇔ − 10 x + 14 0 ⇔ x 14 10 = 7 5 .
Kết hợp với điều kiện thì x ∈ 7 5 ; 9 5 .
Đúng 0
Bình luận (0)
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị của hàm số
y
1
3
x
3
−
m
x
2
+
m
2
−
1
x
có hai điểm cực trị là A và B sao cho A,B nằm khác phía và cách đều đường thẳng
y
5
x...
Đọc tiếp
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị của hàm số y = 1 3 x 3 − m x 2 + m 2 − 1 x có hai điểm cực trị là A và B sao cho A,B nằm khác phía và cách đều đường thẳng y = 5 x − 9 . Tính tích các phần tử của S
A. 3
B. 0
C. 18
D. - 27
Gọi S là tập hợp tất cả các giá trị thực của tham số m để hàm số
y
1
3
x
3
-
m
x
2
+
(
m
2
-
1
)
x
có hai điểm cực trị A và B sao cho A, B nằm khác phía và cách đều đường thẳng d: y 5x- 9 . Tính tổng tất cả các phần tử của S. A. 0. B. 6. C. -6. D. 3.
Đọc tiếp
Gọi S là tập hợp tất cả các giá trị thực của tham số m để hàm số y = 1 3 x 3 - m x 2 + ( m 2 - 1 ) x có hai điểm cực trị A và B sao cho A, B nằm khác phía và cách đều đường thẳng d: y= 5x- 9 . Tính tổng tất cả các phần tử của S.
A. 0.
B. 6.
C. -6.
D. 3.
+ Ta có đạo hàm y’ = x2- 2mx+ (m2-1).
Phương trình y’ =0 có ∆ ' = m 2 - ( m 2 - 1 ) = 1 ⇒ x 1 = m - 1 x 2 = m + 1
+ Không mất tính tổng quát, giả sử A ( x 1 ; y 1 ) , B ( x 2 ; y 2 ) .
A, B nằm khác phía khi và chỉ khi x1. x2< 0 hay ( m-1) (m+ 1) < 0
Suy ra -1< m< 1
A, B cách đều đường thẳng y= 5x-9 suy ra trung điểm I của AB nằm trên đường thẳng đó.
Khi đó ta có:
I ( x 1 + x 2 2 ; y 1 + y 2 2 ) h a y I ( m ; 1 3 m 3 - m )
Ta có:
1 3 m 3 - m = 5 m - 9 ⇔ 1 3 m 3 - 6 m + 9 = 0 ⇔ m 1 = 3 1 3 m 2 + m - 3 = 0
Suy ra m 1 + m 2 + m 3 = 3 + - 1 1 3 = 0 .
Chọn A
Đúng 0
Bình luận (0)
Cho hàm số
y
2
x
3
+
3
m
−
1
x
2
+
6
m
−
2
x
−
1.
Gọi S là tập hợp tất cả các giá trị thực của m để hàm số có hai điểm cực trị đều thuộc (-2;1). Khi đó tập S là A.
S...
Đọc tiếp
Cho hàm số y = 2 x 3 + 3 m − 1 x 2 + 6 m − 2 x − 1. Gọi S là tập hợp tất cả các giá trị thực của m để hàm số có hai điểm cực trị đều thuộc (-2;1). Khi đó tập S là
A. S = 1 ; 4 .
B. S = ℝ \ 3 .
C. S = − ∞ ; 1 ∪ 4 ; + ∞ .
D. S = 1 ; 4 \ 3 .
Gọi là tập hợp tất cả các giá trị thực của tham số m để đồ thị của hàm số có hai điểm cực trị là A và B sao cho A, B nằm khác phía và cách đều đường thẳng . A 0 B. 6 C. -6 D. 3
Đọc tiếp
Gọi ![]() là tập hợp tất cả các giá trị thực của tham số m để đồ thị của hàm số
là tập hợp tất cả các giá trị thực của tham số m để đồ thị của hàm số ![]() có hai điểm cực trị là A và B sao cho A, B nằm khác phía và cách đều đường thẳng
có hai điểm cực trị là A và B sao cho A, B nằm khác phía và cách đều đường thẳng ![]() .
.
A 0
B. 6
C. -6
D. 3
(Đề tham khảo của Bộ) Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số
y
1
3
x
3
−
m
x
2
+
m
2
−
1
x
có hai điểm cực trị là A và B sao cho A,B nằm khác phía và cách đều đường thẳng
y...
Đọc tiếp
(Đề tham khảo của Bộ) Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số y = 1 3 x 3 − m x 2 + m 2 − 1 x có hai điểm cực trị là A và B sao cho A,B nằm khác phía và cách đều đường thẳng y = 5 x − 9. Tính tổng tất cả các phần tử của S.
A. -1.
B. 0.
C. 1.
D. 2.
Gọi S là tập hợp các giá trị thực của tham số m để hàm số
y
x
3
−
3
m
x
2
+
4
m
3
có hai điểm cực trị A và B sao cho tam giác OAB có diện tích bằng 4 (O là gốc tọa độ). Ta có tổng giá trị tất cả các phần tử của tập S bằng A. 1 B. 2 C. -1 D. 0
Đọc tiếp
Gọi S là tập hợp các giá trị thực của tham số m để hàm số y = x 3 − 3 m x 2 + 4 m 3 có hai điểm cực trị A và B sao cho tam giác OAB có diện tích bằng 4 (O là gốc tọa độ). Ta có tổng giá trị tất cả các phần tử của tập S bằng
A. 1
B. 2
C. -1
D. 0
Đáp án D
y = x 3 − 3 m x 2 + 4 m 3 ⇒ y ' = 3 x 2 − 6 m x . Ta có y ' = 0 ⇔ x = 0 x = 2 m
Để hàm số đã cho có 2 điểm cực trị thì m ≠ 0. Khi đó
y ' = 0 ⇔ x = 0 ⇒ y 0 = 4 m 3 ⇒ A 0 ; 4 m 3 ∈ O y x = 2 m ⇒ y 2 m = 0 ⇒ B 2 m ; 0 ∈ O x
Vậy tam giác OAB vuông tại O nên S Δ O A B = 1 2 O A . O B ⇔ 4 = 1 2 4 m 3 2 m
⇔ m 4 = 1 ⇔ m = − 1 m = 1 ⇒ S − 1 ; 1
Đúng 0
Bình luận (0)
Cho hàm số
y
2
x
3
-
3
m
2
-
m
+
1
x
2
+
6
m
2
-
6
m
x
, với m là tham số. Gọi S là t...
Đọc tiếp
Cho hàm số y = 2 x 3 - 3 m 2 - m + 1 x 2 + 6 m 2 - 6 m x , với m là tham số. Gọi S là tập hợp các giá trị của m để đồ thị hàm số đã cho có hai điểm cực trị, đồng thời đường thẳng đi qua hai điểm cực trị đó vuông góc với đường thẳng y = x + 2 . Số phần tử của tập hợp S là
A. 2
B. 3
C. 1
D. 4
Chọn đáp án D
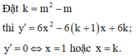
Đồ thị hàm số có hai điểm cực trị khi và chỉ khi k ≠ 1
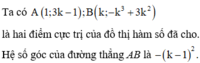
Đường thẳng AB vuông góc với đường thẳng y = x + 2 khi và chỉ khi

Đúng 0
Bình luận (0)
Cho hàm số
y
2
x
3
+
3
(
m
−
1
)
x
2
+
6
(
m
−
2
)
x
−
1
. Gọi S là tập hợp tất cả các giá trị thực của m để hàm số có hai điểm cực trị đều thuộc (-2;1). Khi đó tập S là A. S (1;4) B.
S
ℝ
3
C. ...
Đọc tiếp
Cho hàm số y = 2 x 3 + 3 ( m − 1 ) x 2 + 6 ( m − 2 ) x − 1 . Gọi S là tập hợp tất cả các giá trị thực của m để hàm số có hai điểm cực trị đều thuộc (-2;1). Khi đó tập S là
A. S = (1;4)
B. S = ℝ \ 3
C. S = − ∞ ; 1 ∪ 4 ; + ∞
D. S = ( 1 ; 4 ) \ 3
1) đạo hàm của hàm số \(\dfrac{2x^2+1}{x^2}\) là
2) cho hàm số \(f\left(x\right)=\sqrt{-5x^2+14x-9}\) tập hợp các giá trị của x để f'(x) = 0 là
1) \(y=\dfrac{2x^2+1}{x^2}\)
\(\Rightarrow y'=\dfrac{\left(4x+1\right)x^2-2x\left(2x^2+1\right)}{x^4}\)
\(\Leftrightarrow y'=\dfrac{4x^3+x^2-4x^3-2x}{x^4}\)
\(\Leftrightarrow y'=\dfrac{x^2-2x}{x^4}=\dfrac{x\left(x-2\right)}{x^4}=\dfrac{x-2}{x^3}\)
2) \(f\left(x\right)=\sqrt[]{-5x^2+14x-9}\)
\(\Rightarrow f'\left(x\right)=\dfrac{-10x+14}{2\sqrt[]{-5x^2+14x-9}}\)
\(\Leftrightarrow f'\left(x\right)=\dfrac{-2\left(5x-7\right)}{2\sqrt[]{-5x^2+14x-9}}\)
\(\Leftrightarrow f'\left(x\right)=\dfrac{-\left(5x-7\right)}{\sqrt[]{-5x^2+14x-9}}\)
Để \(f'\left(x\right)=0\)
\(f'\left(x\right)=\dfrac{-\left(5x-7\right)}{\sqrt[]{-5x^2+14x-9}}=0\)
\(\Leftrightarrow5x-7=0\)
\(\Leftrightarrow5x=7\)
\(\Leftrightarrow x=\dfrac{7}{5}\)
Vậy tập hợp giá trị để \(f'\left(x\right)=0\) là \(\left\{\dfrac{7}{5}\right\}\)
Đúng 1
Bình luận (0)