Giải phương trình :
a) a(ax +b) = b2(x-1)
b) a2x - ab = b2(x-1)
Những câu hỏi liên quan
Giải và biện luận phương trình sau:
1. ax2 - ab = b2(x - 1)
2. a(ax + b) = b2(x - 1)
2) Ta có: \(a\left(ax+b\right)=b^2\left(x-1\right)\)
\(\Leftrightarrow a^2x+ab=b^2x-b^2\)
\(\Leftrightarrow a^2x-b^2x=-b^2-ab\)
\(\Leftrightarrow x\left(a^2-b^2\right)=-b\left(b+a\right)\)
\(\Leftrightarrow x\left(b^2-a^2\right)=b\left(b+a\right)\)(1)
Nếu a=b thì (1) trở thành: \(0x=2b^2\)(vô nghiệm)
Nếu a=-b thì (1) trở thành: 0x=0(luôn đúng)
Nếu \(\left|a\right|\ne\left|b\right|\) thì \(x=\dfrac{b}{b-a}\)
Đúng 2
Bình luận (0)
Bài 1: Giải phương trình: a) b) (x+5)(x+2) – 3(4x-3) (5 – x) 2c) ( 3x – 1) 2 – 5( 2x + 1)2 + ( 6x – 3) ( 2x+ 1) ( x – 1)2Bài 2: Giải phương trình:a) b) Bài 3: Giải Phương trình với tham số a, ba) a ( ax+ b) b2 (x – 1)b) a2x – ab b2( x- 1) Bài 4: Giải phương trình mới tham số aa) b) c)
Đọc tiếp
Bài 1: Giải phương trình:
a)
b) (x+5)(x+2) – 3(4x-3) = (5 – x) 2
c) ( 3x – 1) 2 – 5( 2x + 1)2 + ( 6x – 3) ( 2x+ 1) = ( x – 1)2
Bài 2: Giải phương trình:
a)
b)
Bài 3: Giải Phương trình với tham số a, b
a) a ( ax+ b) = b2 (x – 1)
b) a2x – ab = b2( x- 1)
Bài 4: Giải phương trình mới tham số a
a)
b)
c)
Bài 1: Giải phương trình:
a)
b) (x+5)(x+2) – 3(4x-3) = (5 – x) 2
c) ( 3x – 1) 2 – 5( 2x + 1)2 + ( 6x – 3) ( 2x+ 1) = ( x – 1)2
Bài 2: Giải phương trình:
a)
b)
Bài 3: Giải Phương trình với tham số a, b
a) a ( ax+ b) = b2 (x – 1)
b) a2x – ab = b2( x- 1)
Bài 4: Giải phương trình mới tham số a
a)
b)
c)
\(\left(x+5\right)\left(x+2\right)-3\left(4x-3\right)=\left(5-x\right)2\)
\(\Leftrightarrow x^2+7x+10-12x+9=10-2x\)
\(\Leftrightarrow x^2-3x+9=0\)
Mà \(x^2-3x+9>0\)nên pt vô nghiệm
\(\left(x+5\right)\left(x+2\right)-3\left(4x-3\right)=\left(5-x\right)^2\)
\(\Leftrightarrow x^2-5x+19=x^2-10x+25\)
\(\Leftrightarrow x^2-5x+19-x^2=-10x+25\)
\(\Leftrightarrow-5x+19=-10x+25\)
\(\Leftrightarrow-5x+19-10x=25\)
\(\Leftrightarrow5x+19=25\)
\(\Leftrightarrow5x=25+19\)
\(\Leftrightarrow5x=6\)
\(\Leftrightarrow x=\frac{6}{5}\)
Xem thêm câu trả lời
Tìm đa thức A trong mỗi đẳng thức sau:a)
A
2
x
−
3
2
x
2
+
3
x
4
x
2
−
9
với x
≠
±...
Đọc tiếp
Tìm đa thức A trong mỗi đẳng thức sau:
a) A 2 x − 3 = 2 x 2 + 3 x 4 x 2 − 9 với x ≠ ± 3 2 ;
b) b 2 − 3 b 2 b 2 − 3 b − 9 = b 2 + 3 b A với b ≠ − 3 2 và b ≠ ± 3 .
Cách kết luận nghiệm phương trình
giả dụ 1 hệ phương trình nghiệm x,y cần đặt ẩn phụ là a và b. nếu a và b có 2 nghiệm, vd a= a1, a =a2, b=b1 và b=b2 thì khi giải x,y mình có ghép nghiệm : a1 và b1, a1 và b2, a2 và b1, a2 và b2 được không. và nếu kết luận nghiệm dư có bị trừ điểm không ?
Bất phương trình
2
log
4
3
x
+
1
-
log
2
3
-
x
≥
1
có tập nghiệm S [a;b). Tính
P
a
3
-
ab
+
b
2
.
A. P 4...
Đọc tiếp
Bất phương trình 2 log 4 3 x + 1 - log 2 3 - x ≥ 1 có tập nghiệm S = [a;b). Tính P = a 3 - ab + b 2 .
A. P = 43
B. P = 7
C. P = 23.
D. P =11
Có bao nhiêu cặp số nguyên (a;b) với
a
,
b
∈
0
;
10
để phương trình
x
2
+
a
x
+
b
2
+
a
x
2...
Đọc tiếp
Có bao nhiêu cặp số nguyên (a;b) với a , b ∈ 0 ; 10 để phương trình x 2 + a x + b 2 + a x 2 + a x + b + b = x có bốn nghiệm thực phân biệt.
A.33
B. 32
C. 34
D. 31
Cho hệ phương trình
(
a
+
b
)
x
+
(
a
-
b
)
y
...
Đọc tiếp
Cho hệ phương trình ( a + b ) x + ( a - b ) y = 2 ( 1 ) ( a 3 + b 3 ) x + a 3 - b 3 y = 2 ( a 2 + b 2 ) ( 2 )
Với a ≠ ± b , a b ≠ 0 hệ có nghiệm duy nhất bằng:
Tìm các giá trị của a (a0) để hệ phương trình
a
x
+
a
y
1
2
x
+
y...
Đọc tiếp
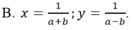
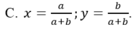
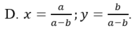
Tìm các giá trị của a (a>0) để hệ phương trình a x + a y = 1 2 x + y = b 2 - b + 1 có nghiệm ∀ b ∈ 0 ; 1
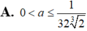
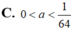
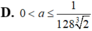
B1. Giải phương trình chứa dấu giá trị tuyệt đối
a. ||x| - 2| = 1
b. ||x| - 1| = x + 4
c. |3x + 2| + |1 - 2x| + |x| = 5
d. |2x - 8| + |x - 3| + |x - 2| = 9
B2. Giải bất phương trình
a. |2x + 1| < |x - 3|
b. |x - 2| - |x + 3| > 5 - 4x
Rút gọn biểu thức
a. 2x+2y/a2+2ab+b2 . ax-ay+bx-by/2x2-2y2
b. a+b-c/a2+2ab+b2-c2 . a2+2ab+b2+ac+bc/a2-b2
c.x3+1/x2+2x+1 . x2-1/2x2-2x+2
d. x8-1/x+1 . 1/ (x2+1) (x4+1)
e. x-y/xy+y2 - 3x+y/x2-xy . y-x/x+y
a2 c2... là em viết số mũ đó ạ. anh chị giúp em giải mấy bài này nha
\(a,\dfrac{2x+2y}{a^2+2ab+b^2}.\dfrac{ax-ay+bx-by}{2x^2-2y^2}\)
\(=\dfrac{2\left(x+y\right)}{\left(a+b\right)^2}.\dfrac{a\left(x-y\right)+b\left(x-y\right)}{2\left(x^2-y^2\right)}\)
\(=\dfrac{2\left(x+y\right)}{\left(a+b\right)^2}.\dfrac{\left(x-y\right)\left(a+b\right)}{2\left(x-y\right)\left(x+y\right)}\)
\(=\dfrac{1}{a+b}\)
\(b,\dfrac{a+b-c}{a^2+2ab+b^2-c^2}.\dfrac{a^2+2ab+b^2+ac+bc}{a^2-b^2}\)
\(=\dfrac{a+b-c}{\left(a+b\right)^2-c^2}.\dfrac{\left(a+b\right)^2+c\left(a+b\right)}{\left(a-b\right)\left(a+b\right)}\)
\(=\dfrac{a+b-c}{\left(a+b-c\right)\left(a+b+c\right)}.\dfrac{\left(a+b\right)\left(a+b+c\right)}{\left(a-b\right)\left(a+b\right)}\)
\(=\dfrac{1}{a-b}\)
\(c,\dfrac{x^3+1}{x^2+2x+1}.\dfrac{x^2-1}{2x^2-2x+2}\)
\(=\dfrac{\left(x+1\right)\left(x^2-x+1\right)}{\left(x+1\right)^2}.\dfrac{\left(x-1\right)\left(x+1\right)}{2\left(x^2-x+1\right)}\) \(=\dfrac{x-1}{2}\) \(d,\dfrac{x^8-1}{x+1}.\dfrac{1}{\left(x^2+1\right)\left(x^4+1\right)}\) \(=\dfrac{\left(x^4\right)^2-1}{x+1}.\dfrac{1}{\left(x^2+1\right)\left(x^4+1\right)}\) \(=\dfrac{\left(x^4-1\right)\left(x^4+1\right)}{x+1}.\dfrac{1}{\left(x^2+1\right)\left(x^4+1\right)}\) \(=\dfrac{\left(x^2+1\right)\left(x^2-1\right)}{x+1}.\dfrac{1}{x^2+1}\) \(=\dfrac{\left(x-1\right)\left(x+1\right)}{x+1}\) \(=x-1\) \(e,\dfrac{x-y}{xy+y^2}-\dfrac{3x+y}{x^2-xy}.\dfrac{y-x}{x+y}\) \(=\dfrac{x-y}{y\left(x+y\right)}-\dfrac{3x+y}{x\left(x-y\right)}.\dfrac{-\left(x-y\right)}{x+y}\) \(=\dfrac{x-y}{y\left(x+y\right)}-\dfrac{3x+y}{x}.\dfrac{-1}{x+y}\) \(=\dfrac{x-y}{y\left(x+y\right)}-\dfrac{-3x-y}{x\left(x+y\right)}\) \(=\dfrac{x\left(x-y\right)+y\left(3x+y\right)}{xy\left(x+y\right)}\) \(=\dfrac{x^2-xy+3xy+y^2}{xy\left(x+y\right)}\) \(=\dfrac{x^2+2xy+y^2}{xy\left(x+y\right)}\) \(=\dfrac{\left(x+y\right)^2}{xy\left(x+y\right)}=\dfrac{x+y}{xy}\)
Đúng 0
Bình luận (1)