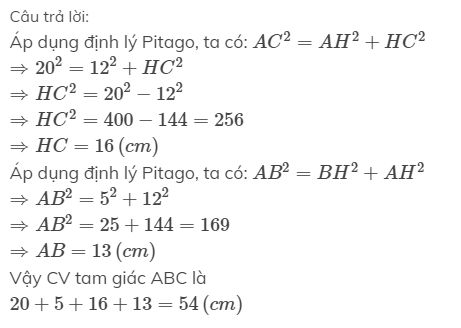Tam giác AHC vuông tại H nên :

AC2 = AH2 + HC2

202 = 122 + HC2

=> HC2 = 202 - 122

HC2 = 400 - 144 = 256 = 162

=> HC = 16 cm

Ta có : BC = HC + HB = 16 + 5 = 21 cm

Tam giác ABH vuông tại H nên :

AB2 = AH2 + HB2

AB2 = 122 + 52

AB2 = 144 + 25 = 169 = 132

=> AB = 13 cm

Vậy chu vi tam giác ABC là :

AB + AC + BC = 13 + 20 + 21 = 54 (cm)

chu vi là 54 cm

\(\Delta ABH\)vuông tại H \(\Rightarrow AH^2+BH^2=AB^2\)( định lý Pytago )

mà \(AH=12cm\), \(BH=5cm\)

\(\Rightarrow12^2+5^2=AB^2\)\(\Rightarrow AB^2=144+25\)

\(\Rightarrow AB^2=169\)\(\Rightarrow AB=13\)( cm )

\(\Delta AHC\)vuông tại H \(\Rightarrow AH^2+HC^2=AC^2\)( định lý Pytago )

\(\Rightarrow HC^2=AC^2-AH^2\)

mà \(AC=20cm\); \(AH=12cm\)

\(\Rightarrow HC^2=20^2-12^2\)\(\Rightarrow HC^2=400-144\)

\(\Rightarrow HC^2=256\)\(\Rightarrow HC=16\)( cm )

mà \(BC=HB+HC\)\(\Rightarrow BC=5+16=21\)( cm )

\(\Rightarrow P_{ABC}=AB+AC+BC=13+20+21=54\)( cm )

Vậy chu vi của \(\Delta ABC\)là 54 cm

\(AB^2=AH^2+BH^2\)

\(AB=12^2+5^2=169\)

\(AB=\sqrt{169}=13\left(cm\right)\)

▲AHC vuông tại H ta có:

HC\(^2\)=\(AC^2-AH^2\)=\(20^2-12^2\)=256

\(\)Chu vi ▲ABC là:

AB+BC+AC=AB+BH+HC+AC=\(13+5+16+20=54\left(cm\right)\)

Tham khảo: 

Tam giác AHC vuông tại H nên :

AC2 = AH2 + HC2

202 = 122 + HC2

=> HC2 = 202 - 122

HC2 = 400 - 144 = 256 = 162

=> HC = 16 cm

Ta có : BC = HC + HB = 16 + 5 = 21 cm

Tam giác ABH vuông tại H nên :

AB2 = AH2 + HB2

AB2 = 122 + 52

AB2 = 144 + 25 = 169 = 132

=> AB = 13 cm

Vậy chu vi tam giác ABC là :

AB + AC + BC = 13 + 20 + 21 = 54 (cm)

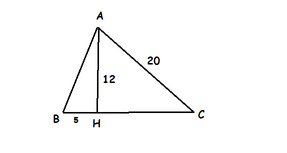
Ta có : \(\Delta ABH\) vuông tại H

Theo đl pytago ta có :   \(AH^2+BH^2=AB^2\)

-> \(AB=\sqrt{12^2+5^2}=13\left(cm\right)\)

 \(\Delta ACH\) vuông tại H

Theo đl pytago ta có :   \(AC^2-AH^2=CH^2\)

-. \(CH=\sqrt{20^2-12^2}=16\left(cm\right)\)

Chu vi \(\Delta ABC=AB+AC+BC=13+20+16+5=54\left(cm\right)\)

Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:

\(AB^2=AH^2+BH^2\)

\(\Leftrightarrow AB^2=12^2+16^2=400\)

hay AB=20(cm)

Áp dụng định lí Pytago vào ΔAHC vuông tại H, ta được:

\(AC^2=AH^2+HC^2\)

\(\Leftrightarrow HC^2=AC^2-AH^2=20^2-12^2=256\)

hay HC=16(cm)

Ta có: BH+HC=BC(H nằm giữa B và C)

nên BC=16+16=32(cm)

Chu vi của tam giác ABC là:

\(C_{ABC}=AB+BC+AC=20+32+20=72\left(cm\right)\)

Lời giải:

Áp dụng định lý Pitago cho tam giác $AHC$ vuông tại $H$:

$HC=\sqrt{AC^2-AH^2}=\sqrt{20^2-12^2}=16$ (cm)

Áp dụng định lý Pitago cho tam giác $AHB$ vuông tại $H$:

$AB=\sqrt{AH^2+BH^2}=\sqrt{12^2+16^2}=20$ (cm)

Chu vi tam giác $ABC$:

$AB+BC+AC=AB+BH+CH+AC=20+16+16+20=72$ (cm)

Hình vẽ:

Áp dụng PTG vào ΔAHB có: \(AH^2+BH^2=AB^2\Rightarrow AB=\sqrt{12^2+5^2}\Rightarrow AB=13\left(cm\right)\)

Áp dụng PTG vào ΔAHC có: \(AH^2+HC^2=AC^2\Rightarrow HC=\sqrt{20^2-12^2}\Rightarrow AH=16\left(cm\right)\)

Chu vi tam giác ABC là: \(AB+AC+HB+HC=13+20+5+16=54\left(cm\right)\)

Áp dụng định lý Pitago, ta có: \(AC^2=AH^2+HC^2\)

\(\Rightarrow20^2=12^2+HC^2\)

\(\Rightarrow HC^2=20^2-12^2\)

\(\Rightarrow HC^2=400-144=256\)

\(\Rightarrow HC=16\left(cm\right)\)

Áp dụng định lý Pitago, ta có: \(AB^2=BH^2+AH^2\)

\(\Rightarrow AB^2=5^2+12^2\)

\(\Rightarrow AB^2=25+144=169\)

\(\Rightarrow AB=13\left(cm\right)\)

Vậy CV tam giác ABC là

\(20+5+16+13=54\left(cm\right)\)

bạn vừa đăng rồi mà

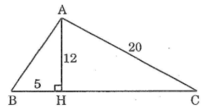
∆AHB có ∠(AHB) =90°

Theo định lý pitago, ta có:

AB2=AH2+HB2

= 122+52=169

Vậy AB = 13 cm

∆AHC có ∠(AHC) =90o

Theo định lý pitago, ta có:

AC2=AH2+HC2

HC2=AC2-AH2=202-122=400-144=256

Vậy HC = 16cm

Ta có: BC = BH + HC = 5 +16 = 21cm

Chu vi tam giác ABC là: AB + AC + BC = 13 + 20 + 21 = 54cm

Xét \(\Delta\)AHC vuông tại H:

=> AC² = HA² + HC²

HC² = AC² - HA²

HC² = 20² - 12² = 256

HC = \(\sqrt{256}\) = 16 (cm)

BC = BH + HC

BC = 5 + 16 = 21 (cm)

Xét \(\Delta\)AHB vuông tại H

=> AB² = HA² + HB²

AB² = 12² + 5²

AB² = 144 + 25 = 169

AB = \(\sqrt{169}\) = 13 (cm)

Chu vi của \(\Delta\)ABC là:

AC + CB + BA = 20 + 21 + 13

= 54 (cm)

Vậy chu vi của \(\Delta\)ABC là 54 cm.

Xét AHC vuông tại H:

=> AC2 = HA2 + HC2

HC2 = AC2 - HA2

HC2 = 202 - 122 = 256

HC = = 16 (cm)

BC = BH + HC

BC = 5 + 16 = 21 (cm)

Xét AHB vuông tại H

=> AB2 = HA2 + HB2

AB2 = 122 + 52

AB2 = 144 + 25 = 169

AB = = 13 (cm)

Chu vi của ABC là:

AC + CB + BA = 20 + 21 + 13

= 54 (cm)

Vậy chu vi của ABC là 54 cm.

a) Xét ΔAHB vuông tại H áp dụng định lý Py-ta-go ta có:

\(AB^2=AH^2+HB^2\)

\(\Rightarrow AB=\sqrt{AH^2+HB^2}\)

\(\Rightarrow AB=\sqrt{12^2+5^2}=13\left(cm\right)\) 

b) Xét ΔAHC vuông tại H áp dụng định lý Py-ta-go ta có:

\(AC^2=AH^2+HC^2\)

\(\Rightarrow HC=\sqrt{AC^2-AH^2}\)

\(\Rightarrow HC=\sqrt{20^2-12^2}=16\left(cm\right)\)

\(\Rightarrow BC=HB+HC=5+16=21\left(cm\right)\)

\(\Rightarrow C_{ABC}=BC+AB+AC=21+13+20=54\left(cm\right)\)