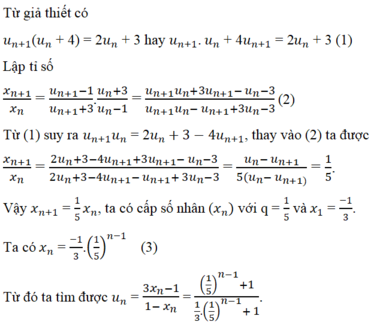Cho dãy số \(u_n=3^n-1\). Chứng minh dãy số này là cấp số nhân? Tìm u1 và q?

Những câu hỏi liên quan
Cho dãy số \({u_n}\)với \({u_n} = {2.5^n}\). Chứng minh rằng dãy số này là một cấp số nhân. Xác định số hạng đầu và công bội của nó.
Ta có: \(\frac{{{u_n}}}{{{u_{n - 1}}}} = \frac{{2 \times {5^n}}}{{2 \times {5^{n - 1}}}} = \frac{{2 \times {5^n}}}{{2 \times {5^{n}.5^{- 1}}}} = 5,\;\forall n \ge 2\).
Vậy dãy số \(\left( {{u_n}} \right)\) là một cấp số nhân với \({u_1} = 10\) và công bội \(q = 5\).
Đúng 0
Bình luận (0)
Cho dãy số \((u_n) \) thỏa mãn \(S_n=u_1+u_2+...+u_n=2^n-1\). Chứng minh rằng: dãy số \((u_n) \) là cấp số nhân.
Chứng minh , kiểm tra 1 dãy số có là cấp số cộng hay không ? xác định U1 , d
a , \(\left\{{}\begin{matrix}u_1\\u_n+1=u_n-n\end{matrix}\right.\)
b , \(\left\{{}\begin{matrix}u_1=a\\u_n+1=5\end{matrix}\right.\) tìm a để d số là cấp số cộng
Cho dãy số
(
u
n
)
:
u
1
0
u
n
+
1
...
Đọc tiếp
Cho dãy số ( u n ) : u 1 = 0 u n + 1 = 2 u n + 3 u n + 4 v ớ i n ≥ 1
a) Lập dãy số ( x n ) với x n = u n - 1 u n + 3 . Chứng minh dãy số là cấp số nhân.
b) Tìm công thức tính x n , u n theo n.
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = - 2n + 3\). Chứng minh rằng \(\left( {{u_n}} \right)\) là một cấp số cộng. Xác định số hạng đầu và công sai của cấp số cộng này.
Ta có: \({u_n} - {u_{n - 1}} = \left( { - 2n + 3} \right) - \left[ { - 2\left( {n - 1} \right) + 3} \right] = - 2,\;\forall n \ge 2\).
Vậy \({u_n} = - 2n + 3\) là một cấp số cộng với \({u_1} = 1\) và công sai \(d = - 2\).
Đúng 0
Bình luận (0)
Cho dãy số \(\left(u_n\right)\) với \(u_n=\left(-1\right)^n\left(-3\right)^{n+1}\)
a) Xét tính tăng, giảm của dãy số
b) Chứng minh rằng dãy số trên là cấp số nhân
c) Hỏi phải lấy tổng của bao nhiêu số hạng đầu của dãy số để được kết quả là : -265716
Cho dãy số left(u_nright):left{{}begin{matrix}u_10u_{n+1}dfrac{2u_n+3}{u_n+4};nge1end{matrix}right.
a) Lập dãy số left(x_nright) với x_ndfrac{u_n-1}{u_n+3}. Chứng minh dãy số left(x_nright) là cấp số nhân
b) Tìm công thức tính x_n,u_n theo n
Đọc tiếp
Cho dãy số \(\left(u_n\right):\left\{{}\begin{matrix}u_1=0\\u_{n+1}=\dfrac{2u_n+3}{u_n+4};n\ge1\end{matrix}\right.\)
a) Lập dãy số \(\left(x_n\right)\) với \(x_n=\dfrac{u_n-1}{u_n+3}\). Chứng minh dãy số \(\left(x_n\right)\) là cấp số nhân
b) Tìm công thức tính \(x_n,u_n\) theo \(n\)
Cho dãy số
u
1
1
3
u
n
+
1
...
Đọc tiếp
Cho dãy số u 1 = 1 3 u n + 1 = n + 1 u n 3 n v ớ i n ≥ 1
a) Viết năm số hạng đầu của dãy số.
b) Lập dãy số ( v n ) với v n = u n n . Chứng minh dãy số ( v n ) là cấp số nhân.
c) Tìm công thức tính ( u n ) theo n.
a) Năm số hạng đầu là 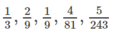
b) Lập tỉ số
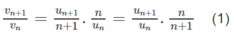
Theo công thứcđịnh nghĩa ta có 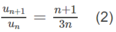
Từ (1) và (2) suy ra

Vậy, dãy số ( v n ) là cấp số nhân, có v 1 = 1 / 3 , q = 1 / 3
c) Để tính ( u n ) , ta viết tích của n - 1 tỉ số bằng 1/3
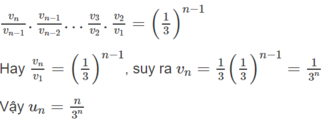
Đúng 0
Bình luận (0)
Cho dãy số \(\left(u_n\right)=\left(-3\right)^{2n-1}\)
a) Chứng minh dãy số \(\left(u_n\right)\) là cấp số nhân. Nêu nhận xét về tính tăng, giảm của dãy số
b) Lập công thức truy hồi của dãy số
c) Hỏi số -19683 là số hạng thứ mấy của dãy số ?
a) Có \(u_n=\left(-3\right)^{2n-1}=\left(-3\right)^2.\left(-3\right)^{2n-3}\)\(=9.2^{2\left(n-1\right)-1}=9.u_{n-1}\)
Vì vậy \(\left(u_n\right)\) là dãy số nhân với \(u_1=\left(-3\right)^{2.1-1}=-3\) và \(q=9\).
b) Công thức truy hồi của dãy số \(\left(u_n\right)\) là \(u_n=9u_{n-1}\).
c) Có \(u_n=\left(-3\right)^{2n-1}=-19683=\left(-3\right)^9\)\(\Leftrightarrow2n-1=9\)\(\Leftrightarrow n=5\).
Vậy số hạng thứ 5 bằng \(-19683\).
Đúng 0
Bình luận (0)
1) cho dãy số 1;3;9;27;.. là 1 cấp số nhân, viết 3 số tiếp theo của dãy số
2) cho cấp số nhân \(\left(u_n\right)\) có \(u_1=5\) và q = -2. Tính \(S_{11}\)
Bài 1: q=u2:u1=3:1=3
=> 3 số hạng tiếp theo: 81, 243, 729
Bài 2:
\(S_{11}=\dfrac{u_1.\left(q^{11}-1\right)}{q-1}=\dfrac{5.\left[\left(-2\right)^{11}-1\right]}{-2-1}\\ =\dfrac{5.\left(-2049\right)}{-3}=3415\)
Đúng 0
Bình luận (0)