a) Năm số hạng đầu là 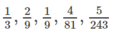
b) Lập tỉ số
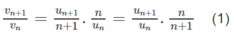
Theo công thứcđịnh nghĩa ta có 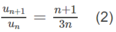
Từ (1) và (2) suy ra

Vậy, dãy số ( v n ) là cấp số nhân, có v 1 = 1 / 3 , q = 1 / 3
c) Để tính ( u n ) , ta viết tích của n - 1 tỉ số bằng 1/3
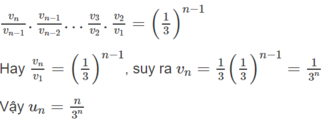
a) Năm số hạng đầu là 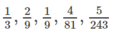
b) Lập tỉ số
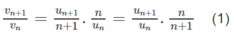
Theo công thứcđịnh nghĩa ta có 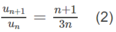
Từ (1) và (2) suy ra

Vậy, dãy số ( v n ) là cấp số nhân, có v 1 = 1 / 3 , q = 1 / 3
c) Để tính ( u n ) , ta viết tích của n - 1 tỉ số bằng 1/3
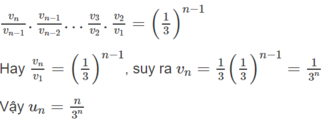
Cho dãy số u ( n ) xác định bởi u ( 1 ) = 1 ; u ( m + n ) = u ( m ) + u ( n ) + m n , ∀ m , n ∈ ℕ * . Tính u ( 2017 )
A. 2035153
B. 2035154
C. 2035155
D. 2035156
Cho dãy số (Un) xác định bởi U1=-3 và U(n+1)=Un+ n^2 -3n +4, mọi n thuộc N*. Số 1391 là số hạng thứ mấy của dãy ?
Cho dãy số u(n)=\(1/(2*4) +1/(5*7)+...+1/((3n-1)*(3n+1))\)
Tính Lim u(n).
Cho dãy số xác định bởi u1=1 , u n+1 = \(2un+\frac{n-1}{n^2+3n+2}\). khi đó u 2018 bằng
cho dãy số (un):\(\left\{{}\begin{matrix}u_1=\sqrt{3}+\sqrt{2}\\u_{n+1}=\left(\sqrt{3}-\sqrt{2}\right)u^2_n+\left(2\sqrt{6}-5\right)u_{n_{ }}+3\sqrt{3}-3\sqrt{2}\end{matrix}\right.\)
tìm lim(\(\Sigma^1_{i=1}\dfrac{1}{u_i+\sqrt{2}}\))
Cho dãy số (un) với un = \(\frac{1}{1.3}\)+ \(\frac{1}{3.5}\)+...+ \(\frac{1}{\left(2n-1\right)\left(2n+1\right)}\)Ta có lim un bằng bao nhiêu ?
cho dãy số \(\left\{{}\begin{matrix}u_1=2\\u_{n+1}=\dfrac{1}{2}\left(u^2_n+1\right)\end{matrix}\right.\) tìm lim\(\Sigma^n_{i=1}\dfrac{1}{u_i+1}\)
Cho dãy số được xác định bởi: U1=12
\(\frac{2\cdot U_{n+1}}{n^2+5n+6}=\frac{U_n+n^2-n-2}{n^2+n}\)
Tìm số hạng tổng quát của dãy số