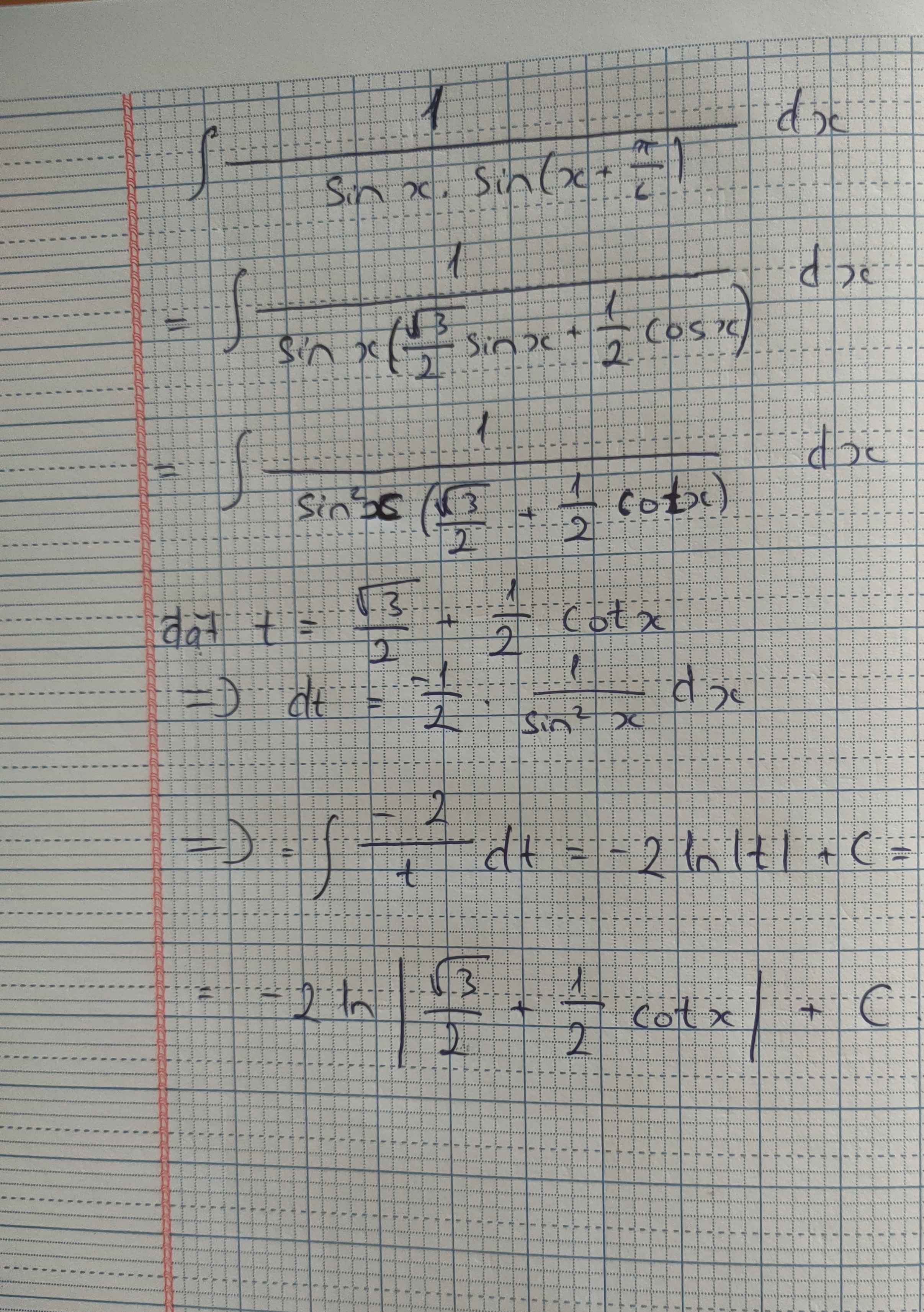tính nguyên hàm \(\int xcosxdx\) ọi người giúp với ạ

Những câu hỏi liên quan
Tìm nguyên hàm của hàm số f(x)=\(\int\dfrac{sinx+2cosx}{3cosx+sinx}dx\) bằng phương pháp đổi biến , giúp mình với ạ
\(\int tan\left(x\right)-ln^{15}\left(cos\left(x\right)\right)dx\)
\(\int\dfrac{x^4+x^2+1}{2x^3+5x^2-7}dx\)
tính nguyên hàm , ai giúp mình 2 bài này với hoặc 1 bài thôi cũng đc ạ , xin cảm ơn nhiều.
Tìm nguyên hàm của hàm số sau
∫
1
-
x
c
os
x
d
x
A.
1
+
x
cos
x
-
sin
x
+
C
B.
1
-
x
sin
x
-...
Đọc tiếp
Tìm nguyên hàm của hàm số sau ∫ 1 - x c os x d x
A. 1 + x cos x - sin x + C
B. 1 - x sin x - cos x + C
C. 1 - x cos x + sin x + C
D. 1 - x cos x - cos x + C
Chọn B
Đặt u = 1 - x d v = cos x d x ⇒ d u = - d x v = sin x
⇒ ∫ 1 - x cos x d x = 1 - x sin x + ∫ sin x d x = 1 - x sin x - cos x + C
Đúng 0
Bình luận (0)
Tìm nguyên hàm
I
∫
x
cos
x
d
x
.
A.
I
x
2
sin
x
2
+
C
.
B.
I
x
sin
x
+
cos
x
+
C
C.
I
x
sin...
Đọc tiếp
Tìm nguyên hàm I = ∫ x cos x d x .
A. I = x 2 sin x 2 + C .
B. I = x sin x + cos x + C
C. I = x sin x − c os x + C .
D. I = x 2 c o s x 2 + C .
Mọi người giải giúp em câu này với ạ Tính nguyên hàm |xdx/x^2 +3 (đặt u=x^2 +3) Em cảm ơn ạ
Ta có: \(\int\dfrac{xdx}{x^2+3}\)
Đặt \(u=x^2+3\left(u>0\right)\)
Có \(du=2xdx\)
\(\Rightarrow\int\dfrac{xdx}{x^2+3}=\)\(\int\dfrac{du}{2u}=\dfrac{1}{2}ln\left(u\right)=\dfrac{1}{2}ln\left(x^2+3\right)\)
Đúng 4
Bình luận (1)
ọi người ơi giúp mình với
-20<x<21
vậy x là gì vậy ạ
em ơi em chưa nói x thuộc gì nữa bọn anh học tới x thuộc R lậy còn nêu như x thuộc Z thì: \(x\in\left\{x=ℤ\backslash-20< x< 21\right\}\)
x={-19...20}
x=-19,-18,...,19,20
Xem thêm câu trả lời
Mấy bạn làm giúp mình câu nguyên hàm này với:
\(\int\dfrac{1}{sinx.sin\left(x+\dfrac{\pi}{6}\right)}dx\)
Tính nguyên hàm các hàm số sau:
1. \(I=\int\dfrac{cos^2x}{sin^8x}dx\)
2. \(I=\int\left(e^{sinx}+cosx\right)cosxdx\)
1.
\(I=\int\dfrac{cot^2x}{sin^6x}dx=\int\dfrac{cot^2x}{sin^4x}.\dfrac{1}{sin^2x}=\int cot^2x\left(1+cot^2x\right)^2.\dfrac{1}{sin^2x}dx\)
Đặt \(u=cotx\Rightarrow du=-\dfrac{1}{sin^2x}dx\)
\(I=-\int u^2\left(1+u^2\right)^2du=-\int\left(u^6+2u^4+u^2\right)du\)
\(=-\dfrac{1}{7}u^7+\dfrac{2}{5}u^5+\dfrac{1}{3}u^3+C\)
\(=-\dfrac{1}{7}cot^7x+\dfrac{2}{5}cot^5x+\dfrac{1}{3}cot^3x+C\)
Đúng 1
Bình luận (0)
2.
\(I=\int\left(e^{sinx}+cosx\right).cosxdx=\int e^{sinx}.cosxdx+\int cos^2xdx\)
\(=\int e^{sinx}.d\left(sinx\right)+\dfrac{1}{2}\int\left(1+cos2x\right)dx\)
\(=e^{sinx}+\dfrac{1}{2}x+\dfrac{1}{4}sin2x+C\)
Đúng 1
Bình luận (0)
Tính nguyên hàm của các hàm sau:
1. \(\int sin^2\)\(\dfrac{x}{2}\) dx
2. \(\int cos^23x\) dx
3. \(\int4cos^2\dfrac{x}{2}\) dx
\(\int sin^2\dfrac{x}{2}dx=\int\left(\dfrac{1}{2}-\dfrac{1}{2}cosx\right)dx=\dfrac{1}{2}x-\dfrac{1}{2}sinx+C\)
\(\int cos^23xdx=\int\left(\dfrac{1}{2}+\dfrac{1}{2}cos6x\right)dx=\dfrac{1}{2}x+\dfrac{1}{12}sin6x+C\)
\(\int4cos^2\dfrac{x}{2}dx=\int\left(2+2cosx\right)dx=2x+2sinx+C\)
Đúng 2
Bình luận (1)