Hãy nêu cách tính diện tích của hình cầu và hình trụ.
Cho một hình cầu và hình trụ ngoại tiếp nó (đường kính đáy và chiều cao của hình trụ bằng đường kính của hình cầu). Tính tỉ số giữa:
a, Diện tích mặt cầu và diện tích xung quanh của hình trụ
b, Thể tích hình cầu và thể tích hình trụ
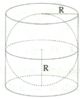
a, Tính được S S x q = 1
b, Tính được V h c V h t = 2 3
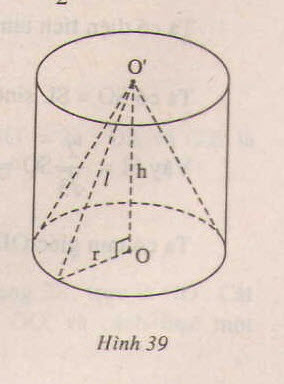
Cho hình trụ có bán kính đáy r, trục OO' = 2r và mặt cầu đường kính OO'
a) Hãy so sánh diện tích mặt cầu và diện tích xung quanh của hình trụ đó ?
b) Hãy so sánh thể tích khối trụ và thể tích khối cầu được tạo nên bởi hình trụ và mặt cầu đã cho ?
a, Diện tích của mặt cầu là: \(S_c=4\pi r^2\)
Diện tích xung quanh của mặt trụ là: \(S_t=2\pi rh=4\pi r^2\)
Vậy Sc = St
b, Thể tích của khối trụ là: \(V_t=\pi r^2h=2\pi r^2\)
Thể tích của khối cầu là: \(V_c=\dfrac{4}{3}\pi r^2\)
Vậy \(V_t=\dfrac{3}{2}V_c\)
1. Hãy phát biểu bằng lời:
a) Công thức tính diện tích xung quanh của hình trụ.
b) Công thức tính thể tích của hình trụ.
c) Công thức tính diện tích xung quanh của hình nón.
d) Công thức tính thể tích của hình nón.
e) Công thức tính diện tích của mặt cầu.
f) Công thức tính thể tích của hình cầu.
a) Diện tích xung quanh hình lăng trụ thì bằng chu vi đường tròn đáy nhân với chiều cao.
b) Thể tích hình trụ thì bằng tích của diện tích hình tròn đáy nhân với đường cao.
c) Diện tích xung quanh hình nón thì bằng 1/2 tích của chu vi đường tròn đáy với đường sinh.
d) Thể tích hình nón bằng 1/3 tích của diện tích hình tròn đáy với chiều cao.
e) Diện tích mặt cầu thì bằng 4 lần diện tích hình tròn lớn.
f) Thể tích hình cầu thì bằng 4/3 tích của diện tích hình tròn lớn với bán kính.
Cho hình trụ có bán kính r, trục OO' = 2r và mặt cầu đường kính OO'.
Hãy so sánh diện tích mặt cầu và diện tích xung quanh của hình trụ.
Do trục OO’= 2r nên chiều cao của khối trụ là h = 2r.
Mặt cầu có đường kính là OO’= 2r nên bán kính của mặt cầu là: R = r

Cho một hình trụ có bán kính đường tròn đáy là 3cm và chiều cao h = 4cm. Một hình cầu có diện tích bằng diện tích xung quang của hình trụ. Tính bán kính của hình cầu?
A. R = 3cm
B. R = 2cm
C. R = 3 cm
D. R = 6 cm
Một hình trụ có bán kính đáy r = 5cm và có khoảng cách giữa hai đáy bằng 7 cm.
a) Tính diện tích xung quanh của hình trụ và thể tích của khối trụ được tạo nên.
b) Cắt khối trụ bởi một mặt phẳng song song với trục và cách trục 3 cm. Hãy tính diện tích của thiết diện được tạo nên.
a) Theo đầu bài, hình trụ có chiều cao h = 7 cm và bán kính đáy r = 5 cm.
Vậy diện tích xung quanh bằng: Sxq= πrh = 35π (cm2)
Thể tích của khối trụ là:
V = πr2h = 175π (cm3)
b) Thiết diện là hình chữ nhật có một cạnh bằng chiều cao của hình trụ bằng 7 cm. Giả sử thiết diện là ABCD.
Ta có AD = 7 cm, OI = 3 cm.
Do tam giác OAI vuông tại A nên
AI2 = OA2 – OI2 = 25 – 9 = 16.
Vậy AI = 4 cm, AB = 8 cm.
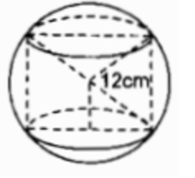
Một hình trụ được “đặt khít” vào bên trong một hình cầu bán kính r = 12cm như hình 112. Hãy tính: Diện tích xung quanh của hình trụ, biết chiều cao của hình trụ bằng đường kính đáy của nó.
Hãy quan sát lăng trụ đứng tam giác (Hình 1) và thực hiện các yêu cầu sau:
a) Tính tổng diện tích ba mặt bên của hình lăng trụ đứng
b) Gọi Cđáy là chu vi đáy và h là chiều cao của hình lăng trụ, tính Cđáy. h
c) So sánh kết quả của câu a và câu b
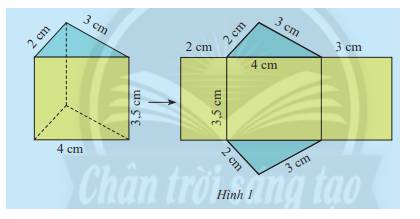
a) Tổng diện tích ba mặt bên của hình lăng trụ đứng là: S = 2 .3,5 +4. 3,5 + 3. 3,5 = 31,5 (cm2)
b) Chu vi đáy là: Cđáy = 2+3+4 = 9 (cm)
Cđáy. h = 9.3,5 = 31,5 (cm2)
c) Kết quả của câu a và câu b là như nhau
Một hình trụ có bán kính đáy \(r=5cm\) và có khoảng cách giữa hai đáy bằng 7cm.
a) Tính diện tích xung quanh của hình trụ và thể tích của khối trụ được tạo nên
b) Cắt khối trụ bởi một mặt phẳn song song với trục và cách trục 3cm. Hãy tính diện tích của thiết diện được tạo nên

a) Theo đầu bài, hình trụ có chiều cao h = 7 cm và bán kính đáy r = 5 cm.
Vậy diện tích xung quanh bằng: Sxq= πrh = 35π (cm2)
Thể tích của khối trụ là:
V = πr2h = 175π (cm3)
b) Thiết diện là hình chữ nhật có một cạnh bằng chiều cao của hình trụ bằng 7 cm. Giả sử thiết diện là ABCD.
Ta có AD = 7 cm, OI = 3 cm.
Do tam giác OAI vuông tại A nên
AI2 = OA2 – OI2 = 25 – 9 = 16.
Vậy AI = 4 cm, AB = 8 cm.

a) Theo đầu bài, hình trụ có chiều cao h = 7 cm và bán kính đáy r = 5 cm.
Vậy diện tích xung quanh bằng: Sxq= πrh = 35π (cm2)
Thể tích của khối trụ là:
V = πr2h = 175π (cm3)
b) Thiết diện là hình chữ nhật có một cạnh bằng chiều cao của hình trụ bằng 7 cm. Giả sử thiết diện là ABCD.
Ta có AD = 7 cm, OI = 3 cm.
Do tam giác OAI vuông tại A nên
AI2 = OA2 – OI2 = 25 – 9 = 16.
Vậy AI = 4 cm, AB = 8 cm.