Do trục OO’= 2r nên chiều cao của khối trụ là h = 2r.
Mặt cầu có đường kính là OO’= 2r nên bán kính của mặt cầu là: R = r

Do trục OO’= 2r nên chiều cao của khối trụ là h = 2r.
Mặt cầu có đường kính là OO’= 2r nên bán kính của mặt cầu là: R = r

Cho hình trụ có bán kính r, trục OO' = 2r và mặt cầu đường kính OO'.
Hãy so sánh thể tích khối trụ và thể tích khối cầu được tạo nên bởi hình trụ và mặt cầu đã cho.
Cho mặt cầu có bán kính R và cho một hình trụ có bán kính đáy R, chiều cao 2R. Tỉ số diện tích mặt cầu và diện tích xung quanh của hình trụ là
![]()
![]()
![]()
![]()
Hình trụ tròn xoay có bán kính đáy bằng r, có chiều cao bằng 2r và có trục là OO’. Thiết diện nói trên cắt mặt cầu đường kính OO’ theo thiết diện là một đường tròn. Tính bán kính của đường tròn đó.
Cho hình trụ có trục OO' và có bán kính đáy bằng 4. Một mặt phẳng song song với trục OO' và cách OO' một khoảng bằng 2 cắt hình trụ theo thiết diện là một hình vuông. Diện tích xung quanh của hình trụ đã cho bằng
![]()
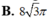
![]()
![]()
Cho hình trụ có trục OO' và có bán kính đáy bằng 4. Một mặt phẳng song song với trục OO' và cách OO' một khoảng bằng 2 cắt hình trụ theo thiết diện là một hình vuông. Diện tích xung quanh của hình trụ đã cho bằng
![]()
![]()
![]()
![]()
Cho hình trụ (T) có bán kính đáy a trục
OO' bằng 2a và mặt cầu (S) có tâm là
trung điểm của đoạn thẳng OO' và đi
qua điểm O. Tìm tỉ số giữa diện tích
mặt cầu (S) và diện tích toàn phần của
hình trụ (T).
![]()
![]()
![]()
![]()
Hình trụ tròn xoay có bán kính đáy bằng r, có chiều cao bằng 2r và có trục là OO’. Chứng minh rằng mặt cầu đường kính OO’ tiếp xúc với hai mặt đáy của hình trụ và tiếp xúc với tất cả các đường sinh của mặt trụ.
Hình trụ tròn xoay có bán kính đáy bằng r, có chiều cao bằng 2r và có trục là OO’. Cắt hình trụ bởi một mặt phẳng song song với trục OO’ và cách trục một khoảng bằng r/2. Tính diện tích thiết diện thu được.
Cho hình trụ có bán kính đáy r, gọi O và O' là tâm của hai đường tròn đáy với OO'=2r. Một mặt cầu tiếp xúc với hai đáy của hình trụ tại O và O'. Gọi V C và V T lần lượt là thể tích của khối cầu và khối trụ. Khi đó V C V T bằng
![]()
![]()
![]()
![]()