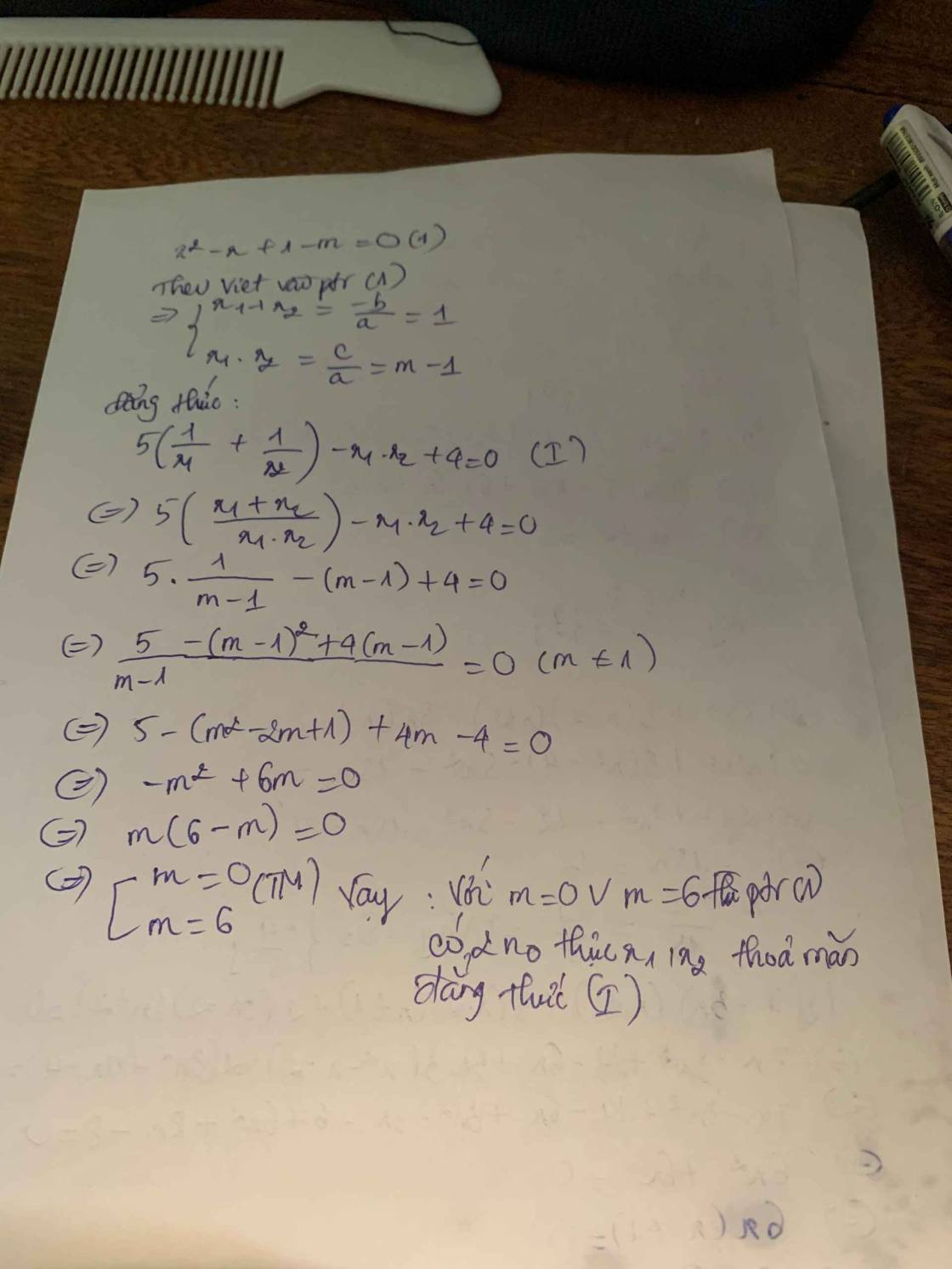a, ĐKXĐ: \(\hept{\begin{cases}x^3+1\ne0\\x^9+x^7-3x^2-3\ne0\\x^2+1\ne0\end{cases}}\)

b, \(Q=\left[\left(x^4-x+\frac{x-3}{x^3+1}\right).\frac{\left(x^3-2x^2+2x-1\right)\left(x+1\right)}{x^9+x^7-3x^2-3}+1-\frac{2\left(x+6\right)}{x^2+1}\right]\)

\(Q=\left[\frac{\left(x^3+1\right)\left(x^4-x\right)+x-3}{\left(x+1\right)\left(x^2-x+1\right)}.\frac{\left(x-1\right)\left(x+1\right)\left(x^2-x+1\right)}{\left(x^7-3\right)\left(x^2+1\right)}+1-\frac{2\left(x+6\right)}{x^2+1}\right]\)

\(Q=\left[\left(x^7-3\right).\frac{\left(x-1\right)}{\left(x^7-3\right)\left(x^2+1\right)}+1-\frac{2\left(x+6\right)}{x^2+1}\right]\)

\(Q=\frac{x-1+x^2+1-2x-12}{x^2+1}\)

\(Q=\frac{\left(x-4\right)\left(x+3\right)}{x^2+1}\)

giúp mik đc ko, mikk cần gấp

Ta có: \(\left\{{}\begin{matrix}\left(m-1\right)x-y=2\\mx+y=m\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left(m-1\right)x+mx=2+m\\mx+y=m\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\left(2m-1\right)=m+2\\mx+y=m\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{m+2}{2m-1}\\y=m-mx=m-m\cdot\dfrac{m+2}{2m-1}=m-\dfrac{m^2+2m}{2m-1}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{m+2}{2m-1}\\y=\dfrac{2m^2-m-m^2-2m}{2m-1}=\dfrac{m^2-3m}{2m-1}\end{matrix}\right.\)

Để x+y>0 thì \(\dfrac{m+2}{2m-1}+\dfrac{m^2-3m}{2m-1}>0\)

\(\Leftrightarrow\dfrac{m+2+m^2-3m}{2m-1}>0\)

\(\Leftrightarrow\dfrac{m^2-2m+2}{2m-1}>0\)

mà \(m^2-2m+2>0\forall m\)

nên 2m-1>0

\(\Leftrightarrow2m>1\)

hay \(m>\dfrac{1}{2}\)

Vậy: Để hệ phương trình có nghiệm duy nhất thỏa mãn x+y>0 thì \(m>\dfrac{1}{2}\)

\(\left\{{}\begin{matrix}\left(m-1\right)x-y=2\\mx+y=m\end{matrix}\right.\)

\(\Leftrightarrow\) \(\left\{{}\begin{matrix}\left(m-1\right)x-m+mx=2\\y=m-mx\end{matrix}\right.\)

\(\Leftrightarrow\) \(\left\{{}\begin{matrix}mx-x-m+mx=2\\y=m-mx\end{matrix}\right.\)

\(\Leftrightarrow\) \(\left\{{}\begin{matrix}2mx-x=2+m\\y=m-mx\end{matrix}\right.\)

\(\Leftrightarrow\) \(\left\{{}\begin{matrix}x\left(2m-1\right)=2+m\\y=m-mx\end{matrix}\right.\)

Hpt có nghiệm duy nhất \(\Leftrightarrow\) 2m - 1 \(\ne\) 0 \(\Leftrightarrow\) m \(\ne\) \(\dfrac{1}{2}\)

Khi đó: \(\left\{{}\begin{matrix}x=\dfrac{2+m}{2m-1}\\y=m-m.\dfrac{2+m}{2m-1}\end{matrix}\right.\)

\(\Leftrightarrow\) \(\left\{{}\begin{matrix}x=\dfrac{2+m}{2m-1}\\y=\dfrac{m^2-3m}{2m-1}\end{matrix}\right.\)

Vậy hpt có nghiệm duy nhất (x; y) = ...

Ta có: x + y > 0

\(\Leftrightarrow\) \(\dfrac{m^2-2m+2}{2m-1}>0\)

\(\Leftrightarrow\) \(\dfrac{\left(m-1\right)^2+1}{2m-1}\) > 0

\(\Leftrightarrow\) 2m - 1 > 0 (vì (m - 1)² + 1 > 0 với mọi m)

\(\Leftrightarrow\) 2m > 1

\(\Leftrightarrow\) m > \(\dfrac{1}{2}\)

Kết hợp với m \(\ne\) \(\dfrac{1}{2}\) ta có: m > \(\dfrac{1}{2}\) thì hpt có nghiệm duy nhất (x;y) thỏa mãn x + y > 0

Vậy m > \(\dfrac{1}{2}\)

Chúc bn học tốt! (Chắc đúng :D)

\(f\left(-1\right)=2\Rightarrow-a+b-c+d=2\\ f\left(0\right)=1\Rightarrow d=1\\ f\left(1\right)=7\Rightarrow a+b+c+d=7\\ f\left(\dfrac{1}{2}\right)=3\Rightarrow\dfrac{1}{8}a+\dfrac{1}{4}b+\dfrac{1}{2}c+d=3\)

\(d=1\Rightarrow-a+b-c=1;a+b+c=6\\ \Rightarrow2b=7\\ \Rightarrow b=\dfrac{7}{2}\\ \Rightarrow\dfrac{1}{8}a+\dfrac{7}{8}+\dfrac{1}{2}c=2\\ \Rightarrow\dfrac{1}{2}\left(\dfrac{1}{4}a+\dfrac{7}{4}+c\right)=2\\ \Rightarrow\dfrac{1}{4}a+\dfrac{7}{4}+c=4\\ \Rightarrow a+7+4c=16\\ \Rightarrow a+4c=9;a+c=6-\dfrac{7}{2}=\dfrac{5}{2}\\ \Rightarrow3c=\dfrac{13}{2}\Rightarrow c=\dfrac{13}{6}\\ \Rightarrow a=\dfrac{5}{2}-\dfrac{13}{6}=\dfrac{1}{3}\)

Vậy \(\left(a;b;c;d\right)=\left(\dfrac{1}{3};\dfrac{7}{2};\dfrac{13}{6};1\right)\)

help me: tìm n biết 2^n + 3^n = 5^n với n E N

\(x^2-x+1-m=0\)

Theo Vi - ét, ta có :

\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=1\\x_1x_2=\dfrac{c}{a}=1-m\end{matrix}\right.\)

Ta có :

\(5\left(\dfrac{1}{x_1}+\dfrac{1}{x_2}\right)-x_1x_2+4=0\)

\(\Leftrightarrow5\left(\dfrac{x_2+x_1}{x_1x_2}\right)-x_1x_2+4=0\)

\(\Leftrightarrow5\left(\dfrac{1}{1-m}\right)-\left(1-m\right)+4=0\)

\(\Leftrightarrow\dfrac{5}{1-m}-1+m+4=0\)

\(\Leftrightarrow\dfrac{5}{1-m}+m+3=0\)

\(\Leftrightarrow\dfrac{5+m\left(1-m\right)+3\left(1-m\right)}{1-m}=0\)

\(\Leftrightarrow5+m-m^2+3-3m=0\)

\(\Leftrightarrow-m^2-2m+8=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}m=2\\m=-4\end{matrix}\right.\)

Chọn B

Xét tử \(\left|4-x\right|+\left|x+2\right|\ge0\)

Xét mẫu \(\left|x+5\right|+\left|x-3\right|\ge0\)

Do đó \(\frac{\left|4-x\right|+\left|x+2\right|}{\left|x+5\right|+\left|x-3\right|}\ge0\)

Nhưng đề bài cho \(\frac{\left|4-x\right|+\left|x+2\right|}{\left|x+5\right|+\left|x-3\right|}=-\frac{1}{2}<0\) nên không có giá trị nào của x thỏa mãn.