kẽ đường cao AH,tam giác ABC cân tại A=>AH cũng là trung tuyến của BC=>BH=1/2BC=5cm 
xét tam giác AHB theo DL Pitago ta tính dc AH=12cm 
=>cosBAH=AH/AB=12/13 
=>cosBAC=2*12/13=24/13(vì AH là fân giác góc BAC)

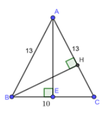
Vì tam giác ABC cân tại A nên AE là đường cao đồng thời là đường trung tuyến

=> E là trung điểm BC => EB = EC = 5

Xét ABE vuông tại E có:

Mặt khác:

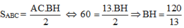
Xét ABH vuông tại H có:

Đáp án cần chọn là: A

a: XétΔADB và ΔADC có

AD chung

DB=DC

AB=AC

Do đó: ΔABD=ΔACD

b: ta có: ΔABC cân tại A

mà AD là trung tuyến

nên AD là đường cao

c: BD=BC/2=5cm

nên AD=12cm

a) Sửa đề: Cm AG vuông góc với BC

Ta có: \(AN=NB=\dfrac{AB}{2}\)(N là trung điểm của AB)

\(AM=MC=\dfrac{AC}{2}\)(M là trung điểm của AC)

mà AB=AC(ΔABC cân tại A)

nên AN=NB=AM=MC

Xét ΔNBC và ΔMCB có 

NB=MC(cmt)

\(\widehat{NBC}=\widehat{MCB}\)(hai góc ở đáy của ΔABC cân tại A)

BC chung

Do đó: ΔNBC=ΔMCB(c-g-c)

Suy ra: \(\widehat{NCB}=\widehat{MBC}\)(hai góc tương ứng)

hay \(\widehat{GBC}=\widehat{GCB}\)

Xét ΔGBC có \(\widehat{GBC}=\widehat{GCB}\)(cmt)

nên ΔGBC cân tại G(Định lí đảo của tam giác cân)

Suy ra: GB=GC(hai cạnh bên)

Ta có: AB=AC(ΔABC cân tại A)

nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)

Ta có: GB=GC(cmt)

nên G nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)

Từ (1) và (2) suy ra AG là đường trung trực của BC

hay AG\(\perp\)BC(đpcm)

Cho mk xin hình luôn nhé 

- Áp dụng định lý pi ta go vào tam giác ABC vuông tại A ta được :

\(AB^2+AC^2=BC^2\)

\(\Rightarrow AC^2+5^2=13^2\)

\(\Rightarrow AC=12\left(cm\right)\)

- Xét tam giác BHA và tam giác BAC có : \(\left\{{}\begin{matrix}\widehat{BHA}=\widehat{BAC}=90^o\\\widehat{B}\left(chung\right)\end{matrix}\right.\)

=> Hai tam giác trên đồng dạng .

=> \(\dfrac{BH}{AB}=\dfrac{AB}{BC}\)

=> \(BH=\dfrac{AB^2}{BC}=\dfrac{25}{13}\left(cm\right)\)

=> \(CH=BC-BH=\dfrac{144}{13}\left(cm\right)\)

- Áp dụng định lý pi ta go vào tam giác ABH vuông tại H ta được :

\(AH^2+BH^2=AB^2\)

\(\Rightarrow AH=\dfrac{60}{13}\left(cm\right)\)

Vậy ...

Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:

\(BC^2=AB^2+AC^2\)

\(\Leftrightarrow AC^2=BC^2-AB^2=13^2-5^2=144\)

hay AC=12(cm)

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:

\(AH\cdot BC=AB\cdot AC\)

\(\Leftrightarrow AH\cdot13=5\cdot12\)

\(\Leftrightarrow AH\cdot13=60\)

hay \(AH=\dfrac{60}{13}cm\)

Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:

\(AB^2=BH^2+AH^2\)

\(\Leftrightarrow BH^2=AB^2-AH^2=5^2-\left(\dfrac{60}{13}\right)^2=\dfrac{625}{169}\)

hay \(BH=\dfrac{25}{13}cm\)

Ta có: BH+CH=BC(H nằm giữa B và C)

\(\Leftrightarrow CH=BC-BH=13-\dfrac{25}{13}\)

hay \(CH=\dfrac{144}{13}cm\)

Vậy: AC=12cm; \(AH=\dfrac{60}{13}cm\); \(BH=\dfrac{25}{13}cm\); \(CH=\dfrac{144}{13}cm\)

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có

AB=AC

AH chung

Do đó: ΔAHB=ΔAHC

b: Ta có: ΔAHB=ΔAHC

nên HB=HC

=>HB=BC/2=6(cm)

Xét ΔAHB vuông tại H có 

\(AB^2=AH^2+BH^{ }\)

hay AH=8(cm)

c: Xét ΔABC có 

M là trung điểm của AC

N là trung điểm của AB

Do đó: MN là đường trung bình

=>MN//BC

d: Xét ΔNCB và ΔMBC có 

NB=MC

\(\widehat{NBC}=\widehat{MCB}\)

BC chung

Do đó: ΔNCB=ΔMBC

Suy ra: \(\widehat{GCB}=\widehat{GBC}\)

hay ΔGBC cân tại G

AC=12cm

  tự vẽ hình nhé                                                                                                       Gọi E là trung điểm của CD.

Xét tam giác BDC ta có:

M là trung điểm của BC ( gt )

E là trung điểm của CD (cách vẽ)

=> EM là đường trung trực của tam giác BDC.

=> EM // BD => EM // ID ( I thuộc BD )

Xét tam giác AME có:

I là trung điểm của AM (gt)

EM // ID (cmt)

=> D là trung điểm của AE

Xét tam giác AME có:

I là trung điểm của AM (gt)

D là trung điểm của AE (cmt)

=> ID là đường trung bình của tam giác AME.

Mà  ( ME là đường trung bình của tam giác BDC )

Nên 

Xét tam giác ABC vuông tại A ta có:

BC² = AB²+AC² ( Định lý Pitago thuận)

Thay: 

13² = 5² + AC²

169 = 25 + AC² => AC² = 169 - 25 = 144

=> AC² = 12²

=> AC = 12 (cm)

Ta có: AD = ED ( D là trung điểm của AE )

ED = EC ( E là trung điểm của DC)

=> AD = ED = EC

Mà AD + ED + EC = AC (gt)

Nên: AD + AD + AD = AC 

=> 3AD = AC

=> AD = AC/3

Mặt khác AC = 12 cm (cmt)

=> AD = 12/3 = 4 (cm)

Xét tam giác ABD vuông tại A ta có:

BD² = AB²+AD² ( định lý Pitago thuận)

BD² = 5²+4²

BD² = 25 + 20

BD² = 45

=> 

Thế (2) vào (1) ta được:

Ta có: 

BI + ID = BD ( I thuộc BD )

=> BI = BD - ID (4)

Thế (2), (3) vào (4) ta được:

Áp dụng định lí Py-ta-go vào tam giác ABC vuông tại A, ta có:

\(AB^2+AC^2=BC^2\\ AC^2=BC^2-AB^2\\ AC^2=13^2-5^2\\ AC^2=169-25\\ AC^2=144\\ AC=12\left(cm\right)\)

A/Vì AH vuông góc BC,mà TG ABC cân nên vừa là đường cao vừa là đường trung tuyến.

(Bạn có thể làm nhiều cách để giải thích rõ hơn chẳng hạn)

=>H là trung điểm của BC (t/c đường trung tuyến)

b/Ta có:BC=BH=CH=>CH=10:2=5(cm)

Mà ABC là TG cân =>AB=AC=13(cm)

Trong TG ACH:AH²=AC²-CH²(đ/ lí đảo Pytago)

AH²=13²-5²

=>AH²=12²

=>AH=12(cm)

Cho mình hỏi thêm đc ko :

c)Vẽ HE vuông góc AB, HF vuông góc AC (E thuộc AB, Fthuộc AC). Chứng minh HE = HF.

d)Chứng minh EF song song BC.