Gọi I a ; - a a > 0  thuộc đường thẳng y = - x

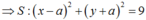
(S) tiếp xúc với các trục tọa độ 

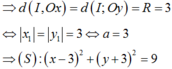
Chọn B.

Do tâm nằm trên đường thẳng ∆: x + 2y – 6 = 0 nên tâm là I(6 – 2y; y).

Đường tròn tiếp xúc với hai trục tọa độ nên:

6 − 2 y =    y    ⇔ 6 − 2 y = y 6 − 2 y =    − y ⇔ − 3 y = − 6 − y = − 6    ⇔ y = 2 y = 6

 Bán kính đường tròn là R = 2 hoặc R = 6

ĐÁP ÁN B

Do tâm (C) thuộc \(\Delta\) nên có dạng: \(I\left(-2a-3;a\right)\)

\(d\left(I;d\right)=R\Leftrightarrow\dfrac{\left|-2a-3-a+1\right|}{\sqrt{1^2+\left(-1\right)^2}}=\sqrt{2}\)

\(\Leftrightarrow\left|3a+2\right|=2\Rightarrow\left[{}\begin{matrix}a=0\\a=-\dfrac{4}{3}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}I\left(-3;0\right)\\I\left(-\dfrac{1}{3};-\dfrac{4}{3}\right)\end{matrix}\right.\)

Có 2 đường tròn thỏa mãn: \(\left[{}\begin{matrix}\left(x+3\right)^2+y^2=2\\\left(x+\dfrac{1}{3}\right)^2+\left(y+\dfrac{4}{3}\right)^2=2\end{matrix}\right.\)

a) Tâm của các đường tròn có bán kính 1cm tiếp xúc ngoài với đường tròn (O; 3cm) nằm trên đường tròn (O; 4cm).

b) Tâm của các đường tròn có bán kính 1cm tiếp xúc trong với đường tròn (O; 3cm) năm trên đường tròn (O; 2cm).

a) Đường tròn (C) tâm \(I(1;5)\), bán kính \(r = 4\) có phương trình là: \({\left( {x - 1} \right)^2} + {\left( {y - 5} \right)^2} = 16\)

b) \(MN = \sqrt {{{\left( {9 - 3} \right)}^2} + {{\left( {3 - ( - 1)} \right)}^2}}  = 2\sqrt {13} \), suy ra bán kính là \(\sqrt {13} \)

Tâm của đường tròn là trung điểm của MN: \(I(6;1)\)

Đường tròn (C) tâm \(I\left( {6;1} \right)\)và bán kính là \(\sqrt {13} \) có phương trình: \({\left( {x - 6} \right)^2} + {\left( {y - 1} \right)^2} = 13\)

c) Ta có bán kính của đường tròn \(r = d\left( {I,d} \right) = \frac{{\left| {5.2 - 12.1 + 11} \right|}}{{\sqrt {{5^2} + {{12}^2}} }} = \frac{9}{{13}}\)

Đường tròn (C) tâm \(I\left( {2;1} \right)\)và bán kính là \(\frac{9}{{13}}\) có phương trình: \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = \frac{{81}}{{169}}\)

d) Bán kính của đường tròn là \(r = AB = \sqrt {{{\left( {4 - 1} \right)}^2} + {{\left( {( - 5) - ( - 2)} \right)}^2}}  = 3\sqrt 2 \)

Đường tròn (C) tâm \(A(1; - 2)\)và bán kính là \(3\sqrt 2 \) có phương trình: \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 18\)

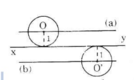
Gọi O là tâm của một đường tròn bất kì có bán kính bằng 1cm và tiếp xúc với đường thẳng xy.

Ta có: R = 1, và đường tròn tiếp xúc với đường thẳng xy nên ta có: d = R, suy ra d = 1.

=> Tâm O cách đường thẳng xy một khoảng cố định 1cm nên nằm trên các đường thẳng (a) và (b) song song với xy và cách xy một khoảng là 1cm.