∆ABC cân ở A có hai đường trung tuyến BM và CN cắt nhau ở I.
a) Chứng minh ∆AMN cân
b) Chứng minh ∆AMI = ∆ANI
c) Kéo dài AI cắt BC ở P. Biết AB = 10cm, BC = 16cm. Tính BP, AI, BI, CN
GIÚP MIK NHA ! THANK YOU VERY MUCH !
Cho \(\Delta ABC\) cân ở A có 2 đường trung tuyến BM và CN cắt nhau ở I
a/ C/m \(\Delta AMN\) cân
b/ C/m \(\Delta AMI=\Delta ANI\)
c/ Kéo dài AI cắt BC ở E. Biết AB=10cm, BC=16cm. Tính BE, AI, BI, CN
a: Xét ΔAMN có AM=AN
nên ΔAMN cân tại A
b: Xét ΔNBC va ΔMCB có
NB=MC
\(\widehat{NBC}=\widehat{MCB}\)
BC chung
Do đó; ΔNBC=ΔMCB
Suy ra: \(\widehat{ICB}=\widehat{IBC}\) và NC=MB
hay ΔIBC cân tại I
=>IB=IC
Ta có: IN+IC=CN
IM+IB=MB
mà CN=MB
và IB=IC
nên IN=IM
Xét ΔAMI và ΔANI có
AM=AN
IM=IN
AI chung
Do đó: ΔAMI=ΔANI
c: Ta có: AB=AC
IB=IC
Do đó: AI là đường trung trực của BC
=>E là trung điểm của BC
=>BE=BC/2=8(cm)
\(AE=\sqrt{10^2-8^2}=6\left(cm\right)\)
AI=2/3AE=4(cm)
Cho ΔABC cân tại A. Vẽ hai đường trung tuyến BM và CN cắt nhau tại I.
a) Chứng minh: ΔABM = ΔACN
b) Gọi H là giao điểm của AI và BC. Chứng minh: AH⊥BC
a: Xét ΔABM và ΔACN có
AB=AC
góc A chung
AM=AN
=>ΔABM=ΔACN
b: Xét ΔABC có
BM,CN là trung tuyến
BM cắt CN tại I
=>I là trọng tam
=>H là trung điểm của BC
ΔABC cân tại A
mà AH là trung tuyến
nên AH vuông góc BC
Cho tam giác ABC cân tại A có BM và CN là hai đường trung tuyến cắt nhau tại G
a) Chứng minh AM vuông góc BC
b) Cho AB = AC = 13cm, BC = 10cm, tính AG
c) Lấy I là trung điểm AB, chứng minh C, G, I thẳng hàng
a) Sửa đề: Cm AG vuông góc với BC
Ta có: \(AN=NB=\dfrac{AB}{2}\)(N là trung điểm của AB)
\(AM=MC=\dfrac{AC}{2}\)(M là trung điểm của AC)
mà AB=AC(ΔABC cân tại A)
nên AN=NB=AM=MC
Xét ΔNBC và ΔMCB có
NB=MC(cmt)
\(\widehat{NBC}=\widehat{MCB}\)(hai góc ở đáy của ΔABC cân tại A)
BC chung
Do đó: ΔNBC=ΔMCB(c-g-c)
Suy ra: \(\widehat{NCB}=\widehat{MBC}\)(hai góc tương ứng)
hay \(\widehat{GBC}=\widehat{GCB}\)
Xét ΔGBC có \(\widehat{GBC}=\widehat{GCB}\)(cmt)
nên ΔGBC cân tại G(Định lí đảo của tam giác cân)
Suy ra: GB=GC(hai cạnh bên)
Ta có: AB=AC(ΔABC cân tại A)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: GB=GC(cmt)
nên G nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AG là đường trung trực của BC
hay AG\(\perp\)BC(đpcm)
Ai giúp mình với
Cho tam giác ABC cân tại A và hai đường trung tuyến BM, CN cắt nhau tại K
a) Chứng minh tam giác BNC = tam giác CMB
b) Chứng minh tam giác BKC cân tại K
c) Chứng minh BC < 4.KM
a. Ta xét \(\Delta BCNvà\Delta CMB\)
có BC chung
góc B = góc C ( Hai góc ở đáy của tam giác cân)
BN = CM ( BN=\(\frac{1}{2}AB=\frac{1}{2}AC=CM\)
Suy ra tam giác BCN = tam giác CMB ( C-G-C)
b. Ta có tam giác BCN = tam giác CMB
suy ra góc BCN = góc CBM ( hai góc tương ứng)
tam giác BKC có góc KBC= góc KCB nên tam giác BKC cân tại K
c. Xét \(\Delta BKC\)
có BC< KB + KC ( BĐT tam giác) (1)
mà BK = 2.KM, CK = 2.KN mà BK= CK, KM =KN (2)
từ (1) và (2) suy ra BC < KB +KC =4.KM
Vậy BC < 4.KM
Cho tam giác ABC cân tại A có BM và CN là hai đường trung tuyến.
a) Chứng minh rằng BM = CN
b) Gọi I là giao điểm của BM và CN, đường thẳng AI cắt BC tại H. Chứng minh H là trung điểm của BC
Tham khảo:
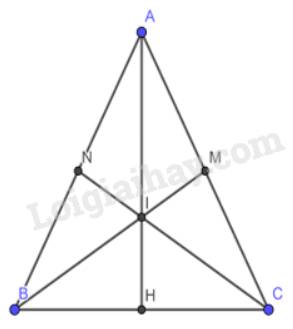
a) Vì tam giác ABC cân tại A theo giả thiết. BM và CN là 2 đường trung tuyến nên M, N là 2 trung điểm của AC, AB.
Vì AB = AC (tính chất tam giác cân)
\( \Rightarrow \dfrac{{AB}}{2} = \dfrac{{AC}}{2} = AN = AM\)
Xét tam giác AMB và tam giác ANC ta có :
AM = AN (cmt)
AB = AC
Góc A chung
\( \Rightarrow \Delta AMB =\Delta ANC\)
\( \Rightarrow BM = CN\) ( 2 cạnh tương ứng )
b) Vì BM và CN là các đường trung tuyến
Mà I là giao điểm của BM và CN
\( \Rightarrow \) I là trọng tâm của tam giác ABC
\( \Rightarrow \) AI là đường trung tuyến của tam giác ABC hay AH đường là trung tuyến của tam giác ABC
\( \Rightarrow \) H là trung điểm của BC
Cho tam giác ABC có 3 góc nhọn , hai đường cao BM và CN cắt nhau ở I . Tia AI cắt BC ở K . Chứng minh rằng:
a, tam giác AMN đồng dạng với tam giác ABC
b. tam giác AIB đòng dạng với tam giác MIK và AK.BM= AB.MK + AM.BK
a) Xét ΔAMB vuông tại M và ΔANC vuông tại N có
\(\widehat{BAM}\) chung
Do đó: ΔAMB\(\sim\)ΔANC(g-g)
Suy ra: \(\dfrac{AM}{AN}=\dfrac{AB}{AC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)
Xét ΔAMN và ΔABC có
\(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)(cmt)
\(\widehat{NAM}\) chung
Do đó: ΔAMN\(\sim\)ΔABC(c-g-c)
Cho tam giác ABC cân tại A và hai đường trung tuyến BM, CN cắt nhau tại K. Chứng minh : BC < 4KM
1) Cho tam giác ABC có BN, CN là 2 đường trung tuyến cắt nhau tại G. Kéo dài BM lấy ME= MG. Kéo dài NC lấy NF = NG. Chứng minh:
a) EF= BC.
b) đường thẳng AG đi qua trung điểm BC
2) Viết định nghĩa ? các đấu hiệu nhận biết tam giác cân
