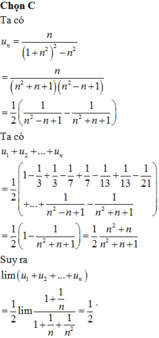cm n4-n2=n2(n+1)(n-1)
Những câu hỏi liên quan
Tìm giá trị nguyên của n để thương trong phép chia đa thức n4-3n3+n2-3n+1 cho đa thức n2+1 có giá trị nguyên.
Để chia \(n^4-3n^3+n^2-3n+1\) cho \(n^2+1\) có giá trị nguyên
⇔ \(n^4-3n^3+n^2-3n+1\) \(⋮n^2+1\)
⇔ \(1⋮n^2+1\)
\(\Leftrightarrow n^2+1\inƯ\left(1\right)=\left\{1;-1\right\}\)
| n2 + 1 | 1 | -1 |
|
n |
0 | ( loại ) |
Đúng 0
Bình luận (2)
3 tháng 8 2021 lúc 7:49
CMR:
n8-n6-n4+n2⋮1152 (n lẻ)
\(1152=32.36\)
Đặt \(A=n^8-n^6-n^4+n^2=n^6\left(n^2-1\right)-n^2\left(n^2-1\right)\)
\(=n^2\left(n^2-1\right)\left(n^4-1\right)=n^2\left(n^2-1\right)\left(n^2-1\right)\left(n^2+1\right)\)
\(=\left[n\left(n-1\right)\left(n+1\right)\right]^2\left(n^2+1\right)\)
Do \(n\) lẻ \(\Rightarrow n=2k+1\)
\(\Rightarrow A=\left[\left(2k+1\right)\left(2k+1-1\right)\left(2k+1+1\right)\right]^2\left[\left(2k+1\right)^2+1\right]\)
\(=32\left[k\left(k+1\right)\left(2k+1\right)\right]^2.\left(2k^2+2k+1\right)\)
Do \(k\) và k+1 là 2 số tự nhiên liên tiếp \(\Rightarrow k\left(k+1\right)⋮2\) (1)
Nếu k chia hết cho 3 \(\Rightarrow k\left(k+1\right)\left(2k+1\right)⋮3\)
Nếu k chia 3 dư 1 \(\Rightarrow2k+1⋮3\Rightarrow k\left(k+1\right)\left(2k+1\right)⋮3\)
Nếu k chia 3 dư 2 \(\Rightarrow k+1⋮3\Rightarrow k\left(k+1\right)\left(2k+1\right)⋮3\)
\(\Rightarrow k\left(k+1\right)\left(2k+1\right)\) luôn chia hết cho 3 (2)
(1);(2) \(\Rightarrow k\left(k+1\right)\left(2k+1\right)⋮6\Rightarrow\left[k\left(k+1\right)\left(2k+1\right)\right]^2⋮36\)
\(\Rightarrow32\left[k\left(k+1\right)\left(2k+1\right)\right]^2⋮\left(32.36\right)\Rightarrow A⋮1152\)
Đúng 1
Bình luận (0)
ảnh đại diện trên google kìa
c/m : n8 - n6 -n4 + n2 chia hết cho 1152 với mọi n lẻ và n ϵ N
Đặt: \(A=n^8-n^6-n^4+n^2\)
\(A=\left(n^8-n^6\right)-\left(n^4-n^2\right)\)
\(A=n^6\left(n^2-1\right)-n^2\left(n^2-1\right)\)
\(A=\left(n^2-1\right)\left(n^6-n^2\right)\)
\(A=\left(n-1\right)\left(n+1\right)n^2\left(n^4-1\right)\)
\(A=n^2\left(n-1\right)\left(n+1\right)\left[\left(n^2\right)^2-1\right]\)
\(A=n^2\left(n-1\right)\left(n+1\right)\left(n^2-1\right)\left(n^2+1\right)\)
\(A=n^2\left(n-1\right)\left(n+1\right)\left(n-1\right)\left(n+1\right)\left(n^2+1\right)\)
\(A=n\left(n-1\right)\left(n+1\right)n\left(n-1\right)\left(n+1\right)\left(n^2+1\right)\)
Ta có: \(n\left(n-1\right)\left(n+1\right)\) là tích của 3 số tự nhiên liên tiếp nên sẽ chia hết cho 3
Còn: \(\left[n\left(n-1\right)\left(n+1\right)\right]\left[n\left(n-1\right)\left(n+1\right)\right]\) sẽ chia hết cho \(3\times3=9\)
Do n sẽ là số lẻ nên \(\left(n-1\right);\left(n+1\right)\) sẽ luôn luôn là số chẵn
Mà: \(\left(n-1\right)\left(n+1\right)\) sẽ chia hết cho 8 vì tích của hai số chẵn liên liếp sẽ chia hết cho 8
Còn \(\left(n+1\right)\left(n-1\right)\left(n+1\right)\left(n-1\right)\left(n^2+1\right)\) sẽ chia hết cho \(8\cdot8\cdot2=128\)
Ta có:
\(\text{Ư}\text{C}LN\left(9;128\right)=1\)
Nên: A ⋮ \(9\cdot128=1152\left(dpcm\right)\)
Đúng 2
Bình luận (0)
tìm 9 số dườn khác nhau n1,n2,n3,n4,n5,n6,n7,n8,n9 thoả mãn
1/n1 + 1/n2 + 1/n3 + 1/n4 + 1/n5 + 1/n6 + 1/n7 + 1/n8 + 1/n9 = 1
Chứng minh với mọi số nguyên n thì A = n 4 - 2 n 3 - n 2 + 2n chia hết cho 24.
A = n 4 – 2 n 3 – n 2 +2n = (n – 2)(n – 1)n(n + 1) là tích của 4 số nguyên liên tiếp do đó A ⋮ 24 .
Đúng 0
Bình luận (0)
Cho dãy số
u
n
như sau :
u
n
:
n
1
+
n
2
+
n
4
,...
Đọc tiếp
Cho dãy số u n như sau : u n : n 1 + n 2 + n 4 , ∀ n = 1 , 2 , . . . Tính giới hạn l i m n → + ∞ u 1 + u 2 + . . . + u n
A. 1 4
B. 1
C. 1 2
D. 1 3
Đáp án C
Ta có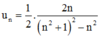 
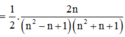
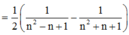
Đặt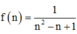 
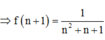suy ra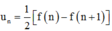 
Khi đó l i m u 1 + u 2 + . . . + u n
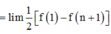
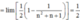
Đúng 0
Bình luận (0)
Cho dãy số (
u
n
) như sau:
u
n
:
n
1
+
n
2
+
n
4
,
∀
n
1
,
2
.
.
.
Tính giới hạn
lim
n...
Đọc tiếp
Cho dãy số ( u n ) như sau: u n : n 1 + n 2 + n 4 , ∀ n = 1 , 2 . . . Tính giới hạn lim n → + ∞ ( u 1 + u 2 + . . . + u n )
A. 1 4
B.1
C. 1 2
D. 1 3
Cho dãy số (
u
n
) như sau:
u
n
n
1
+
n
2
+
n
4
,
∀
n
1
,
2
,
....
Đọc tiếp
Cho dãy số ( u n ) như sau: u n = n 1 + n 2 + n 4 , ∀ n = 1 , 2 , . . . Tính giới hạn lim x → + ∞ ( u 1 + u 2 + . . . + u n ) .
A. 1 4
B. 1
C. 1 2
D. 1 3
Cho n1+n2+n3+n4+n5+n6+n7+n8+n9=18
Trong đó n1;n2;n3;n4;n5;n6;n7;n8;n9 là các số nguyên liên tiếp
Tìm tích C=n1.n2.n3.n4.n5.n6.n7.n8.n9
a) Cho a,b,c ϵ Z. CMR:a3 + b3 + c3 ⋮ 6⇔a +b +c ⋮ 6
b) CM: n2 + n2⋮12 ∀n ϵ Z
c) CM:n(n+2)(25n2-1)⋮24 ∀ n ϵZ
LÀM ƠN NHANH HỘ MK VỚIIIIIIIIIIIIIIIIIIII