Fun tí: Chứng minh định lý Pitago ![]()

Chứng minh định lý PItago
Nhat_Minh.docx
Bạn vào đây nha có đầy đủ hết
Chúc bn hok tốt!!!
Mk thíu bạn vào thống kê hỏi đáp của mk để lấy link nhoa!!!
trong hình vuông lớn của hai cạnh bên trái, mỗi hình vuông chứa bốn tam giác vuông bằng nhau sự khác nhau giữa hai hình vuông này là các tam giác vuông được bố trí khác nhau. Do vậy, khoảng trắng bên trong mỗi hình vuông phải có diện tích bằng nhau. Dựa vào hình vẽ, hai vùng trắng có diện tích bằng nhau cho phép rút ra được kết luận của định lý Pytago.
Chứng minh định lý PITAGO?
trg tam giác vuông
2 cạnh góc vuông là a,b
cạnh huyền: c
a^2+b^2=c^2
#)Giải : (Có rất rất nhiều cách nhưng mk sẽ làm 1 thôi nhé)
Ta có : SADEF = SBCPQ + 4SABC
=> (b + c)2 = a2 + 4.bc/2
=> b2 + 2bc + c2 = a2 + 2bc
=> b2 + c2 = a2 (đpcm)
Gọi ABC là tam giác với các cạnh a, b, và c, với a2 + b2 = c2. ... Một hệ quả của định lý Pytago đảo đó là cách xác định đơn giản một tam giác có là tam giác vuông hay không, hay nó là tam giác nhọn hoặc tam giác tù.
Phát biểu và chứng minh định lý pitago và tiên đề Ơclit
PS:đang cần gấp
Hai tam giác ABC, A'B'C' vuông tại A và A' có AB = A'B', AC > A'C'. Không sử dụng định lý Pitago, chứng minh rằng BC > B'C'
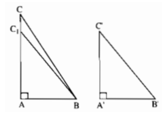
Do AC > A'C' nên lấy được điểm C1 trên cạnh AC sao cho AC1=A′C′. Ta có tam giác vuông ABC1 bằng tam giác vuông A'B'C', suy ra B′C′=BC1. Mặt khác hai đường xiên BC và BC1 kẻ từ B đến đường thẳng AC lần lượt có hình chiếu trên AC là AC và AC1. Vì AC > AC1 nên BC > BC1. Suy ra BC > B'C'.
Cho tam giác ABC vuông tại A.Từ định lý Pitago chứng minh rằng trong ba cạnh AB, AC ,BC thì BC là cạnh lớn nhất.
Theo định lý Pytago, tam giác ABC ( Góc A=90 độ ) có:
\(BC^2=AB^2+AC^2\)
Mà AB, BC, AC > 0 nên BC2 > AB2, BC2 > AC2 hay BC > AB và AC suy ra BC lớn nhất
Khái niệm định lý pitago
Định lý Pitago là một định lý toán học căn bản trong hình học. Định lý Pitago được phát biểu là trong một tam giác vuông bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông. Vậy ở bất kì 1 tam giác vuông nào thì bình phương cạnh huyền luôn bằng tổng bình phương hai cạnh góc vuông.
Tham khảo:
https://loigiaihay.com/ly-thuyet-dinh-li-pytago-c42a5134.htm
định lý pitago là j ?
ĐỊNH LÍ PITAGO VÀ ĐỊNH LÝ PITAGO ĐẢO
➡có pn nnào bít mấy bài toán lớp 7 liên quan tới hai cái định lý đó thì đăng lên giùm mik nha hoặc gửi tin nhắn cg đc .
OOLM ĐỪNG XOÁ. EM ĐANG CẦN GẤP LẮM !
a) Hai tam giác ABC, A'B'C' vuông tại A và A' có AB = A'B', AC > A'C'. Không sử dụng định lí Pitago, chứng minh rằng BC > B'C'
b) Hai tam giác ABC, A'B'C' vuông tại A và A' có AB = A'B', BC > B'C'. Không sử dụng định lí Pitago, chứng minh rằng AC > A'C'
a: Do AC > A'C' nên lấy được điểm C1 trên cạnh AC sao cho AC1=A′C′.
Ta có ΔABC1=ΔA'B'C'
Suy ra B′C′=BC1
Mặt khác hai đường xiên BC và BC1 kẻ từ B đến đường thẳng AC lần lượt có hình chiếu trên AC là AC và AC1.
Vì AC > AC1 nên BC > BC1.
Suy ra BC > B'C'.
b:
-Giả sử AC<A'C'.
Khi đó theo chứng minh câu a) ta có BC < B'C'. Điều này không đúng với giả thiết BC > B'C'.
Giả sử AC=A'C'. Khi đó ta có ΔABC=ΔA'B'C' (c.g.c).
Suy ra BC=B'C'.
Điều này cũng không đúng với giả thiết BC>B'C'. Vậy ta phải có AC>A'C'.