Cho hình thoi ABCD cạnh a,góc A bằng 60 độ
a. Tính \(\overrightarrow{|AC|}\)
b.H là hình chiếu của A lên BC . Tính \(\overrightarrow{|AH|}\)

Những câu hỏi liên quan
Cho hình thoi ABCD cạnh a,góc A bằng 60 độ
a. Tính −−−→|AC||AC|→
b.H là hình chiếu của A lên BC . Tính −−−→|AH||AH|→
Cho hình thoi ABCD đi có cạnh bằng a và có góc A bằng \(60^\circ \). Tìm độ dài của các vectơ sau: \(\overrightarrow p = \overrightarrow {AB} + \overrightarrow {AD} ;\overrightarrow u = \overrightarrow {AB} - \overrightarrow {AD} ;\overrightarrow v = 2\overrightarrow {AB} - \overrightarrow {AC} \).

+) ABCD là hình thoi nên cũng là hình bình hành
Áp dụng quy tắc hình bình hành ta có:
\(\overrightarrow p = \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
\(\Rightarrow |\overrightarrow p| = | \overrightarrow {AC}| =AC \)
+) \(\overrightarrow u = \overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {DB} \)
\(\Rightarrow |\overrightarrow u| = | \overrightarrow {DB}| =DB\)
+) \(\overrightarrow v = 2\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {AB} + \left( {\overrightarrow {AB} - \overrightarrow {AC} } \right) = \overrightarrow {AB} + \overrightarrow {CB} \)\( = \overrightarrow {AB} + \overrightarrow {DA} = \overrightarrow {DB} \)
\(\Rightarrow |\overrightarrow v| = | \overrightarrow {DB}| =DB\)
+ Tính \(AC, DB\)
Tam giác ABD có \(AB=AD=a, \widehat A = 60^o\) nên nó là tam giác đều. Do đó DB = a.
Gọi O là giao điểm hai đường chéo.
Ta có: \(AO = AB. \sin B = a. \sin 60^o = \frac {a \sqrt 3}{2} \Rightarrow AC = a \sqrt 3\)
Vậy \(|\overrightarrow p| = a \sqrt 3 ,|\overrightarrow u| = a, |\overrightarrow v| = a.\)
Đúng 0
Bình luận (0)
Cho hình thoi ABCD tâm O, có cạnh bằng a, góc A 60 độ.
1. Tình \(\left|\overrightarrow{AB}+\overrightarrow{AD}\right|\)
2. Tính \(\left|2\overrightarrow{OB}-3\overrightarrow{OC}\right|\)
Cho hình vuông ABCD có cạnh bằng 1. Tính độ dài các vectơ sau:
a) \(\overrightarrow a = \left( {\overrightarrow {AC} + \overrightarrow {BD} } \right) + \overrightarrow {CB} ;\)
b) \(\overrightarrow a = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {BC} + \overrightarrow {DA} .\)
a) \(\begin{array}{l}\overrightarrow a = \left( {\overrightarrow {AC} + \overrightarrow {BD} } \right) + \overrightarrow {CB} = \left( {\overrightarrow {AC} + \overrightarrow {CB} } \right) + \overrightarrow {BD} \\ = \overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD}\\ \Rightarrow |{\overrightarrow a}|= \left| {\overrightarrow {AD} } \right| = AD = 1\end{array}\)
b) \(\begin{array}{l}\overrightarrow a = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {BC} + \overrightarrow {DA} = \left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) + \left( {\overrightarrow {AD} + \overrightarrow {DA} } \right)\\ = \overrightarrow {AC} + \overrightarrow {AA} = \overrightarrow {AC} + \overrightarrow 0 = \overrightarrow {AC} \end{array}\)
\(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{1^2} + {1^2}} = \sqrt 2 \)
\(\Rightarrow |{\overrightarrow a}|= \left| {\overrightarrow {AC} } \right| = \sqrt 2 \)
Đúng 0
Bình luận (0)
Cho hình thoi ABCD cạnh a, \(\widehat{BCD}\)= 60o . O là giao điểm của AC và BD . Tính \(\left|\overrightarrow{AB}+\overrightarrow{AD}\right|,\left|\overrightarrow{CB}+\overrightarrow{DC}\right|\)
Cho hình thang ABCD có \(\overrightarrow{2AB}=\overrightarrow{DC}\),AC=8,BD=6,góc tạo bởi 2 vecto \(\overrightarrow{AC}\) và \(\overrightarrow{BD}\) bằng 120.Tính độ dài các cạnh AD,BC
Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh bằng a, hình chiếu vuông góc của S lên mặt phẳng đáy là điểm H sao cho :
overrightarrow{AH}dfrac{1}{3}overrightarrow{AC};SHdfrac{4}{3}a
a) Tính thể tích khối chóp S.ABCD
b) Gọi AI là đường cao của tam giác ASC. Chứng minh rằng I là trung điểm của SC và tính thể tích khối tứ diện ABSI ?
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh bằng a, hình chiếu vuông góc của S lên mặt phẳng đáy là điểm H sao cho :
\(\overrightarrow{AH}=\dfrac{1}{3}\overrightarrow{AC};SH=\dfrac{4}{3}a\)
a) Tính thể tích khối chóp S.ABCD
b) Gọi AI là đường cao của tam giác ASC. Chứng minh rằng I là trung điểm của SC và tính thể tích khối tứ diện ABSI ?

\(V_{ABSI}=V_{S.ABI}=\dfrac{1}{2}V_{S.ABCD}=\dfrac{a^3}{9}\)
Đúng 0
Bình luận (0)
cho hình vuông ABCD cạnh a . Tính P=\(( \overrightarrow{AB}+ \overrightarrow{AC})( \overrightarrow{BC}+ \overrightarrow{BD}+ \overrightarrow{BA})\)
Do ABCD là hình vuông nên AC vuông góc BD
Do đó:
\(P=\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\left(\overrightarrow{BC}+\overrightarrow{BA}+\overrightarrow{BD}\right)=\left(\overrightarrow{AB}+\overrightarrow{AC}\right).2\overrightarrow{BD}\)
\(=2\overrightarrow{AB}.\overrightarrow{BD}+2\overrightarrow{AC}.\overrightarrow{BD}=2\overrightarrow{AB}.\overrightarrow{BC}=2a.a.cos135^0=-a^2\sqrt{2}\)
Đúng 0
Bình luận (0)
Cho hình vuông ABCD có cạnh bằng a. Tính các tích vô hướng:
\(\overrightarrow {AB} .\overrightarrow {AD} ,\overrightarrow {AB} .\overrightarrow {AC} ,\overrightarrow {AC} .\overrightarrow {CB} ,\overrightarrow {AC} .\overrightarrow {BD} \)
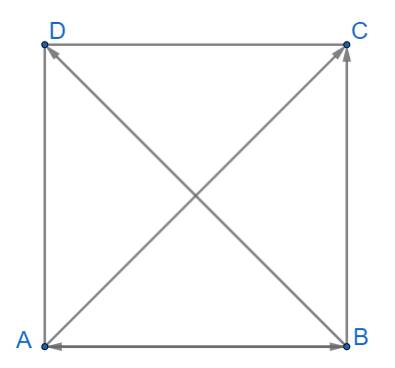
Ta có: \(AC = BD = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
+) \(AB \bot AD \Rightarrow \overrightarrow {AB} \bot \overrightarrow {AD} \Rightarrow \overrightarrow {AB} .\overrightarrow {AD} = 0\)
+) \(\overrightarrow {AB} .\overrightarrow {AC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = a.a\sqrt 2.\cos 45^\circ = a^2\)
+) \(\overrightarrow {AC} .\overrightarrow {CB} = \left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {CB} } \right|.\cos \left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right) = a\sqrt 2 .a.\cos 135^\circ = - {a^2}\)
+) \(AC \bot BD \Rightarrow \overrightarrow {AC} \bot \overrightarrow {BD} \Rightarrow \overrightarrow {AC} .\overrightarrow {BD} = 0\)
Chú ý
\(\overrightarrow {a} \bot \overrightarrow {b} \Leftrightarrow \overrightarrow {a} .\overrightarrow {b} = 0\)
Đúng 0
Bình luận (0)











