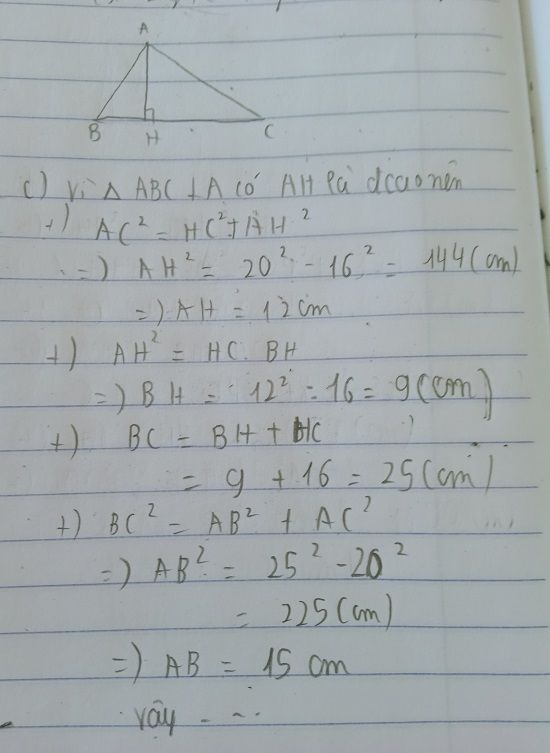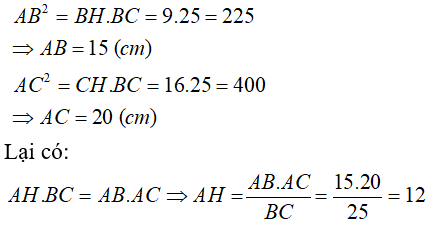Cho tam giác abc vuông tại A , đường cao AH , AB = 24 cm , BC = 30 cm . tính AC AH BH CH

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, đường cao AH .
a) Biết AH = 12cm ,CH = 5cm.Tính AC , AB , BC , BH
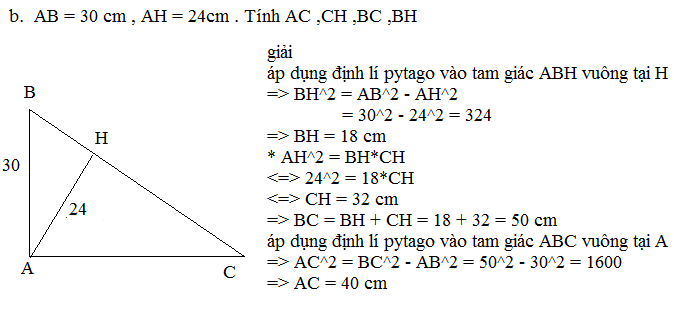
b) Biết AB = 30 cm, AH = 24 cm. Tính AC ,CH ,BC ,BH
c) Biết AC = 20 cm , CH = 16 cm. Tính AB ,AH,BC,BH
d) Biết AB = 6 cm , BC = 10 cm . Tính AC, AH, BH, CH
e) Biết BH =9 cm, CH = 16 cm . Tính AC , AB, BC, AH
Giúp mìn với ạ, cảm ơn nhìu
Cho tam giác ABC vuông tại A, đường cao AH .
a) Biết AH = 12cm ,CH = 5cm.Tính AC , AB , BC , BH
b) Biết AB = 30 cm, AH = 24 cm. Tính AC ,CH ,BC ,BH
c) Biết AC = 20 cm , CH = 16 cm. Tính AB ,AH,BC,BH
d) Biết AB = 6 cm , BC = 10 cm . Tính AC, AH, BH, CH
e) Biết BH =9 cm, CH = 16 cm . Tính AC , AB, BC, AH
Bài 1: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AH24 cm và HC18 cm.
Tính: BH, ,BC,AC,AB và diện tích tam giác ABC
Bài 2: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB 12 cm và BC20 cm.
Tính: BH, ,AC,HC,AH và diện tích tam giác ABC
Bài 3: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB3 cm và AC4 cm.
Tính: BH, ,BC,HC,AH và diện tích tam giác ABC
Bài 4: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AC15 cm và AH 12 cm.
Tính: BH, ,BC,A...
Đọc tiếp
Bài 1: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AH=24 cm và HC=18 cm. Tính: BH, ,BC,AC,AB và diện tích tam giác ABC Bài 2: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB= 12 cm và BC=20 cm. Tính: BH, ,AC,HC,AH và diện tích tam giác ABC Bài 3: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB=3 cm và AC=4 cm. Tính: BH, ,BC,HC,AH và diện tích tam giác ABC Bài 4: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AC=15 cm và AH =12 cm. Tính: BH, ,BC,AB,AH và diện tích tam giác ABC Bài 5:Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB=20 cm và HC=9cm. Tính: BH, ,BC,AC,AH và diện tích tam giác ABC
Bài 5:
Ta có: \(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH\left(BH+9\right)=400\)
\(\Leftrightarrow BH^2+25HB-16HB-400=0\)
\(\Leftrightarrow BH=16\left(cm\right)\)
hay BC=25(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AC=15\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)
Đúng 3
Bình luận (0)
Cho tam giác ABC vuông tại A có AB = 30 cm, Vẽ đường cao AH , AH = 24 cm
a) Tính BH ; BC ; AC
b) Đường thẳng vuông góc với AB tại B cắt tia AH tại D. Tính BD
đừng bắt trc t hiếu à , m càng ngày càng giống t rồi đấy , đờ mờ
Đúng 0
Bình luận (0)
ĐCM lũ tụi m :(((( Ko giúp mà vô phá cả 2 tk pain ôi cái chuyện j xảy ra vậy
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A, đường cao AH.
a) Biết AH = 6 cm; BH = 4,5 cm. Tính AB, AC, BC, HC.
b) Biết AB = 6 cm, BH = 3 cm. Tính AH, AC, CH
a,
pytago trong tam giác ABH
\(=>AB=\sqrt{AH^2+BH^2}=\sqrt{6^2+4,5^2}=7,5cm\)
dễ dàng chứng minh \(\Delta AHB\sim\Delta CAB\left(g.g\right)=>\dfrac{AH}{AC}=\dfrac{HB}{AB}=>AC=10cm\)
pytago cho tam giác ABC
\(=>BC=\sqrt{AB^2+AC^2}=12,5cm\)
\(=>HC=BC-HB=8cm\)
b, pytago cho tam giác AHB
\(=>AH=\sqrt{AB^2-BH^2}=3\sqrt{3}cm\)
rồi tính AC , CH làm tương tự bài trên
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH, biết AB = 6 cm AC = 8 cm .Tính BC, AH, CH, BH
\(BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\\ \left\{{}\begin{matrix}AH=\dfrac{AB\cdot AC}{BC}=4,8\left(cm\right)\\CH=\dfrac{AC^2}{BC}=6,4\left(cm\right)\\BH=\dfrac{AB^2}{BC}=3,6\left(cm\right)\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Áp dụng PTG ta có: \(AB^2+AC^2=BC^2\Rightarrow BC=\sqrt{6^2+8^2}=10\)
Áp dụng HTL ta có: \(AB.AC=AH.BC\Rightarrow AH=\dfrac{6.8}{10}=4,8\)
Áp dụng HTL ta có:\(BH.BC=AB^2\Rightarrow BC=\dfrac{6^2}{10}=3,6\)
Áp dụng HTL ta có:\(CH.BC=AC^2\Rightarrow BC=\dfrac{8^2}{10}=6,4\)
Đúng 1
Bình luận (0)
cho tam giác vuông ABC vuông tại A sao cho đường cao AH biết AB= 3 cm , AC = 4 cm , tính BC AH BH CH
Áp dụng định lý Pytago vào tam giác ABC(góc A=90) có:
BC2=AB2+AC2
<=>BC2=32+42
<=>BC2=25
<=>BC=5(cm)
Áp dụng HTL vào tam giác ABC vuông tại A có đường cao AH được:
AB.AC=BC.AH
<=>3.4=5.AH
<=> AH=\(\dfrac{3.4}{5}\)
<=>AH=2,4(cm)
Áp dụng định lý Pytago vào tam giác AHB vuông tại H có:
AB2=AH2+BH2
<=>BH2=32-2,42
<=>BH2=3,24
<=>BH=1,8(cm)
Ta có:BC=BH+CH
=>CH=BC-BH=5-1,8=3,2(cm)
Vậy BC=5cm;AH=2,4cm;BH=1,8cm;CH=3,2cm
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A , đường cao AH
1. Biết AB = 18 cm , AC =24 cm .
a, Tính BC , BH , AH .
b, Tính các góc của tam giác ABC.
2. Kẻ HE vuông góc với AB , HF vuông góc với AC .
Chứng minh AE.EB+À.FC = AH 2
Bài 1:
a: BC=30cm
AH=14,4(cm)
BH=10,8(cm)
Đúng 0
Bình luận (0)
Bài 3: Cho tam giác ABC vuông tại A có AH là đường cao, BH = 9 cm, CH = 16 cm. Tính BC, AH, AB, AC
Ta có: BC=BH+CH
nên BC=25(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=15\left(cm\right)\\AC=20\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB: 12cm, AH:7,2 cm. tính AC BC BH CH
Áp dụng HTL:
\(\dfrac{1}{AH^2}=\dfrac{1}{51,84}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{1}{144}+\dfrac{1}{AC^2}\\ \Rightarrow\dfrac{1}{AC^2}=\dfrac{1}{81}\Rightarrow AC=9\left(cm\right)\)
Áp dụng PTG \(BC=\sqrt{BA^2+AC^2}=15\left(cm\right)\)
Áp dụng HTL:
\(\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=9,6\left(cm\right)\\CH=\dfrac{AC^2}{BC}=5,4\left(cm\right)\end{matrix}\right.\)
Đúng 2
Bình luận (0)