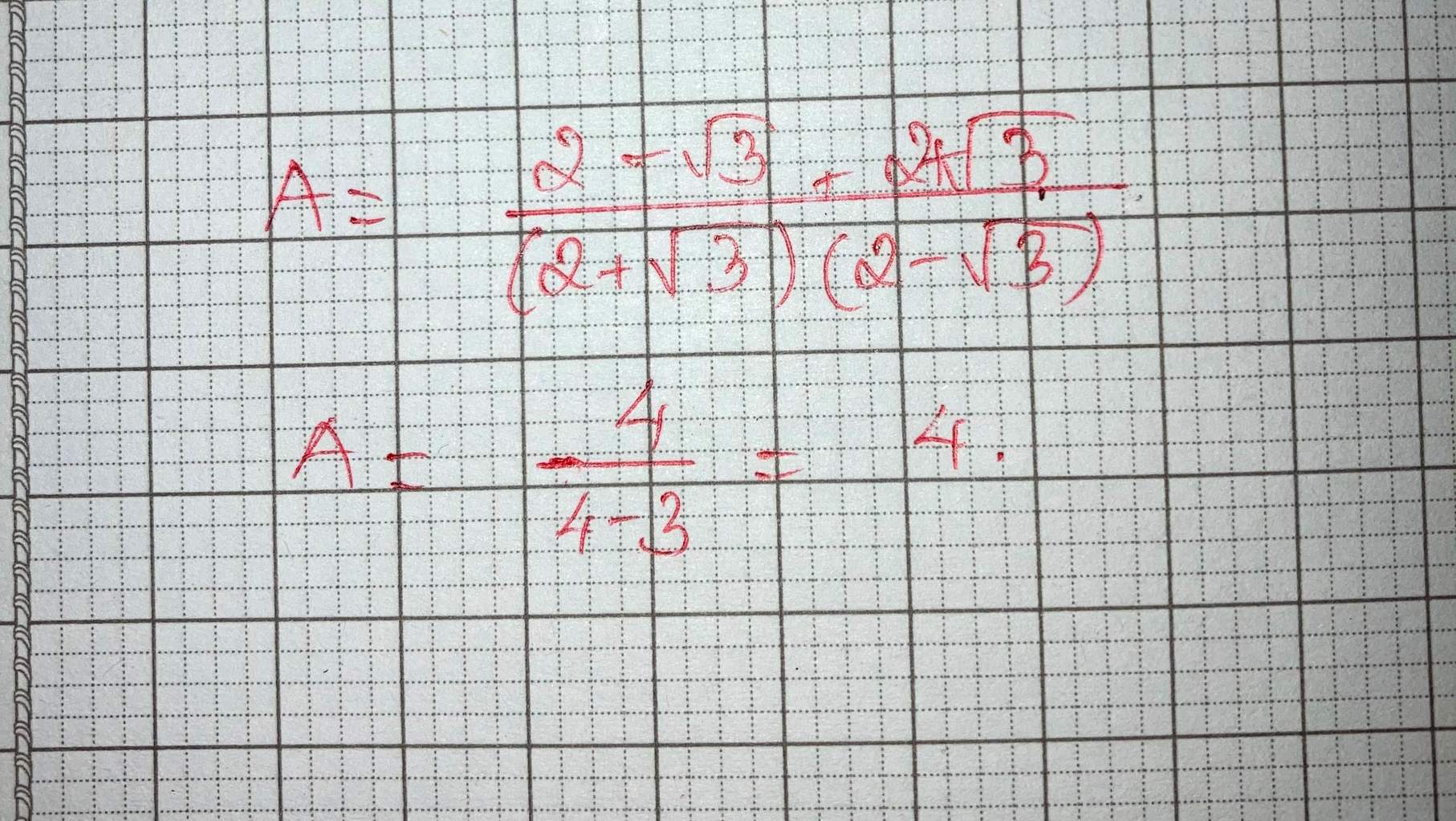a.Chứng tỏ rằng B = 1/2² + 1/3² + 1/4² + 1/5² + 1/6² + 1/7² +1/8² < 1

b.Cho S = 3/1.4 + 3/4.7 + 3/7.10 +......+3/40.43 + 3/43.46 hãy chứng tỏ rằng S < 1

Sửa đề: 1/3²=1/2³

Giải:

A=1+1/2+1/2²+1/2³+..1/2²⁰¹²

2A=2+1+1/2+1/2²+...+1/2²⁰¹¹

2A-A=(2+1+1/2+1/2²+...+1/2²⁰¹¹)-(1+1/2+1/2²+1/2³+...+1/2²⁰¹²)

A=2-2²⁰¹²

Chúc bạn học tốt!

\(S=1-2+2^2-2^3+...+2^{2012}-2^{2013}\)

\(\Rightarrow2S=2-2^2+2^3-2^4+...+2^{2013}-2^{2014}\)

\(\Rightarrow2S+S=2-2^2+2^3-...-2^{2014}+1-2^2-2^3+...-2^{2013}\)

\(\Rightarrow3S=1-2^{2014}\)\(\Rightarrow3S-2^{2014}=1-2^{2015}\)

Đặt N = 1 + 2 + 2² +...+ 2²⁰¹²

2N = 2 + 2² + 2³ +...+ 2²⁰¹³

2N - N = (2 + 2² + 2³+....+ 2²⁰¹³) - (1 + 2 + 2² +....+ 2²⁰¹²)

N = 2²⁰¹³ - 1

Thay N vào M ta được:

Đặt \(N=1+2+2^2+...+2^{2012}\)

\(2N=2+2^2+2^3+...+2^{2013}\)

\(2N-N=\left(2+2^2+2^3+...+2^{2013}\right)-\left(1+2+2^2+...+2^{2012}\right)\)

\(N=2^{2013}-1\)

Thay N vào M ta được:

\(M=\dfrac{2^{2013-1}}{2^{2014}-2}=\dfrac{2^{2013}-1}{2\left(2^{2013}-1\right)}=\dfrac{1}{2}\)

Tham khảo link: https://olm.vn/hoi-dap/detail/80564627052.html

\(\left(3-1\right)A=\left(3-1\right)\left(3+1\right)\left(3^2+1\right)\left(3^4+1\right)...\left(3^{64}+1\right)\\ 2A=\left(3^2-1\right)\left(3^2+1\right)\left(3^4+1\right)...\left(3^{64}+1\right)\\ 2A=\left(3^4-1\right)\left(3^4+1\right)...\left(3^{64}+1\right)\\ 2A=\left(3^8-1\right)\left(3^8+1\right)...\left(3^{64}-1\right)\\ ...\\ 2A=\left(3^{64}-1\right)\left(3^{64}+1\right)\\ 2A=3^{128}-1\)

Vậy \(A=\dfrac{3^{128}-1}{2}.\)

\(A=1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{2012}}\)

=>2A=\(2+1+\frac{1}{2}+...+\frac{1}{2^{2011}}\)

=>2A-A=\(\left(2+1+\frac{1}{2}+...+\frac{1}{2^{2011}}\right)-\left(1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{2012}}\right)=2-\frac{1}{2^{2012}}\)

=>A=\(\frac{2^{2013}-1}{2^{2012}}\)

`A=1/[\sqrt{3}+1]+1/[\sqrt{3}-1]`

`A=[\sqrt{3}-1+\sqrt{3}+1]/[3-1]`

`A=[2\sqrt{3}]/2=\sqrt{3}`

\(A=\dfrac{1}{\sqrt{3+1}}+\dfrac{1}{\sqrt{3-1}}\)

\(A=\dfrac{\sqrt{3-1+\sqrt{3+1}}}{\left(\sqrt{3+1}\right)\left(\sqrt{3-1}\right)}\)

\(A=\dfrac{2\sqrt{3}}{3-1}\)

\(A=\dfrac{2\sqrt{3}}{2}\)

\(A\sqrt{3}\)

\(A=\dfrac{1}{\sqrt{3}+1}+\dfrac{1}{\sqrt{3}-1}\)

\(A=\dfrac{\sqrt{3}-1+\sqrt{3}+1}{3-1}\)

\(A=\dfrac{2\sqrt{3}}{2}\)

\(A=\sqrt{3}\)

\(A=\dfrac{x+2+x-1-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)

\(=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)