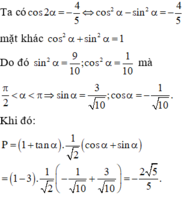1: 

a: sin a=căn 3/2

\(cosa=\sqrt{1-sin^2a}=\sqrt{1-\dfrac{3}{4}}=\sqrt{\dfrac{1}{4}}=\dfrac{1}{2}\)

\(tana=\dfrac{\sqrt{3}}{2}:\dfrac{1}{2}=\sqrt{3}\)

cot a=1/tan a=1/căn 3

b: \(tana=2\)

=>cot a=1/tan a=1/2

\(1+tan^2a=\dfrac{1}{cos^2a}\)

=>\(\dfrac{1}{cos^2a}=5\)

=>cos^2a=1/5

=>cosa=1/căn 5

\(sina=\sqrt{1-cos^2a}=\sqrt{\dfrac{4}{5}}=\dfrac{2}{\sqrt{5}}\)

c: \(cosa=\sqrt{1-\left(\dfrac{5}{13}\right)^2}=\dfrac{12}{13}\)

tan a=5/13:12/13=5/12

cot a=1:5/12=12/5

Ta dễ có hệ: \(\hept{\begin{cases}\sin\alpha+\cos\alpha=\sqrt{2}\\\sin^2\alpha+\cos^2\alpha=1\end{cases}}\)

Đặt \(\sin\alpha=x;\cos\alpha=y\)thì hệ trở thành \(\hept{\begin{cases}x+y=\sqrt{2}\\x^2+y^2=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x+y=\sqrt{2}\\\left(x+y\right)^2-2xy=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x+y=\sqrt{2}\\xy=\frac{1}{2}\end{cases}}\)

x, y là nghiệm của phương trình \(t^2-\sqrt{2}t+\frac{1}{2}=0\Leftrightarrow\left(t-\frac{1}{\sqrt{2}}\right)^2=0\Leftrightarrow t=\frac{1}{\sqrt{2}}\)

\(\Rightarrow x=y=\frac{1}{\sqrt{2}}\)hay \(\sin\alpha=\cos\alpha=\frac{1}{\sqrt{2}}\)suy ra \(\tan\alpha=\cot\alpha=1\)

1.

\(\frac{\pi}{2}< x< \pi\\ \Rightarrow cosx< 0,sinx>0,cotx< 0\)

\(cotx=\frac{1}{tanx}=\frac{-1}{3}\)

\(1+tan^2x=\frac{1}{cos^2x}\\ \Rightarrow cosx=\sqrt{\frac{1}{1+tan^2}}=\sqrt{\frac{1}{1+9}}=-\frac{\sqrt{10}}{10}\)

\(sinx=\sqrt{1-cos^2x}=\sqrt{1-\frac{10}{100}}=\frac{3\sqrt{10}}{10}\)

Ta có:

\(\begin{array}{l}\cos {30^o} = \sin \left( {{{90}^o} - {{30}^o}} \right) = \sin {60^o} = \frac{{\sqrt 3 }}{2};\\\sin {150^o} = \sin \left( {{{180}^o} - {{150}^o}} \right) = \sin {30^o} = \frac{1}{2};\\\tan {135^o} =  - \tan \left( {{{180}^o} - {{135}^o}} \right) =  - \tan {45^o} =  - 1\end{array}\)

\( \Rightarrow E = 2.\frac{{\sqrt 3 }}{2} + \frac{1}{2} - 1 = \sqrt 3  - \frac{1}{2}.\)

\(\pi< x< \dfrac{3\pi}{2}\Rightarrow\left\{{}\begin{matrix}sinx< 0\\cosx< 0\end{matrix}\right.\)

\(\Rightarrow sinx=-\sqrt{1-cos^2x}=-\dfrac{4}{5}\)

\(\Rightarrow tanx=\dfrac{sinx}{cosx}=\dfrac{4}{3}\) ; \(cotx=\dfrac{1}{tanx}=\dfrac{3}{4}\)

\(P=\dfrac{4}{3}+\dfrac{3}{4}=\dfrac{25}{12}\)

Đáp án đúng : B

\(tana-cota=2\sqrt{3}\Rightarrow\left(tana-cota\right)^2=12\)

\(\Rightarrow\left(tana+cota\right)^2-4=12\Rightarrow\left(tana+cota\right)^2=16\)

\(\Rightarrow P=4\)

\(sinx+cosx=\dfrac{1}{5}\Rightarrow\left(sinx+cosx\right)^2=\dfrac{1}{25}\)

\(\Rightarrow1+2sinx.cosx=\dfrac{1}{25}\Rightarrow sinx.cosx=-\dfrac{12}{25}\)

\(P=\dfrac{sinx}{cosx}+\dfrac{cosx}{sinx}=\dfrac{sin^2x+cos^2x}{sinx.cosx}=\dfrac{1}{sinx.cosx}=\dfrac{1}{-\dfrac{12}{25}}=-\dfrac{25}{12}\)