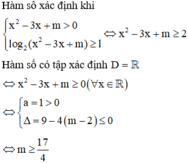tìm m để hàm số y= \(\frac{x^2-4x+1}{x^3-6x^2+11x-m}\) có tập xác định D=R\{a;b;c} ; a\(\ne b\ne c\) đồngthời thõa mãn điều kiện a<b<c; a+c=2b

Những câu hỏi liên quan
Bài 1: Tìm tập hợp các giá trị của m để hàm số \(y=\sqrt{\left(m+10\right)x^2-2\left(m-2\right)x+1}\)có tập xác định D= R
Bài 2:Có bao nhiêu giá trị m nguyên để hàm số \(y=1-\sqrt{\left(m+1\right)x^2-2\left(m-1\right)x+2-2m}\)có tập xác định là R?
Tìm tập hợp các giá trị của m để hàm số y=√ ( m - 2)x^2 - 2( m- 3)x + m - 1 có tập xác định là R
Hàm số xác định \(\Leftrightarrow\left(m-2\right)x^2-2\left(m-3\right)x+m-1\ge0\)
Đặt \(f\left(x\right)=\left(m-2\right)x^2-2\left(m-3\right)x+m-1\ge0\)
\(f\left(x\right)\ge0,\forall x\in R\Leftrightarrow\left\{{}\begin{matrix}a>0\\\Delta\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m-2>0\\\left[-2\left(m-3\right)\right]^2-4\left(m-2\right)\left(m-1\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>2\\4\left(m^2-6m+9\right)-4\left(m^2-3m+2\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow4m^2-24m+36-4m^2+12m-8\le0\)
\(\Leftrightarrow-12m+28\le0\)
\(\Leftrightarrow m\le\dfrac{7}{3}\)
\(KL:m\in(2;\dfrac{7}{3}]\)
Đúng 2
Bình luận (0)
Tìm tất cả các giá trị của m để hàm số sau xác định trên R:
a, ydfrac{x+3}{left(2m-4right)x+m^2-9}
b, ydfrac{x+3}{x^2-2left(m-3right)x+9}
c, ydfrac{x+3}{sqrt{x^2+6x+2m-3}}
d, ydfrac{x+3}{sqrt{-x^2+6x+2m-3}}
e, ydfrac{x+3}{sqrt{x^2+2left(m-1right)x+2m-2}}
Đọc tiếp
Tìm tất cả các giá trị của m để hàm số sau xác định trên R:
a, \(y=\dfrac{x+3}{\left(2m-4\right)x+m^2-9}\)
b, \(y=\dfrac{x+3}{x^2-2\left(m-3\right)x+9}\)
c, \(y=\dfrac{x+3}{\sqrt{x^2+6x+2m-3}}\)
d, \(y=\dfrac{x+3}{\sqrt{-x^2+6x+2m-3}}\)
e, \(y=\dfrac{x+3}{\sqrt{x^2+2\left(m-1\right)x+2m-2}}\)
Hàm số xác định trên R khi và chỉ khi:
a.
\(\left(2m-4\right)x+m^2-9=0\) vô nghiệm
\(\Leftrightarrow\left\{{}\begin{matrix}2m-4=0\\m^2-9\ne0\end{matrix}\right.\) \(\Rightarrow m=2\)
b.
\(x^2-2\left(m-3\right)x+9=0\) vô nghiệm
\(\Leftrightarrow\Delta'=\left(m-3\right)^2-9< 0\)
\(\Leftrightarrow m^2-6m< 0\Rightarrow0< m< 6\)
c.
\(x^2+6x+2m-3>0\) với mọi x
\(\Leftrightarrow\Delta'=9-\left(2m-3\right)< 0\)
\(\Leftrightarrow m>6\)
e.
\(-x^2+6x+2m-3>0\) với mọi x
Mà \(a=-1< 0\Rightarrow\) không tồn tại m thỏa mãn
f.
\(x^2+2\left(m-1\right)x+2m-2>0\) với mọi x
\(\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(2m-2\right)=m^2-4m+3< 0\)
\(\Leftrightarrow1< m< 3\)
Đúng 0
Bình luận (0)
Bài 1 : Cho hàm số y 3(2mx - 1) + m + 2 (d)a. Vẽ đồ thị hàm số với m dfrac{1}{2}b. Tìm m để hàm số nghịch biến trên tập xác định.c. Tìm m để (d) vuông góc với đường thẳng (△) : y 6x + 1d. Tìm điểm cố định luôn nằm trên đường thẳng (d).e. Tìm khoảng cách lớn nhất từ gốc tọa độ O đên (d). Bài 2 : Cho hàm số y 3m - m - 1 (d)a. Vẽ đồ thị hàm số với m -1.b. Tìm m để hàm số vuông góc với đường thẳng (△) : y x + 1.c. Tìm m để đồ thị hàm số cắt trục tung tại điểm có tung độ là 2.d. Tìm điểm cố địn...
Đọc tiếp
Bài 1 : Cho hàm số y = 3(2mx - 1) + m + 2 (d)
a. Vẽ đồ thị hàm số với m = \(\dfrac{1}{2}\)
b. Tìm m để hàm số nghịch biến trên tập xác định.
c. Tìm m để (d) vuông góc với đường thẳng (△) : y = 6x + 1
d. Tìm điểm cố định luôn nằm trên đường thẳng (d).
e. Tìm khoảng cách lớn nhất từ gốc tọa độ O đên (d).
Bài 2 : Cho hàm số y = 3m - m - 1 (d)
a. Vẽ đồ thị hàm số với m = -1.
b. Tìm m để hàm số vuông góc với đường thẳng (△) : y = x + 1.
c. Tìm m để đồ thị hàm số cắt trục tung tại điểm có tung độ là 2.
d. Tìm điểm cố định luôn nằm trên (d).
e. Tìm m để khoảng cách từ gốc tọa độ O đến đường thẳng (d) là lớn nhất.
Bài 3 : Cho hàm số y = (4m - 3)x + m + 3
a. Vẽ đồ thị hàm số với m = 1.
b. Tìm m để hàm số nghịch biên trên tập xác đinh.
c. Tìm m để đồ thị hàm số cắt trục tung tại điểm có tung độ là -4.
d. Tìm điểm cố định luôn nằm trên (d).
e. Tìm m để khoảng cách từ gốc tọa độ O đến đường thẳng (d) là lớn nhất.
c: Để (d) vuông góc với (Δ) thì \(\left(6m+1\right)\cdot6=-1\)
\(\Leftrightarrow6m+1=-\dfrac{1}{6}\)
hay \(m=-\dfrac{7}{36}\)
Đúng 0
Bình luận (0)
Tìm m để các hàm số sau có tập xác định là R (hay luôn xác định trên R):
a. \(y=f\left(x\right)=\dfrac{3x+1}{x^2+2\left(m-1\right)x+m^2+3m+5}\)
b. \(y=f\left(x\right)=\sqrt{x^2+2\left(m-1\right)x+m^2+m-6}\)
c. \(y=f\left(x\right)=\dfrac{3x+5}{\sqrt{x^2-2\left(m+3\right)x+m+9}}\)
a.
\(\Leftrightarrow x^2+2\left(m-1\right)x+m^2+3m+5\ne0\) ; \(\forall x\)
\(\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(m^2+3m+5\right)< 0\)
\(\Leftrightarrow-5m-4< 0\)
\(\Leftrightarrow m>-\dfrac{4}{5}\)
b.
\(\Leftrightarrow x^2+2\left(m-1\right)x+m^2+m-6\ge0\) ;\(\forall x\)
\(\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(m^2+m-6\right)\le0\)
\(\Leftrightarrow-3m+7\le0\)
\(\Rightarrow m\ge\dfrac{7}{3}\)
c.
\(x^2-2\left(m+3\right)x+m+9>0\) ;\(\forall x\)
\(\Leftrightarrow\Delta'=\left(m+3\right)^2-\left(m+9\right)< 0\)
\(\Leftrightarrow m^2+5m< 0\Rightarrow-5< m< 0\)
Đúng 1
Bình luận (1)
y= \(\dfrac{mx}{\sqrt{x-m+2}+1}\)
a, Tìm tập xác định của hàm số theo tham số m
b, Tìm m để hàm số có tập xác định trên (0;1)
1. Tập hợp xác định của hàm số
y = (3x+10 )/(x^2+14x+45) là:
A.R
B.R \ {3; -5; 9}
C.R \ {-5; -9}
D. R \ {5; 9}
2.Hàm số y = √(x+7) + 2/(x^2 + 6x - 16) có tập xác định D bằng
A. [7;+∞)
B. (-7;+∞) \ {-8;2}
C. [-7; 7] \ {2}
D. [-7;+∞) \ {2}
Giúp e nha mọi người
1.Ý C
Hàm số có nghĩa khi \(x^2+14x+45\ne0\Leftrightarrow x\ne\left\{-5;-9\right\}\)
\(\Rightarrow D=R\backslash\left\{-5;-9\right\}\)
2. Ý D
Hàm số có nghĩa khi \(\left\{{}\begin{matrix}x+7\ge0\\x^2+6x-16\ne0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x\ge-7\\x\ne\left\{2;-8\right\}\end{matrix}\right.\)
\(\Rightarrow D=\)\([-7;+ \infty) \)\(\backslash\left\{2\right\}\)
Đúng 2
Bình luận (0)
ĐK : \(x^2+14x+45\ne0\)
\(\Leftrightarrow\hept{\begin{cases}x\ne-5\\x\ne-9\end{cases}}\)
\(TXĐ:D=R\backslash\left\{-5;-9\right\}\)
Chọn C
ĐK : \(\hept{\begin{cases}x+7\ge0\\x^2+6x-16\ne0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x\ge-7\\x\ne-8\\x\ne2\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x\ge-7\\x\ne2\end{cases}}\)
\(TXĐ:D=\left(-7;+\infty\right)\backslash\left\{2\right\}\)
Chọn D
Tìm tập xác định của mỗi hàm số sau:
a) \(y = \frac{1}{{{x^2} - x}}\)
b) \(y = \sqrt {{x^2} - 4x + 3} \)
c) \(y = \frac{1}{{\sqrt {x - 1} }}\)
a) \(y = \frac{1}{{{x^2} - x}}\) xác định \( \Leftrightarrow {x^2} - x \ne 0 \Leftrightarrow \left\{ \begin{array}{l}x \ne 0\\x \ne 1\end{array} \right.\)
Tập xác định \(D = \mathbb{R}\backslash \left\{ {0;1} \right\}\)
b) \(y = \sqrt {{x^2} - 4x + 3} \) xác định \( \Leftrightarrow {x^2} - 4x + 3 \ge 0 \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\x \le 1\end{array} \right.\)
Tập xác định \(D = \left( { - \infty ;1} \right] \cup \left[ {3; + \infty } \right)\)
c) \(y = \frac{1}{{\sqrt {x - 1} }}\) xác định \( \Leftrightarrow x - 1 > 0 \Leftrightarrow x > 1\)
Tập xác định \(D = \left( {1; + \infty } \right)\)
Đúng 1
Bình luận (0)
Cho hàm số
y
log
2
x
2
-
3
x
+
m
-
1
. Tìm m để hàm số có tập xác định D R. A.
m
≤
9
4
B.
m
≤
17...
Đọc tiếp
Cho hàm số y = log 2 x 2 - 3 x + m - 1 . Tìm m để hàm số có tập xác định D = R.
A. m ≤ 9 4
B. m ≤ 17 4
C. m ≥ 17 4
D. m ≥ 9 4