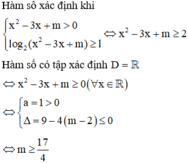Các câu hỏi tương tự
Cho các phát biểu sau(1) Đơn giản biểu thức
M
a
1
4
-
b
1
4
a
1
4
+
b
1...
Đọc tiếp
Cho các phát biểu sau
(1) Đơn giản biểu thức M = a 1 4 - b 1 4 a 1 4 + b 1 4 a 1 2 + b 1 2 ta được M = a - b
(2) Tập xác định D của hàm số y = log 2 ln 2 x - 1 là D = e ; + ∞
(3) Đạo hàm của hàm số y = log 2 ln x là y ' = 1 x ln x . ln 2
(4) Hàm số y = 10 log a x - 1 có đạo hàm tại mọi điểm thuộc tập xác định
Số các phát biểu đúng là
A. 6
B. 1
C. 3
D. 4
Tìm tất cả các giá trị thực của tham số m để hàm số
y
l
n
x
2
-
2
m
x
+
4
có tập xác định D R A. -2 m 2 B. m 2 C.
-
2
≤
m
≤
2
D. m 2 hoặc m -2
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = l n x 2 - 2 m x + 4 có tập xác định D = R
A. -2 < m < 2
B. m < 2
C. - 2 ≤ m ≤ 2
D. m > 2 hoặc m < -2
Cho hàm số
y
1
3
x
3
-
(
m
+
1
)
x
2
+
(
m
+
3
)
x
+
m
-
4
. Tìm m để hàm số yf(|x|) có 5 điểm cực trị A. -3m-1 B. m1 C. m4 D. m0
Đọc tiếp
Cho hàm số y = 1 3 x 3 - ( m + 1 ) x 2 + ( m + 3 ) x + m - 4 . Tìm m để hàm số y=f(|x|) có 5 điểm cực trị
A. -3<m<-1
B. m>1
C. m>4
D. m>0
Cho hàm số yf(x) xác định trên
R
/
2
, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sauTìm tập hợp các giá trị của tham số m để phương trình 2f(x)-m0 có hai nghiệm. A.
(
-
∞
;
-
2
)
∪
(
6
;
+
∞
)
B.
(
-
∞
;
-
6...
Đọc tiếp
Cho hàm số y=f(x) xác định trên R / 2 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau
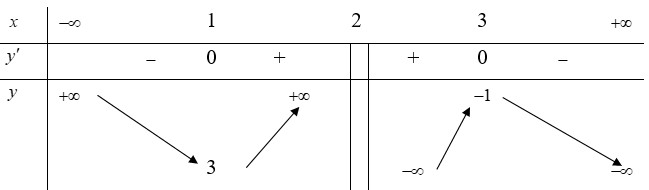
Tìm tập hợp các giá trị của tham số m để phương trình 2f(x)-m=0 có hai nghiệm.
A. ( - ∞ ; - 2 ) ∪ ( 6 ; + ∞ )
B. ( - ∞ ; - 6 ) ∪ ( - 2 ; + ∞ )
C. ( 2 ; 6 )
D. ( - 6 ; - 2 )
Cho hàm số R xác định và liên tục trên D thỏa mãn f(x)3. Biết
(
f
(
x
)
-
3
m
x
-
3
m
2
x
2
-
6...
Đọc tiếp
Cho hàm số R xác định và liên tục trên D thỏa mãn f(x)>3. Biết ( f ( x ) - 3 m x - 3 = m 2 x 2 - 6 m x + 9 + m f 2 ( x ) - 6 f ( x ) + 9 + m với m>0. Tính l o g m f ( m ) ?
A. 2
B. 1
C. 3
D. 4
Cho hàm số R xác định và liên tục trên D thỏa mãn f(x)3. Biết
(
f
(
x
)
-
3
m
x
-
3
m
2
x
2
-
6...
Đọc tiếp
Cho hàm số R xác định và liên tục trên D thỏa mãn f(x)>3. Biết ( f ( x ) - 3 m x - 3 = m 2 x 2 - 6 m x + 9 + m f 2 ( x ) - 6 f ( x ) + 9 + m với m>0. Tính l o g m f ( m ) ?
A. 2
B. 1
C. 3
D. 4
Cho hàm số
y
f
x
xác định, liên tục và có đạo hàm trên đoạn
a
,
b
.
Xét các khẳng định sau: 1. Hàm số
f
x
đồng biến trên
a
;
b
thì
f
x
0
,
∀
x
∈...
Đọc tiếp
Cho hàm số y = f x xác định, liên tục và có đạo hàm trên đoạn a , b . Xét các khẳng định sau:
1. Hàm số f x đồng biến trên a ; b thì f ' x > 0 , ∀ x ∈ a ; b
2. Giả sử f a > f c > f b , ∀ x ∈ a ; b suy ra hàm số nghịch biến trên a ; b
3. Giả sử phương trình f ' x = 0 có nghiệm là x = m khi đó nếu hàm số y = f x đồng biến trên m ; b thì hàm số y = f x nghịch biến trên a , m
4. Nếu f ' x ≥ 0 , ∀ x ∈ a ; b , thì hàm số đồng biến trên a ; b
Số khẳng định đúng trong các khẳng định trên là
A. 1
B. 0
C. 3
D. 2
Cho hàm số yf(x) xác định, liên tục trên R{1} và có bảng biến thiên như sauTìm tập hợp tất cả các giá trị của tham thực m để phương trình f(x)m có nghiệm lớn hơn 2 A.
(
-
∞
;
1
)
B. (3;4) C.
(
1
;
+
∞
)
D.
(
4
;
+
∞
)
Đọc tiếp
Cho hàm số y=f(x) xác định, liên tục trên R\{1} và có bảng biến thiên như sau
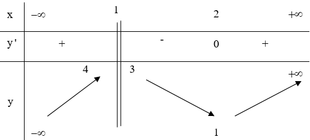
Tìm tập hợp tất cả các giá trị của tham thực m để phương trình f(x)=m có nghiệm lớn hơn 2
A. ( - ∞ ; 1 )
B. (3;4)
C. ( 1 ; + ∞ )
D. ( 4 ; + ∞ )
Tìm tất cả các giá trị của m để đường thẳng d : y x + 4 cắt đồ thị hàm số
y
x
3
+
2
m
x
2
+
(
m
+
3
)
x
+
4
tại 3 điểm phân biệt
A
(
0
;
4
)
và C sao cho diện tích
∆
M
B
C
bằng 4, với M(1;3) A.
m...
Đọc tiếp
Tìm tất cả các giá trị của m để đường thẳng d : y = x + 4 cắt đồ thị hàm số y = x 3 + 2 m x 2 + ( m + 3 ) x + 4 tại 3 điểm phân biệt A ( 0 ; 4 ) và C sao cho diện tích ∆ M B C bằng 4, với M(1;3)
A. m = 2 m = 3
B. m = - 2 m = 3
C. m = 3
D. m = - 3 m = - 2