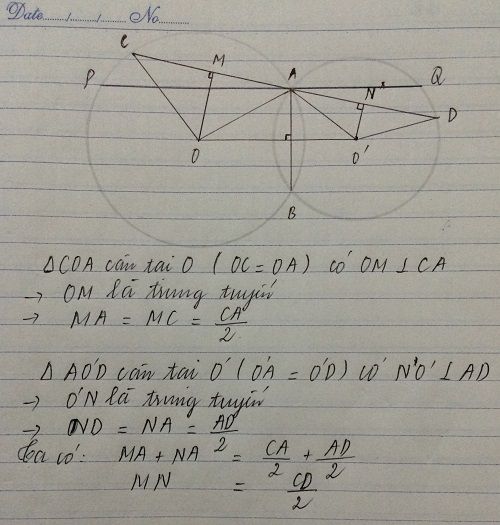Cho (O) và (O') cắt nhau ở A và B. Qua A kẻ 2 cát tuyến CD và EF ( C và E thuộc (O); D và F thuộc (O') ).Từ B kẻ BH vuông góc với CD, BK vuông góc với EF. biết góc BAC = góc BAF. Chứng minh tam giác BHC = tam giác BKE

Những câu hỏi liên quan
Cho 2 đường tròn (O) và (O') cắt nhau ở A và B (O và O' thuộc hai nửa mặt phẳng bờ AB).Qua A kẻ 2 cát tuyến CD và EF (C và E thuộc (O),D và F thuộc (O').Từ B kẻ BH vuông góc với CD,kẻ BK vuông góc với EF.Biết góc CAB bằng góc BAF. a.Chứng minh tam giác BHC bằng tam giác BKE b.So sánh CD và EF
Xem chi tiết
Cho (O) và (O) cắt nhau ở A và B (O và O thuộc 2 nửa mặt phẳng bờ AB), một cát tuyến kẻ qua A cắt (O) ở C và cắt (O) ở D. Kẻ OM vuông góc với CD, ON vuông góc CD.a) C/m MN 1/2CDb) Gọi I là trung điểm của MN. Cmr đường thẳng kẻ qua I vuông góc với Cd đi qua 1 điểm cố định khi cát tuyến CD kẻ qua A thay đổic) Qua A kẻ cát tuyến // với đường nối tâm OO cắt (O) ở P và cắt (O) ở Q. So sánh PQ và CD
Đọc tiếp
Cho (O) và (O') cắt nhau ở A và B (O và O' thuộc 2 nửa mặt phẳng bờ AB), một cát tuyến kẻ qua A cắt (O) ở C và cắt (O') ở D. Kẻ OM vuông góc với CD, O'N vuông góc CD.
a) C/m MN = 1/2CD
b) Gọi I là trung điểm của MN. Cmr đường thẳng kẻ qua I vuông góc với Cd đi qua 1 điểm cố định khi cát tuyến CD kẻ qua A thay đổi
c) Qua A kẻ cát tuyến // với đường nối tâm OO' cắt (O) ở P và cắt (O') ở Q. So sánh PQ và CD
cho 2 đường tròn (O) và (O') cắt nhau tại A và B . trên nửa mặt phẳng bờ OO' chứa B,vẽ tiếp tuyến chung EF(E thuộc (O),F thuộc (O')).Một cát tuyến qua A và song song với EF cắt (O) tại C và cắt (O') tại D.Hai đường thẳng CE , DF cắt nhau tại I CMR : IA vuông góc với CD
Cho đường tròn (O) và (O) cắt nhau tại A và B (O,O thuộc 2 nửa mặt phẳng bờ AB), một cát tuyến kẻ qua A cắt (O) ở C, cắt (O) ở D. Kẻ OM vuông góc với CD, ON vuông góc với CDa) Chứng minh: CD2MNb) Gọi I là trung điểm của MN. Chứng minh: đường thẳng kẻ qua I vuông góc với BC đi qua 1 điểm cố định khi cát tuyến vẽ qua A thay đổic) Qua A kẻ cát tuyến // với đường nối tâm OO, cắt (O) tại P, cắt (O) tại Q. So sánh PQ và CD.
Đọc tiếp
Cho đường tròn (O) và (O') cắt nhau tại A và B (O,O' thuộc 2 nửa mặt phẳng bờ AB), một cát tuyến kẻ qua A cắt (O) ở C, cắt (O') ở D. Kẻ OM vuông góc với CD, O'N vuông góc với CD
a) Chứng minh: CD=2MN
b) Gọi I là trung điểm của MN. Chứng minh: đường thẳng kẻ qua I vuông góc với BC đi qua 1 điểm cố định khi cát tuyến vẽ qua A thay đổi
c) Qua A kẻ cát tuyến // với đường nối tâm OO', cắt (O) tại P, cắt (O') tại Q. So sánh PQ và CD.
http://lazi.vn/edu/exercise/cho-o-va-o-cat-nhau-o-a-va-b-o-va-o-thuoc-2-nua-mat-phang-bo-ab-mot-cat-tuyen-ke-qua-a-cat-o-o-c-va-cat-o
Đúng 0
Bình luận (0)
Cho 2 đường tròn (O) và (O) cắt nhau ở A và B ( O và O thuộc hai nửa mặt phẳng bờ AB). Một cát tuyến kẻ qua A cắt đường tròn (O) ở C, cắt đường tròn (O) ở D. Kẻ OM vuông góc với CD và ON⊥ CDa) CMR: MN 1/2 CDb) Gọi I là trung điểm của MN. CMR đường thẳng kẻ qua I vuông góc với BC đi qua 1 điểm cố định khi cắt tuyến CD kẻ qua A thay đổic) Qua A kẻ cát tuyến song song với đường nối tâm OO cắt đường tròn (O) ở P, cắt đường tròn (O) ở Q. so sánh độ dài các đoạn PQ và CD
Đọc tiếp
Cho 2 đường tròn (O) và (O') cắt nhau ở A và B ( O và O' thuộc hai nửa mặt phẳng bờ AB). Một cát tuyến kẻ qua A cắt đường tròn (O) ở C, cắt đường tròn (O') ở D. Kẻ OM vuông góc với CD và O'N⊥ CD
a) CMR: MN = 1/2 CD
b) Gọi I là trung điểm của MN. CMR đường thẳng kẻ qua I vuông góc với BC đi qua 1 điểm cố định khi cắt tuyến CD kẻ qua A thay đổi
c) Qua A kẻ cát tuyến song song với đường nối tâm OO' cắt đường tròn (O) ở P, cắt đường tròn (O') ở Q. so sánh độ dài các đoạn PQ và CD
Cho 2 đường tròn (O) và (O) giao nhau ở A và B ( O và O thuộc 2 nửa mặt phẳng bờ AB ). Một cát tuyển kẻ qua A cắt đường tròn (O) ở C, cắt đường tròn (O) ở D. Kẻ OM vuông góc CD và ON vuông góc CD. a) CM MN1/2 CDb) Gọi I là trung điểm của MN. CMR đường thẳng kẻ qua I vuông góc với CD luôn luôn đi qua một điểm cố định khi cát tuyến CAD thay đổic) Qua A kẻ cát tuyến // với đường nối tâm OO cắt đường tròn (O) ở P, cắt đường tròn (O) ở Q. So sánh độ dài các đoạn CD và PQ
Đọc tiếp
Cho 2 đường tròn (O) và (O') giao nhau ở A và B ( O và O' thuộc 2 nửa mặt phẳng bờ AB ). Một cát tuyển kẻ qua A cắt đường tròn (O) ở C, cắt đường tròn (O') ở D. Kẻ OM vuông góc CD và O'N vuông góc CD.
a) CM MN=1/2 CD
b) Gọi I là trung điểm của MN. CMR đường thẳng kẻ qua I vuông góc với CD luôn luôn đi qua một điểm cố định khi cát tuyến CAD thay đổi
c) Qua A kẻ cát tuyến // với đường nối tâm OO' cắt đường tròn (O) ở P, cắt đường tròn (O') ở Q. So sánh độ dài các đoạn CD và PQ
Chắc câu a và câu b dễ rồi
cô chỉ em làm câu c.
Gọi L là trung điểm AP K là trung điểm AQ
=> PQ=2LK=2OO'
Mà CD=2MN , MN<OO,
=> CD<OO'<PQ
Đúng 0
Bình luận (0)
Bởi vì MN là hình chiếu của OO' lên CD
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Ai giúp mình bài này với: Cho (O) và (O) cắt nhau ở A và B (O và O khác phía), một cát tuyến kẻ qua A cắt (O) ở C và cắt (O) ở D. Kẻ OM vuông góc với CD, ON vuông góc CD.a) C/m MN 1/2CDb) Gọi I là trung điểm của MN. Cmr đường thẳng kẻ qua I vuông góc với CD đi qua 1 điểm cố định khi cát tuyến CD kẻ qua A thay đổic) Qua A kẻ cát tuyến song song với đường nối tâm OO cắt (O) ở P và cắt (O) ở Q. So sánh PQ và CD(Chỉ cần giúp ý c thui)Cảm ơn nhiều :)
Đọc tiếp
Ai giúp mình bài này với:
Cho (O) và (O') cắt nhau ở A và B (O và O' khác phía), một cát tuyến kẻ qua A cắt (O) ở C và cắt (O') ở D. Kẻ OM vuông góc với CD, O'N vuông góc CD.
a) C/m MN = 1/2CD
b) Gọi I là trung điểm của MN. Cmr đường thẳng kẻ qua I vuông góc với CD đi qua 1 điểm cố định khi cát tuyến CD kẻ qua A thay đổi
c) Qua A kẻ cát tuyến song song với đường nối tâm OO' cắt (O) ở P và cắt (O') ở Q. So sánh PQ và CD
(Chỉ cần giúp ý c thui)
Cảm ơn nhiều :)
mọi người giupa hộ mình bài này với mình đang cần gấp : cho (o) và (o') cắt nhau tại A và B , qua A vẽ 2 cát tuyến CD và È với C,E thuộc (o), D,F thuộc (o'), cho góc EAB= góc DAB. chứng minh rằng CD=EF.
Cho hai đường tròn (O) và (O') ở ngoài nhau. Kẻ các tiếp tuyến chung ngoài AB và CD (Ạ và C thuộc (O), B và D thuộc (O')). Tiếp tuyến chung trong MN cắt AB và CD theo thứ tự là E và F (M thuộc (O), N thuộc (O')). Chứng minh:
a, AB = EF
b, EM = FN
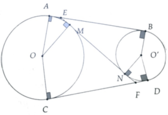
a, Ta có AB = AE + BE = EM + EN
Và CD = FD + FC = NF + NE
=> AB + CD = 2EF => AB = EF
b, Ta có EM = AB – EB = EF – EN = NF
Đúng 1
Bình luận (0)
Cho 2 đường tròn (O) và (O') cắt nhau tại A và B. Kẻ tiếp tuyến chung CD (C, D là tiếp điểm, C thuộc (O), D thuộc (O')). Đường thẳng qua A song song với CD cắt (O) tại E, (O') tại F. Gọi M, N theo thứ tự là giao điểm BD và BC với EF. Gọi I là giao điểm của EC với FD. CMR:
a) CMR tứ giác BCID nội tiếp.
b) CD là trung trực của đoạn thẳng Al.
c) IA là phân giác góc MIN.
a: TH1: A và CD nằm cùng một phía so với đường O'O
góc ABC=góc AEC=góc ICD
góc DBC=gsoc AED=góc IDC
=>góc DBA+góc DIC=góc ABC+góc DBC+góc DIC
=góc ICD+góc IDC+góc DIC=180 độ
=>BCID nội tiếp
TH2: A và CD nằm khác phía so với O'O
ABCE nội tiếp (O)
=>góc BCE+góc BAE=180 độ
=>góc BCE=góc BAF
Tương tự, ta được: góc BAF=góc BDI
=>góc BCE=góc BDI
=>góc BCI+góc BDI=180 độ
=>BCID nội tiếp
b: góc ICD=góc CEA=góc DCA
=>góc ICD=góc DCA
Chứng minh tương tự, ta được: góc IDC=góc CDA
Xét ΔICD và ΔACD có
góc ICD=góc DCA
CD chung
góc IDC=góc CDA
=>ΔICD=ΔACD
=>DI=DA và CI=CA
=>CD là trung trực của AI
c:
CD vuông góc AI
=>AI vuông góc MN
Gọi K là giao của AB và CD
Chứng minh được CK^2=KA*KB=KD^2
=>KC=KC
CD//MN
=>KC/AN=KD/AM=KB/AB
=>AN=AM
=>ΔIMN cân tại I
=>IA là phân giác của góc MIN
Đúng 0
Bình luận (0)