a, Ta có AB = AE + BE = EM + EN
Và CD = FD + FC = NF + NE
=> AB + CD = 2EF => AB = EF
b, Ta có EM = AB – EB = EF – EN = NF
Đúng 1
Bình luận (0)
Các câu hỏi tương tự
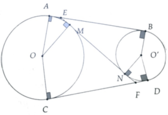
Cho 2 đường tròn O và O' ngoài nhau. Kẻ các tiếp tuyến chung ngoài AB, CD (A,C thuộc đường tròn O; B,D thuộc đường tròn O'). TIếp tuyến chung trong MN cắt AB và CD theo E và F (M thuộc O, N thuộc O')
a. AB=EF
b. EM=FN
Cho hai đường tròn (O) và (O) ở ngoài nhau. Kẻ các tiếp tuyến chung ngoài AB và AB, các tiếp tuyến chung CD và EF (A, A, C, E thuộc (O); B, B, D, F thuộc (O)). Gọi M là giao điểm của AB và EF, N là giao điểm của AB và CD, H là giao điểm của MN và OO. Chứng minh rằng:a) MN vuông góc với OO;b) Năm điểm O, B, M, H, F thuộc cùng một đường tròn;c) Năm điểm O, A, M, E, H thuộc cùng một đường tròn;d) Ba điểm H, D, B thẳng hàng;e) Ba điểm A, H, C thẳng hàng.
Đọc tiếp
Cho hai đường tròn (O) và (O') ở ngoài nhau. Kẻ các tiếp tuyến chung ngoài AB và A'B', các tiếp tuyến chung CD và EF (A, A', C, E thuộc (O); B, B', D, F thuộc (O')). Gọi M là giao điểm của AB và EF, N là giao điểm của A'B' và CD, H là giao điểm của MN và OO'. Chứng minh rằng:
a) MN vuông góc với OO';
b) Năm điểm O', B, M, H, F thuộc cùng một đường tròn;
c) Năm điểm O, A, M, E, H thuộc cùng một đường tròn;
d) Ba điểm H, D, B thẳng hàng;
e) Ba điểm A, H, C thẳng hàng.
Cho hai đường tròn (O) và (O) ở ngoài nhau. Kẻ các tiếp tuyến chung ngoài AB và AB, các tiếp tuyến chung CD và EF (A, A, C, E thuộc (O); B, B, D, F thuộc (O)). Gọi M là giao điểm của AB và EF, N là giao điểm của AB và CD, H là giao điểm của MN và OO. Chứng minh rằng:a) MN vuông góc với OO;b) Năm điểm O, B, M, H, F thuộc cùng một đường tròn;c) Năm điểm O, A, M, E, H thuộc cùng một đường tròn;d) Ba điểm H, D, B thẳng hàng;e) Ba điểm A, H, C thẳng hàng.
Đọc tiếp
Cho hai đường tròn (O) và (O') ở ngoài nhau. Kẻ các tiếp tuyến chung ngoài AB và A'B', các tiếp tuyến chung CD và EF (A, A', C, E thuộc (O); B, B', D, F thuộc (O')). Gọi M là giao điểm của AB và EF, N là giao điểm của A'B' và CD, H là giao điểm của MN và OO'. Chứng minh rằng:
a) MN vuông góc với OO';
b) Năm điểm O', B, M, H, F thuộc cùng một đường tròn;
c) Năm điểm O, A, M, E, H thuộc cùng một đường tròn;
d) Ba điểm H, D, B thẳng hàng;
e) Ba điểm A, H, C thẳng hàng.
Cho 2 đường tròn (O) và (O') ở ngoài nhau. Gọi AB và CD là các tiếp tuyến chung ngoài trong đó A, C thuộc (O); B, D thuộc (O'). Đường thẳng AD cắt (O) và (O') tại E và F. Chứng minh: a) A, B, C, D cùng thuộc 1 đường tròn. b) AE=DF
Cho 2 đường tròn (O) và (O') ở ngoài nhau. Gọi AB và CD là các tiếp tuyến chung ngoài trong đó A, C thuộc (O); B, D thuộc (O'). Đường thẳng AD cắt (O) và (O') tại E và F. Chứng minh: a) A, B, C, D cùng thuộc 1 đường tròn. b) AE=DF
Cho hai đường tròn (O) và (O') ngoài nhau, tiếp tuyến chung trong CD và tiếp tuyến chung ngoài AB ( A , C thuộc (O), B , D thuộc (O')). Chứng minh rằng AC , BD và OO' đồng quy
Cho hai đường tròn (O; 6 cm) và (O'; 2 cm) nằm ngoài nhau. Gọi AB là tiếp tuyến chung ngoài, CD là tiếp tuyến chung trong CD của hai đường tròn (A và C thuộc (O); B và D thuộc (O’)). Biết AB = 2CD, tính độ dài đoạn nối tâm OO'
Cho đường tròn (O) và (O1 ) ở ngoài nhau, tiếp tuyến chung ngoài AB ( A thuộc O, B thuộc O1 ). Tiếp tuyến chung trong CD và EF ( C, E thuộc O; D, F thuộc O1 ). CD cắt AB tại M, EF cắt AB tại N
a) CM: AM = BN
b) CM: góc OMO1 = góc ONO1
c) CM: AO. BO1 = AM. BM
Cho 2 đường tròn (O)và (O') ở ngoài nhau. Kẻ tiếp tuyến chung ngoài AB và tiếp tuyến chung trong EF ( A,E thuộc đường tròn(O); B,F thuộc đường tròn (O')). M là giao điểm của AB và EF. Chứng minh:
a, Tam giác AOM đồng dạng với tam giác BMO'
b, AE vuông góc với BF
c, Gọi N llaf giao điểm của AE và BF. Chứng minh: 3 điểm O,N,O' thẳng hàng