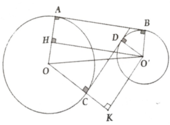
Kẻ O’H ⊥ OA; O’K ⊥ OC
OH = 4; OK = 8
Đặt CD = x => AB = 2x
O O ' 2 = 64 + x 2
và O O ' 2 = 16 + 4 x 2
=> x = 4 => OO' = 80 cm

Kẻ O’H ⊥ OA; O’K ⊥ OC
OH = 4; OK = 8
Đặt CD = x => AB = 2x
O O ' 2 = 64 + x 2
và O O ' 2 = 16 + 4 x 2
=> x = 4 => OO' = 80 cm
Cho hai đường tròn (O; R) và (O'; r) ở ngoài nhau. Gọi MN là tiếp tuyến chung ngoài, EF là tiếp tuyến chung trong (M và E thuộc (O), N và F thuộc (O')). Tính bán kính của đường tròn (O) và (O') trong các trường họp sau:
a, OO' = 10 cm, MN = 8cm và EF = 6 cm
b, OO' = 13 cm, MN = 12 cm và EF = 5 cm
Cho hai đường tròn (O) và (O') ngoài nhau, tiếp tuyến chung trong CD và tiếp tuyến chung ngoài AB ( A , C thuộc (O), B , D thuộc (O')). Chứng minh rằng AC , BD và OO' đồng quy
1, Cho 2 đường tròn đồng tâm O. Gọi AB là dây bất kì của đường tròn nhỏ. Đường thẳng AB cắt đường tròn lớn ở C và D ( A nằm giữa B và C ). So sánh các độ dài AC và BD.
2. Cho 2 đường tròn (O) và (O') tiếp xúc ngoài tại A. Gọi CD là tiếp tuyến chung ngoài của 2 đường tròn (C thuộc (O), D thuộc (O')).
a, Tính số đo góc CAD
b, Tính độ dài CD biết OA =4,5cm,O'A=2cm
Cho 2 đường tròn ( O ) và ( O' ) tiếp xúc ngoài tại A . Gọi CD là tiếp tuyến chung ngoài của 2 đường tròn ( với C thuộc ( O ) ) và ( N , NE)
a, Tính số đo góc CAD
b,Tính độ dài CD biết OA=4,5cm , O'A = 2 cm
Cho hai đường tròn (O) và (O') ở ngoài nhau. Kẻ các tiếp tuyến chung ngoài AB và CD (Ạ và C thuộc (O), B và D thuộc (O')). Tiếp tuyến chung trong MN cắt AB và CD theo thứ tự là E và F (M thuộc (O), N thuộc (O')). Chứng minh:
a, AB = EF
b, EM = FN
cho đường tròn (O;4,5 cm) và đường tròn (O';2 cm) tiếp xúc ngoài tại A.Gọi CD là tiếp tuyến chung ngoài (C thuộc đtròn tâm O, D thuộc đtròn tâm O'). Tiếp tuyến chung trong của 2 đtròn cắt CD tại M.
a. TÍnh số đo góc OMO' và góc CAD
b. Tính độ dài CD
c. Chứng tỏ đường tròn tâm I dường kính OO' tiếp xúc với CD tại M.
và các bãn vẽ hình giùm mình luôn nha mình ko bít vẽ nên ko làm dc, cám ơn các bạn, bài này trong đề cương học kì mai cô giáo kiểm rồi các bạn giúp mình nha
Cho 2 đường tròn O và O' ngoài nhau. Kẻ các tiếp tuyến chung ngoài AB, CD (A,C thuộc đường tròn O; B,D thuộc đường tròn O'). TIếp tuyến chung trong MN cắt AB và CD theo E và F (M thuộc O, N thuộc O')
a. AB=EF
b. EM=FN
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Gọi CD là tiếp tuyến chung ngoài của hai đường tròn (C ∈ (O), D ∈ (O’)). Tính độ dài CD biết OA = 4,5cm, O’A = 2cm
Cho hai đường tròn (O) và (O') ở ngoài nhau. Kẻ các tiếp tuyến chung ngoài AB và A'B', các tiếp tuyến chung CD và EF (A, A', C, E thuộc (O); B, B', D, F thuộc (O')). Gọi M là giao điểm của AB và EF, N là giao điểm của A'B' và CD, H là giao điểm của MN và OO'. Chứng minh rằng:
a) MN vuông góc với OO';
b) Năm điểm O', B, M, H, F thuộc cùng một đường tròn;
c) Năm điểm O, A, M, E, H thuộc cùng một đường tròn;
d) Ba điểm H, D, B thẳng hàng;
e) Ba điểm A, H, C thẳng hàng.