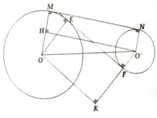
a, Kẻ O'H ⊥ OM; OK ⊥ O'F
có OH = R – r; O’K = R + r
Mà O H 2 = O O ' 2 - M N 2 = 36
O ' K 2 = O O ' 2 - E F 2 = 64
=> OH = 6 và O'K = 8
=> R = 7cm và r = 1cm
b, R = 17 2 cm và r = 7 2 cm
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho hai đường tròn (O) và (O) ở ngoài nhau. Kẻ các tiếp tuyến chung ngoài AB và AB, các tiếp tuyến chung CD và EF (A, A, C, E thuộc (O); B, B, D, F thuộc (O)). Gọi M là giao điểm của AB và EF, N là giao điểm của AB và CD, H là giao điểm của MN và OO. Chứng minh rằng:a) MN vuông góc với OO;b) Năm điểm O, B, M, H, F thuộc cùng một đường tròn;c) Năm điểm O, A, M, E, H thuộc cùng một đường tròn;d) Ba điểm H, D, B thẳng hàng;e) Ba điểm A, H, C thẳng hàng.
Đọc tiếp
Cho hai đường tròn (O) và (O') ở ngoài nhau. Kẻ các tiếp tuyến chung ngoài AB và A'B', các tiếp tuyến chung CD và EF (A, A', C, E thuộc (O); B, B', D, F thuộc (O')). Gọi M là giao điểm của AB và EF, N là giao điểm của A'B' và CD, H là giao điểm của MN và OO'. Chứng minh rằng:
a) MN vuông góc với OO';
b) Năm điểm O', B, M, H, F thuộc cùng một đường tròn;
c) Năm điểm O, A, M, E, H thuộc cùng một đường tròn;
d) Ba điểm H, D, B thẳng hàng;
e) Ba điểm A, H, C thẳng hàng.
Cho hai đường tròn (O) và (O) ở ngoài nhau. Kẻ các tiếp tuyến chung ngoài AB và AB, các tiếp tuyến chung CD và EF (A, A, C, E thuộc (O); B, B, D, F thuộc (O)). Gọi M là giao điểm của AB và EF, N là giao điểm của AB và CD, H là giao điểm của MN và OO. Chứng minh rằng:a) MN vuông góc với OO;b) Năm điểm O, B, M, H, F thuộc cùng một đường tròn;c) Năm điểm O, A, M, E, H thuộc cùng một đường tròn;d) Ba điểm H, D, B thẳng hàng;e) Ba điểm A, H, C thẳng hàng.
Đọc tiếp
Cho hai đường tròn (O) và (O') ở ngoài nhau. Kẻ các tiếp tuyến chung ngoài AB và A'B', các tiếp tuyến chung CD và EF (A, A', C, E thuộc (O); B, B', D, F thuộc (O')). Gọi M là giao điểm của AB và EF, N là giao điểm của A'B' và CD, H là giao điểm của MN và OO'. Chứng minh rằng:
a) MN vuông góc với OO';
b) Năm điểm O', B, M, H, F thuộc cùng một đường tròn;
c) Năm điểm O, A, M, E, H thuộc cùng một đường tròn;
d) Ba điểm H, D, B thẳng hàng;
e) Ba điểm A, H, C thẳng hàng.
Cho hai đường tròn (O; 6 cm) và (O'; 2 cm) nằm ngoài nhau. Gọi AB là tiếp tuyến chung ngoài, CD là tiếp tuyến chung trong CD của hai đường tròn (A và C thuộc (O); B và D thuộc (O’)). Biết AB = 2CD, tính độ dài đoạn nối tâm OO'
Cho hai đường tròn (O) và (O') ở ngoài nhau. Kẻ các tiếp tuyến chung ngoài AB và CD (Ạ và C thuộc (O), B và D thuộc (O')). Tiếp tuyến chung trong MN cắt AB và CD theo thứ tự là E và F (M thuộc (O), N thuộc (O')). Chứng minh:
a, AB = EF
b, EM = FN
cho (O) và (O') tiếp xúc ngoài tại A. Vẽ Tiếp tuyến chung ngoài MN với M thuộc (O), N thuộc (O') và tiếp tuyến chung trong cắt MN tại I chứng MInh MN là tiếp tuyến của đường tròn đường kính OO'
Cho 2 đường tròn O và O' ngoài nhau. Kẻ các tiếp tuyến chung ngoài AB, CD (A,C thuộc đường tròn O; B,D thuộc đường tròn O'). TIếp tuyến chung trong MN cắt AB và CD theo E và F (M thuộc O, N thuộc O')
a. AB=EF
b. EM=FN
Cho 2 đường tròn (O;R) và (OR) với RR. Hai tiếp tuyến chung ngoài MN và PQ ( M, P ∈(O) ; N, Q ∈(O) )a) CMR các đường thẳng MN, PQ, OO đồng quy.b) CM tứ giác MNQP là hình thanh cân.c) Xác định vị trí tương đối của đường tròn (O) và (O) sao cho đường tròn đường kính OO tiếp xú với đường thẳng MN.Giúp mình với ạ, mình cảm ơn rất nhiều ạ! (Làm theo cách làm lớp 9 giúp mình ạ)
Đọc tiếp
Cho 2 đường tròn (O;R) và (O'R') với R>R'. Hai tiếp tuyến chung ngoài MN và PQ ( M, P ∈(O) ; N, Q ∈(O') )
a) CMR các đường thẳng MN, PQ, OO' đồng quy.
b) CM tứ giác MNQP là hình thanh cân.
c) Xác định vị trí tương đối của đường tròn (O) và (O') sao cho đường tròn đường kính OO' tiếp xú với đường thẳng MN.
Giúp mình với ạ, mình cảm ơn rất nhiều ạ! (Làm theo cách làm lớp 9 giúp mình ạ)
Cho hai đường tròn ( O ) và ( O ) tiếp xúc ngoài ở A . Tiếp tuyến chung ngoài của 2 đường tròn , tiếp xúc với ( O ) ở M , tiếp xúc với đường tròn ( O ) ở N . Qua A kẻ đường thẳng vuông góc với OO cắt MN ở I . a) CM : tam giác AMN vuông b) Tam giác IOO là tam giác gì ? Vì sao c) CMR : đường thẳng MN tiếp xúc với đường tròn đường kính OO d) Cho biết OA 8cm , OA 4,5 cm . TÍnh độ dài MN .
Đọc tiếp
Cho hai đường tròn ( O ) và ( O' ) tiếp xúc ngoài ở A . Tiếp tuyến chung ngoài của 2 đường tròn , tiếp xúc với ( O ) ở M , tiếp xúc với đường tròn ( O' ) ở N . Qua A kẻ đường thẳng vuông góc với OO' cắt MN ở I .
a) CM : tam giác AMN vuông
b) Tam giác IOO' là tam giác gì ? Vì sao
c) CMR : đường thẳng MN tiếp xúc với đường tròn đường kính OO'
d) Cho biết OA = 8cm , OA' = 4,5 cm . TÍnh độ dài MN .
Cho 2 đường tròn O và O(1) ở ngoài nhau. Đường nối tâm OO(1) cắt đường tròn taamO và đường tròn tâm O(1) tại các điểm A B C D theo thứ tự trên đường thẳng. Kẻ tiếp tuyến chung ngoài EF ( E thuộc dt tâm O, F thuộc dt tâm O(1). Gọi M là giao điểm của AE và DM, N là giao điểm của EB và FC. Chứng minh rằng:
- Tứ giác MENF là hình chữ nhật
- MN vuông góc với AD
- ME.MA=MF.MD