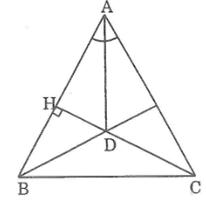
Vì ΔABC cân tại A nên đường phân giác của góc ở đỉnh A cũng là đường cao từ A.

Suy ra: AD ⊥ BC

Ta có: CH ⊥ AB (gt)

Tam giác ABC có hai đường cao AD và CH cắt nhau tại D nên D là trực tâm của ∆ABC

Suy ra BD là đường cao xuất phát từ đỉnh B đến cạnh AC.

Vậy BD ⊥ AC.

Tham khảo

ĐÂY LÀ KÍ HIỆU GÓC NHA (^)

Vì 3 tam giác này có 3 góc bằng nhau :

⇒BACˆ×3=180⇒BAC^×3=180 độ

⇒BACˆ=60⇒BAC^=60 độ

⇒ABDˆ=30⇒ABD^=30 độ

⇒ABDˆ+BADˆ⇒ABD^+BAD^ = 90 độ

⇒ΔBAD⇒ΔBAD ⊥ D

⇒BD⇒BD ⊥⊥ ACAC

Vì CE là tia phân giác của BCAˆBCA^

⇒ECAˆ⇒ECA^ =30=30 độ

⇒EACˆ+ECAˆ=90⇒EAC^+ECA^=90 độ

⇒ΔAEC⊥E⇒ΔAEC⊥E

⇒EC⊥AB

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có

góc A chung

=>ΔADB đồng dạng với ΔAEC

b: góc BEC=góc BDC=90 độ

=>BEDC nội tiếp

=>góc ADE=góc ABC

a: Xét ΔABD vuông tại D và ΔACE vuông tại E có

góc BAD chung

=>ΔABD đồng dạng với ΔACE

b: ΔABD đồng dạng với ΔACE

=>AD/AE=AB/AC

=>AD/AB=AE/AC

=>ΔADE đồng dạng với ΔABC

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có

BD=CE

góc ABD=góc ACE

=>ΔADB=ΔAEC

=>AB=AC

=>ΔABC cân tại A

b: ΔABC cân tại A

mà AD là đường phân giác

nên AD vuông góc BC

Xét ΔABC có

AD,CH là đường cao

AD cắt CH tại D

=>D là trực tâm

=>BD vuông góc AC

a,Vì tam giác ABC đều => BD,CE vừa là tia phân giác vừa là đường cao=>BD vuông góc AC và CE vuông góc AB 

b, vì hai tia phân giác BD và CE cắt nhau tại O suy ra O là tâm tam giác ABC suy ra OA = OB = OC (tính chất)

c, ta có góc AOB + góc BOC + góc COA = 360 độ mà  AOB = BOC= COA Suy ra 3 AOB= 360 suy ra AOB = 120 vậy AOB=BOC=COA=120 

Ta có hình vẽ sau:

a) Vì AB = BC = AC (gt)

=> ΔABC đều.

=> \(\widehat{A}=\widehat{B}=\widehat{C}=60^o\)

Có: \(\widehat{ABD}\) = \(\widehat{CBD}\) = \(\frac{60^o}{2}\) = 30^o

Trong ΔABD có:

\(\widehat{A}+\widehat{ABD}+\widehat{ADB}\) = 180^o

hay 60^o + 30^o + \(\widehat{ADB}\) = 180^o

=> \(\widehat{ADB}\) = 180^o - 60^o - 30^o = 90^o

Vì \(\widehat{ADB}\) = 90^o

=> BD \(\perp\) AC (đpcm)

b) Cm tương tự ta có:

\(\widehat{A}+\widehat{ACO}+\widehat{AOC}\) = 180^o

hay 60^o + 30^o + \(\widehat{AOC}\) = 180^o

=> \(\widehat{AOC}\) = 180^o - 60^o - 30^o = 90^o

Vì \(\widehat{AOC}=90^o\)

=> CE \(\perp\) AB

Mình nghĩ cái hình của bạn như này :)

\(\Delta ABC\) là tam giác cân <=> \(\widehat{BAC}=\widehat{ABC}=\widehat{ACB}=60^o\)

a)BD là tia phân giác của \(\widehat{ABC}\) => \(\widehat{ABD}=\widehat{DBC}=\frac{1}{2}.\widehat{ABC}=\frac{1}{2}.60^o=30^o\)

\(\Delta BDC\) có: \(\widehat{DBC}+\widehat{BDC}+\widehat{BCD}=180^o\) (tổng 3 góc trong 1 tam giác)

=>\(30^o+\widehat{BDC}+60^o=180^o\Rightarrow\widehat{BDC}=180^o-60^o-30^o=90^o\)

=>Góc BDC là góc vuông => \(BD\perp AC\) (đpcm)

b)CE là tia phân giác của góc ACB => \(\widehat{ACE}=\widehat{ECB}=\frac{1}{2}.\widehat{ACB}=\frac{1}{2}.60^o=30^o\)

\(\Delta EBC\) có: \(\widehat{ECB}+\widehat{BEC}+\widehat{EBC}1=180^o\) (tổng 3 góc trong 1 tam giác)

=>\(30^o+\widehat{BEC}+60^o=180^o\Rightarrow\widehat{BEC}=180^o-60^o-30^o=90^o\)

=>Góc BEC là góc vuông => \(CE\perp AB\) (đpcm)

c) Câu này có vấn đề nhé bạn, mình tính ra góc ACB=60^o, nhưng góc BOC=120^o cơ :v