Cho tam giác ABC cân tại A, đường caoAH. Biết góc A=48°;AH=13cm . Tính chu vi tam giác ABC

Những câu hỏi liên quan
CHo tam giác ABC vuông tại A, đường caoAH. Kẻ HD vuông góc AB tại D, HE vuông góc AC tại E. Biết AB=6cm, AC=8cm. TÍnh chu vi, diện tích tam giác ADE
Cho tam giác ABC vuông tại A, đường caoAH, biết BH =4cm, HC= 9cm. Tính các tỉ số của hai góc B và C.
\(\sin\widehat{B}=\cos\widehat{C}=\dfrac{AH}{AB}=\dfrac{6}{2\sqrt{13}}=\dfrac{3\sqrt{13}}{13}\)
\(\cos\widehat{B}=\sin\widehat{C}=\dfrac{2\sqrt{13}}{13}\)
\(\tan\widehat{B}=\cot\widehat{C}=\dfrac{3}{2}\)
\(\tan\widehat{C}=\cot\widehat{B}=\dfrac{2}{3}\)
Đúng 1
Bình luận (0)
cho tam giác ABC cân tại A đường cao AH biết góc A=48 độ AH= 13 cm tính chu vi tam giác ABC
Vì tam giác ABC là tam giác cân nên góc B = góc C = (180 độ - 48 độ):2 = 66 độ
Ta có : \(AB=AC=\frac{AH}{sinB}=\frac{13}{sin66^o}\) (cm)
\(BC=2HB=2.\frac{AH}{tanB}=\frac{26}{tan66^o}\) (cm)
Suy ra chu vi tam giác ABC : \(AB+BC+AC=\frac{26}{sin66^o}+\frac{26}{tan66^o}\) (cm)
Đúng 0
Bình luận (0)
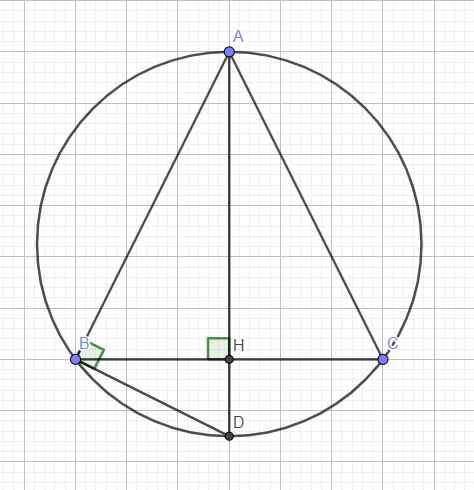
Cho tam giác ABC cân tại A nội tiếp đường tròn (O), cạnh bên bằng b, đường cao
AH=h. Tính bán kính đường tròn (O).
Kéo dài AH cắt đường tròn tại D \(\Rightarrow\) AD là đường kính
\(\Rightarrow\widehat{ABD}\) là góc nội tiếp chắn nửa đường tròn hay tam giác ABD vuông tại B
Áp dụng hệ thức lượng:
\(AB^2=AH.AD\Rightarrow AD=\dfrac{AB^2}{AH}=\dfrac{b^2}{h}\)
\(\Rightarrow2R=\dfrac{b^2}{h}\Rightarrow R=\dfrac{b^2}{2h}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A,đường caoAH biết AH=3m HN=4m tính BC
Cho tâm giác ABC cân tại A , đường caoAH . Vẽ HÈ vuông góc với AC, O là trung điểm của EH. CMR AO vuông góc với BE
Cho tam giác ABC cân tại A,đường trung tuyến BM,CN của tam giác ABC
a.C/m tứ giác BNMC là hình thang
b.C/m MN=1/2BC
c.Tính chu vi hình thang BNMC biết AB=5cm,đường caoAH=3cm
Giúp mình với chiều nay đi học rồi
a) BM,CN là trung tuyến=> M trung điểm AC, N trung điểm AB
=> MN là đường trung bình tam giác ABC=> MN//BC=> BNMC là hình thang.
b) MN là đường trung bình tam giác ABC => MN=1/2.BC
c) Vì tam giác ABC cân tại A nên AH cũng là trung tuyến=> H trung điểm BC=> BC=2BH
Định lí PYTAGO cho tam giác AHB vuông tại H
\(\Rightarrow AB^2=AH^2+HB^2\Rightarrow BH=\sqrt{AB^2-AH^2}=4cm\)
\(\Rightarrow BC=2BH=8cm\)
\(\Rightarrow MN=\frac{1}{2}BC=4cm\)
M trung điểm AC, N trung điểm AB \(\Rightarrow NB=MC=\frac{1}{2}AB=2,5cm\)
=> Chu vi BNMC=MN+NB+BC+CM=4+2,5+8+2,5=17cm
CORONA mà đi học à bạn ?!
mình ở tp vinh bạn ạ
Câu 1. Cho tam giác ABC vuông tại A, biết \(\dfrac{AB}{AC}=\dfrac{5}{6}\) đường cao
AH = 30cm. Tính HB, HC.
\(\dfrac{AB}{AC}=\dfrac{5}{6}\Rightarrow AC=\dfrac{6AB}{5}\) \(\Rightarrow AC^2=\dfrac{36AB^2}{25}\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Leftrightarrow\dfrac{1}{900}=\dfrac{1}{AB^2}+\dfrac{1}{\dfrac{36AB^2}{25}}\)
\(\Rightarrow AB^2=1525\Rightarrow AC^2=2196\)
\(BC^2=AB^2+AC^2=3721\Rightarrow BC=61\left(cm\right)\)
Áp dụng hệ thức lượng:
\(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=25\left(cm\right)\)
\(HC=BC-BH=36\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A,đường cao AH. Biết A=48°, AH=13cm.Tính chu vi tam giác ABC
Giúp với ,mơn nhiều !!
Vì tam giác ABC là tam giác cân nên góc B = góc C = ﴾180 độ ‐ 48 độ﴿:2 = 66 độ.
Ta có:\(AB=AC=\frac{AH}{sinB}=\frac{13}{sin66^o}\) ﴾cm﴿
\(BC=2HB=2.\frac{AH}{tanB}\frac{26}{tan66^o}\) ﴾cm﴿.
Suy ra chu vi tam giác ABC:
\(AB+BC+AC=\frac{26}{sin66^o}+\frac{26}{tan66^o}\) ﴾cm﴿
Đúng 0
Bình luận (0)