a) (d) đi qua điểm (1;2)

<=> 2 = k + 1 + k

<=> 1 = 2k

<=> k = 0,5

Vậy k = 0,5 thì (d) đi qua (1;2)

b) Để (d) // đgth y = 2x + 3

\(\Leftrightarrow\hept{\begin{cases}k+1=2\\k\ne3\end{cases}\Leftrightarrow\hept{\begin{cases}k=1\\k\ne3\end{cases}\Rightarrow}k=1}\)

Vậy k =1 thì (d) // đgth y = 2x +3

c) Gọi điểm cố định là (d) đi qua là (x₀;y₀)

Ta có y₀ = ( k +1) x₀ + k

<=> y₀ = kx₀ + x₀+k

<=> y₀ - x₀ - k ( x₀ + 1) = 0 \(\forall\)k

Để pt nghiệm đúng với mọi k <=> \(\hept{\begin{cases}x_0+1=0\\y_0-x_0=0\end{cases}\Leftrightarrow\hept{\begin{cases}x_0=-1\\y_0=-1\end{cases}}}\)

Điểm cố định (d) luôn đi qua là ( -1;-1)

a: Vì \(\left(d\right)\) đi qua \(A\left(1;2\right);B\left(-3;4\right)\) nên ta có hệ phương trình:

\(\left\{{}\begin{matrix}k+k'-3=2\\-3\left(k-3\right)+k'=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}k+k'=5\\-3k+k'=-5\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}4k=10\\k+k'=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}k=\dfrac{2}{5}\\k'=\dfrac{23}{5}\end{matrix}\right.\)

a: Thay x=0 và y=0 vào \(\left(d\right)\), ta được:

k=0

\(\left(d_1\right):y=-x+1\)

\(\left(d_2\right):y=x-1\)

\(\left(d_3\right):y=\dfrac{k+1}{1-k}x+\dfrac{k+1}{k-1}\)

a) Để (d1) và (d3) vuông góc với nhau:

\(\Leftrightarrow\left(-1\right)\left(\dfrac{k+1}{1-k}\right)=-1\)\(\Leftrightarrow k=0\)(thỏa)

Vậy k=0

b)Giao điểm của (d1) và (d2) là nghiệm của hệ \(\left\{{}\begin{matrix}y=-x+1\\y=x-1\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}y=0\\x=1\end{matrix}\right.\)

Để (d1);(d2);(d3) đồng quy\(\Leftrightarrow\) (d3) đi qua điểm (1;0)

\(\Rightarrow0=\dfrac{k+1}{1-k}.1+\dfrac{k+1}{k-1}\)\(\Leftrightarrow0=0\)(lđ)

Vậy với mọi k thì (d1);d2);(d3) luôn cắt nhau tại một điểm

c)Gỉa sử \(M\left(x_0;y_0\right)\) là điểm cố định mà (d3) luôn đi qua

Khi đó \(\left(k+1\right)x_0+\left(k-1\right)y_0=k+1\) luôn đúng với mọi k

\(\Leftrightarrow k\left(x_0+y_0-1\right)+x_0-y_0-1=0\) luôn đúng với mọi k

\(\Leftrightarrow\left\{{}\begin{matrix}x_0+y_0-1=0\\x_0-y_0-1=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x_0=2\\y_0=1\end{matrix}\right.\)

Vậy \(M\left(2;1\right)\) là điểm cố định mà (d3) luôn đi qua.

a. k = 0

b. k = 1 -\(\sqrt{2}\)

c . k = \(\sqrt{3}\)

Đk: \(k\ge0\)

a)

A(0,2\(\sqrt{3}\))

x=0

\(\Rightarrow y=\sqrt{k}+\sqrt{3}\)

\(\Rightarrow\sqrt{k}=2\sqrt{3}-\sqrt{3}=\sqrt{3}\)

\(\Rightarrow k=3\) nhận

b)

\(B\left(1;0\right)\)

\(\Leftrightarrow\dfrac{\sqrt{k}+1}{\sqrt{3}-1}.1+\sqrt{k}+\sqrt{3}=0\)

\(\Leftrightarrow\sqrt{k}+1+\sqrt{k}.\left(\sqrt{3}-1\right)+\sqrt{3}\left(\sqrt{3}-1\right)=0\)

\(\Leftrightarrow\sqrt{3}\sqrt{k}+4-\sqrt{3}=0\)

\(4>\sqrt{3}\Rightarrow Vo..N_0\)

(d) không đi qua điểm B(1;0)

c) Sửa đề \(k\ge0\)

\(\Leftrightarrow y=\dfrac{\sqrt{k}.x+x+\sqrt{3}\sqrt{k}-\sqrt{k}+\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}\)

\(\Leftrightarrow y=\dfrac{\sqrt{k}\left(x+\sqrt{3}-1\right)+x+\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}\)

Với \(x=1-\sqrt{3}\) => y=\(\dfrac{\left(\sqrt{3}-1\right)\left(\sqrt{3}-1\right)}{\sqrt{3}-1}=\sqrt{3}-1\) không phụ thuộc k

Điểm cố định

D\(\left(\left(1-\sqrt{3}\right);\left(\sqrt{3}+1\right)\right)\)

Gọi điểm cố định mà các đường thẳng (d) đều đi qua P( x o ,  y o ).

Ta có:

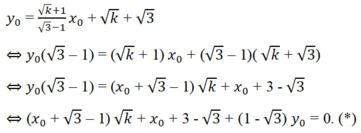
Phương trình (*) nghiệm đúng với mọi giá trị không âm của k , do đó ta có:

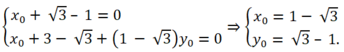
Vậy, với k ≥ 0, các đường thẳng (d) đều đi qua điểm cố định P(1-  3 ;  3  – 1).