tìm số nguyên m thuộc [-2018;2018] sao cho phương trình |x+1| +m|x-1|=3 luôn có một nghiệm duy nhất

Những câu hỏi liên quan
Cho hàm số
y
1
4
8
m
3
-
x
4
-
2
x
3
+
2
m
-
7
x
2
-
12
x
+
2018
với m là tham số. Tìm tất cả các số nguyên m thuộc đoạn
-
2018...
Đọc tiếp
Cho hàm số y = 1 4 8 m 3 - x 4 - 2 x 3 + 2 m - 7 x 2 - 12 x + 2018 với m là tham số. Tìm tất cả các số nguyên m thuộc đoạn - 2018 ; 2018 để hàm số đã cho đồng biến trên - 1 2 ; - 1 4 .
A. 2016.
B. 2019 .
C. 2020 .
D. 2015 .
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2018; 2018] để hàm số y = (m – 2)x + 2m đồng biến trên R.
A. 2015
B. 2017
C. Vô số
D. 2016
Hàm số bậc nhất đồng biến suy ra a > 0 hay m > 2
m thuộc đoạn [-2018; 2018] suy ra m thuộc {3; 4; ...; 2018}
Vậy có 2016 giá trị nguyên của m cần tìm.
Chọn D.
Đúng 0
Bình luận (0)
tìm số nguyên x để phân số A = 2023/x+5 với x không thuộc -5 có giá trị lớn nhất
A. -6
B. -4
C. -2022
D. 2018
tính tổng các số nguyên x bt
a) -2017≤ x ≤ 2018
b) a+3 ≤ x ≤ a+2018(a thuộc n)
a) \(-2017\le x\le2018\)
\(\Rightarrow x\in\left\{-2017;-2016;...0;1;2;...2018\right\}\)
\(\Rightarrow\left(-2017\right)+\left(-2016\right)+...+0+1+2;...+2018=2018\)
b) \(a+3\le x\le a+2018\) \(\left(a\in N\right)\)
\(\Rightarrow x\in\left\{a+3;a+4;...a+2018\right\}\)
\(\Rightarrow T=a+3+a+4+...+a+2018\)
\(\Rightarrow T=a+a+...+a+3+4+...2018\)
\(\Rightarrow T=2016a+2016=2016\left(a+1\right)\)
Đúng 0
Bình luận (0)
Tìm m; n thuộc N sao cho: 2^m + 20117 = /n - 2018/ + n - 2018
Gọi S là tập hợp các giá trị nguyên của tham số m để phương trình
2
log
2
x
4
+
2
log
2
x
8
-
2
m
+
2018
0
có ít nhất một nghiệm thuộc đoạn
1
;
2
. Số phần tử...
Đọc tiếp
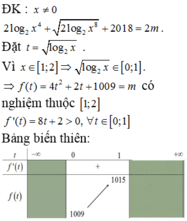
Gọi S là tập hợp các giá trị nguyên của tham số m để phương trình 2 log 2 x 4 + 2 log 2 x 8 - 2 m + 2018 = 0 có ít nhất một nghiệm thuộc đoạn 1 ; 2 . Số phần tử của S là
A. 7
B. 9
C. 8
D. 6
Gọi S là tập hợp các nghiệm thuộc đoạn
0
;
2
π
của phương trình
sin
2
x
+
3
cos
2
x
−
2
. Biết rằng tổng các phần tử thuộc S bằng
m
π
n
, trong đó m, n là các số nguyên dương và phân số
m...
Đọc tiếp
Gọi S là tập hợp các nghiệm thuộc đoạn 0 ; 2 π của phương trình sin 2 x + 3 cos 2 x = − 2 . Biết rằng tổng các phần tử thuộc S bằng m π n , trong đó m, n là các số nguyên dương và phân số m n tối giản. Tính T = 22 m + 6 n + 2018 .
A. T = 2322
B. T = 2340
C. T = 2278
D. T = 2388
Đáp án A.
Ta có
sin 2 x + 3 cos 2 x = − 2 ⇔ cos 2 x − π 6 = − 2 2 .
⇔ x = − 7 π 24 + k π hoặc x = 11 π 24 + k π , k ∈ ℤ .
Nghiệm thuộc đoạn 0 ; 2 π của phương trình là 11 π 24 ; 17 π 24 ; 35 π 24 ; 41 π 24 .
Suy ra S = 11 π 24 ; 17 π 24 ; 35 π 24 ; 41 π 24 .
Do đó tổng các phần tử thuộc S là
11 π 24 + 17 π 24 + 35 π 24 + 41 π 24 = 104 24 π + 13 3 π
Ta có m=13 và n=3 nên T=2322.
Đúng 0
Bình luận (0)
Gọi S là tập hợp các nghiệm thuộc đoạn
0
;
2
π
của phương trình
sin
2
x
+
3
cos
2
x
−
2
. Biết rằng tổng các phần tử thuộc S bằng
m
π
n
, trong đó m, n là các số nguyên dương và phân số
m...
Đọc tiếp
Gọi S là tập hợp các nghiệm thuộc đoạn 0 ; 2 π của phương trình sin 2 x + 3 cos 2 x = − 2 . Biết rằng tổng các phần tử thuộc S bằng m π n , trong đó m, n là các số nguyên dương và phân số m n tối giản. Tính T=22m+6n+2018.
A. T=2322
B. T=2340
C. T=2278
D. T=2388
với mỗi số nguyên dương n, ta kí hiệu d(n) là số các ước nguyên dương của n và s(n) là tổng tất cả các ước nguyên dương đó .Chẳng hạn d(2018) = 4 vì 2018 có và chỉ có 4 ước Nguyên Dương là 1;2;1009; 2018 và s (2018) = 1 + 2 + 1009 + 2018 = 3030 Tìm tất cả các số nguyên dương x sao cho s(x).d(x)= 96
Vào đây tham khảo nha ! : Câu hỏi của Phạm Chí Cường - Toán lớp 6 | Học trực tuyến
Đúng 0
Bình luận (0)
Với mỗi số nguyên dương n, ta kí hiệu d(n) là số các ước nguyên dương của n và s(n) là tổng tất cả các ước nguyên dương đó. Ví dụ, d(2018) = 4 vì 2018 có (và chỉ có) 4 ước nguyên dương là 1; 2; 1009; 2018 và s(2018) = 1 + 2 + 1009 + 2018 = 3030. Tìm tất cả các số nguyên dương x sao cho s(x) . d(x) = 96