Các câu hỏi tương tự
Gọi S là tập hợp các nghiệm thuộc đoạn
0
;
2
π
của phương trình
sin
2
x
+
3
cos
2
x
−
2
. Biết rằng tổng các phần tử thuộc S bằng
m
π
n
, trong đó m, n là các số nguyên dương và phân số
m...
Đọc tiếp
Gọi S là tập hợp các nghiệm thuộc đoạn 0 ; 2 π của phương trình sin 2 x + 3 cos 2 x = − 2 . Biết rằng tổng các phần tử thuộc S bằng m π n , trong đó m, n là các số nguyên dương và phân số m n tối giản. Tính T = 22 m + 6 n + 2018 .
A. T = 2322
B. T = 2340
C. T = 2278
D. T = 2388
Cho hàm số yf(x) liên tục trên R và có đồ thị như hình vẽ bên. Gọi S là tập hợp tất cả các số nguyên m để phương trình f(sinx)3sinx+m có nghiệm thuộc khoảng
0
;
π
Tổng các phần tử của S bằng A. -5 B. -8 C. -6 D. -10
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ bên. Gọi S là tập hợp tất cả các số nguyên m để phương trình f(sinx)=3sinx+m có nghiệm thuộc khoảng 0 ; π Tổng các phần tử của S bằng
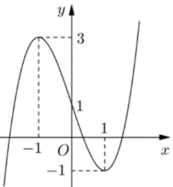
A. -5
B. -8
C. -6
D. -10
Cho hàm số
y
f
x
liên tục trên
ℝ
và có đồ thị như hình vẽ. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình
f
sin
x
3
sin
x
+
m
có nghiệm thuộc khoảng
0
;
π
. Tổng các phần tử của S bằng A. -10 B. -8 C. -...
Đọc tiếp
Cho hàm số y = f x liên tục trên ℝ và có đồ thị như hình vẽ. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình f sin x = 3 sin x + m có nghiệm thuộc khoảng 0 ; π . Tổng các phần tử của S bằng
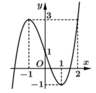
A. -10
B. -8
C. -6
D. -5
Gọi S là tập hợp các nghiệm thuộc đoạn
-
2
π
,
2
π
của phương trình
5
sin
x
+
cos
3
x
+
sin
3
x...
Đọc tiếp
Gọi S là tập hợp các nghiệm thuộc đoạn - 2 π , 2 π của phương trình
5 sin x + cos 3 x + sin 3 x 1 + 2 sin 2 x = cos 2 x + 3
Giả sử M,m là phần tử lớn nhất và nhỏ nhất của tập hợp S. Tính H=M-m.
A. H = 2 π
B. H = 10 π 3
C. H = 11 π 3
D. H = 7 π 3
Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho phương trình
2
sin
x
+
1
sin
x
+
2
m
có đúng hai nghiệm thuộc đoạn
0
;
π
. Khi đó S là A. một khoảng B. một đoạn C. một nửa khoảng D. một tập...
Đọc tiếp
Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho phương trình 2 sin x + 1 sin x + 2 = m có đúng hai nghiệm thuộc đoạn 0 ; π . Khi đó S là
A. một khoảng
B. một đoạn
C. một nửa khoảng
D. một tập hợp có hai phần tử
Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho phương trình
2
sin
x
+
1
sin
x
+
2
m có đúng hai nghiệm thuộc đoạn
0
;
π
. Khi đó S là A. một khoảng B. một đoạn C. một nửa khoảng D. một tập hợp có hai phần t...
Đọc tiếp
Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho phương trình 2 sin x + 1 sin x + 2 =m có đúng hai nghiệm thuộc đoạn 0 ; π . Khi đó S là
A. một khoảng
B. một đoạn
C. một nửa khoảng
D. một tập hợp có hai phần tử
Cho phương trình
2
-
m
3
-
3
m
2
+
1
.
log
81
x...
Đọc tiếp
Cho phương trình 2 - m 3 - 3 m 2 + 1 . log 81 x 3 - 3 x 2 + 1 + 2 + 2 - x 3 - 3 x 2 + 1 - 2 . log 3 1 m 3 - 3 m 2 + 1 + 2 = 0 . Gọi S là tập hợp tất cả các giá trị m nguyên để phương trình đã cho có số nghiệm thuộc đoạn 6 ; 8 . Tính tổng bình phương tất cả các phần tử của tập S.
A. 20
B. 28
C. 14
D. 10
Gọi S là tập hợp các số nguyên m để hàm số
y
f
(
x
)
x
+
2
m
-
3
x
-
3
m
+
2
đồng biến trên khoảng (-∞;-14) . Tính tổng T của các phần tử trong S A. T-10 B. T-9...
Đọc tiếp
Gọi S là tập hợp các số nguyên m để hàm số y = f ( x ) = x + 2 m - 3 x - 3 m + 2 đồng biến trên khoảng (-∞;-14) . Tính tổng T của các phần tử trong S
A. T=-10
B. T=-9
C. T=-6
D. T=-5
Biết rằng tập hợp tất cả các giá trị của tham số m để hàm số
f
x
x
2
+
2
x
+
2
m
−
1
x
−
m
đồng biến trên nửa khoảng
2
;...
Đọc tiếp
Biết rằng tập hợp tất cả các giá trị của tham số m để hàm số f x = x 2 + 2 x + 2 m − 1 x − m đồng biến trên nửa khoảng 2 ; + ∞ là S = − ∞ ; a b , trong đó a, b là các số nguyên dương và a b là phân số tối giản. Tính tổng bình phương của a và b.
A. 169
B. 41
C. 89
D. 81







