a) A ∪ B = (-∞; 15)

A ∩ B = [-2; 3)

b) Để A ⊂ B thì:

m - 1 > -2 và m + 4 ≤ 3

*) m - 1 > -2

m > -2 + 1

m > -1

*) m + 4 ≤ 3

m ≤ 3 - 4

m ≤ -1

Vậy không tìm được m thỏa mãn đề bài

a) A ∪ B = (-∞;15]

A∩B = [-2;3)

a) (-\(\infty\);15) ; [-2;3) 

b) -1<m≤-1

Ta thấy \(\left(2-2+1\right)\left(1-0+1\right)=2>0\Rightarrow A,B\) khác phía so với \(\Delta\)

Lấy B' đối xứng với B qua \(\Delta\)

BB' có phương trình \(2x+y+m=0\)

Do B thuộc đường thẳng BB' nên \(m=-2\Rightarrow BB':2x+y-2=0\)

B' có tọa độ là nghiệm của hệ \(\left\{{}\begin{matrix}x-2y+1=0\\2x+y-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{5}\\y=\dfrac{4}{5}\end{matrix}\right.\Rightarrow B'=\left(\dfrac{3}{5};\dfrac{4}{5}\right)\)

a, \(MA+MB=MA+MB'\ge AB'\)

\(min=AB'\Leftrightarrow M\) là giao điểm của AB' và \(\Delta\)

\(\Leftrightarrow...\)

b, \(\left|MA-MB\right|=\left|MA-MB'\right|\le AB'\)

\(max=AB'\Leftrightarrow M\) là giao điểm của AB' và \(\Delta\)

\(\Leftrightarrow...\)

a) Chọn \(t = 0;t = 1\) ta lần được được 2 điểm A và B thuộc đường thẳng \(\Delta \) là: \(A\left( {1; - 2} \right),B\left( { - 1; - 1} \right)\)

b) +) Thay tọa độ điểm C vào phương trình đường thẳng \(\Delta \) ta có: \(\left\{ \begin{array}{l}1 = 1 - 2t\\ - 1 =  - 2 + t\end{array} \right.\). Do hệ phương trình vô nghiệm nên C không thuộc đường thẳng \(\Delta \)

+) Thay tọa độ điểm D vào phương trình đường thẳng \(\Delta \) ta có: \(\left\{ \begin{array}{l}1 = 1 - 2t\\3 =  - 2 + t\end{array} \right.\). Do hệ phương trình vô nghiệm nên D không thuộc đường thẳng \(\Delta \)

Mặt phẳng (P) qua A và vuông góc d có phương trình:

\(2\left(x-1\right)+2\left(y+1\right)+1\left(z-1\right)=0\)

\(\Leftrightarrow2x+2y+z-1=0\)

Đường thẳng d' song song d và đi qua B (nên d' vuông góc (P)) có dạng:

\(\left\{{}\begin{matrix}x=4+2t\\y=2+2t\\z=-2+t\end{matrix}\right.\)

\(\Rightarrow\) Giao điểm C của d' và (P) thỏa mãn: 

\(2\left(4+2t\right)+2\left(2+2t\right)-2+t-1=0\Rightarrow t=-1\Rightarrow C\left(2;0;-3\right)\)

\(\Rightarrow\overrightarrow{AC}=\left(1;1;-4\right)\Rightarrow\) là 1 vtcp của \(\Delta\Rightarrow\) D là đáp án đúng

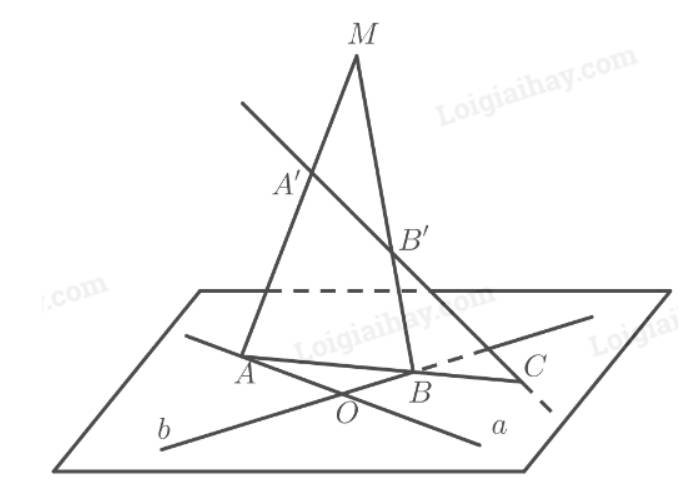
a) Ta có:

\(\begin{array}{l}\left. \begin{array}{l}M \in \left( {M,a} \right)\\M \in \left( {M,b} \right)\end{array} \right\} \Rightarrow M \in \left( {M,a} \right) \cap \left( {M,b} \right)\\\left. \begin{array}{l}O \in a \subset \left( {M,a} \right)\\O \in b \subset \left( {M,b} \right)\end{array} \right\} \Rightarrow O \in \left( {M,a} \right) \cap \left( {M,b} \right)\end{array}\)

Vậy giao tuyến của hai mặt phẳng \(\left( {M,a} \right)\) và \(\left( {M,b} \right)\) là đường thẳng \(MO\).

b) Ta có:

\(\begin{array}{l}\left. \begin{array}{l}A \in \left( {MAB} \right)\\A \in a \subset \left( {a,b} \right)\end{array} \right\} \Rightarrow A \in \left( {MAB} \right) \cap \left( {a,b} \right)\\\left. \begin{array}{l}B \in \left( {MAB} \right)\\B \in b \subset \left( {a,b} \right)\end{array} \right\} \Rightarrow B \in \left( {MAB} \right) \cap \left( {a,b} \right)\end{array}\)

Vậy giao tuyến của hai mặt phẳng \(\left( {MAB} \right)\) và \(\left( {a,b} \right)\) là đường thẳng \(AB\) (1).

c) Ta có:

\(\left. \begin{array}{l}A' \in MA \subset \left( {MAB} \right)\\B' \in MB \subset \left( {MAB} \right)\end{array} \right\} \Rightarrow A'B' \subset \left( {MAB} \right)\)

Vì \(C \in A'B' \subset \left( {MAB} \right)\) và \(C \in mp\left( {a,b} \right)\) nên điểm \(C\) nằm trên giao tuyến của hai mặt phẳng \(\left( {MAB} \right)\) và \(\left( {a,b} \right)\) (2).

Từ (1) và (2) suy ra ba điểm \(A,B,C\) thẳng hàng.

b: Để hai đường thẳng cắt nhau tại một điểm trên trục tung thì m-1=15

hay m=16

a) \(\overrightarrow {MN}  = 3\overrightarrow a \)có độ dài bằng 3 lần vectơ \(\overrightarrow a \), cùng hướng với vectơ \(\overrightarrow a \)

Suy ra, từ điểm M vẽ vectơ MN với độ dài là 6 ô vuông và có hướng từ trái sang phải

\(\overrightarrow {MP}  =  - 3\overrightarrow b \)có độ dài bằng 3 lần vectơ \( - \overrightarrow b \), ngược hướng với vectơ \(\overrightarrow b \)

Suy ra, từ điểm M vẽ vectơ MP với độ dài là 3 đường chéo ô vuông và có hướng từ trên xuống dưới chếch sang trái

b) Hình vuông với cạnh bằng 1 thì ta tính được đường chéo có độ dài là \(\sqrt 2 \); \(\left| {\overrightarrow b } \right| = \sqrt 2 \) . Suy ra:

\(\left| {3\overrightarrow b } \right| = 3\left| {\overrightarrow b } \right| = 3\sqrt 2 \); \(\left| { - 3\overrightarrow b } \right| = 3\left| {\overrightarrow { - b} } \right| = 3\sqrt 2 \); \(\left| {2\overrightarrow a  + 2\overrightarrow b } \right| = \left| {2\left( {\overrightarrow a  + \overrightarrow b } \right)} \right| = 2\left| {\overrightarrow a  + \overrightarrow b } \right|\)

Từ điểm cuối của vectơ \(\overrightarrow a \) vẽ một vectơ bằng vectơ \(\overrightarrow b \) ta có \(\overrightarrow c  = \overrightarrow a  + \overrightarrow b \)

Áp dụng định lý cosin ta tính được độ dài của vectơ \(\overrightarrow c \)là \(\left| {\overrightarrow c } \right| = \sqrt {{{\left| {\overrightarrow a } \right|}^2} + {{\left| {\overrightarrow b } \right|}^2} - 2\left| {\overrightarrow a } \right|\left| {\overrightarrow b } \right|\cos \left( {\widehat {\overrightarrow a ,\overrightarrow b }} \right)}  = \sqrt {{2^2} + {{\sqrt 2 }^2} - 2.2.\sqrt 2 .\cos \left( {135^\circ } \right)}  = \sqrt {10} \)

\( \Rightarrow \left| {2\overrightarrow a  + 2\overrightarrow b } \right| = 2\left| {\overrightarrow a  + \overrightarrow b } \right| = 2\left| {\overrightarrow c } \right| = 2\sqrt {10} \)

Ta có tọa độ vectơ \(\overrightarrow {OB} ,\overrightarrow {OA} \) chính là tọa độ điểm B và A

Nên ta có \(\overrightarrow {OB}  = \left( {{x_B};{y_B}} \right),\overrightarrow {OA}  = \left( {{x_A};{y_A}} \right)\)

\(\overrightarrow {AB}  = \overrightarrow {OB}  - \overrightarrow {OA}  = \left( {{x_B};{y_B}} \right) - \left( {{x_A};{y_A}} \right) = ({x_B} - {x_A};{y_B} - {y_A})\)