Cho tam giác ABC nội tiếp đường tròn tâm I(2;2), phân giác ngoài tại đỉnh A cắt BC tại D.đường tròn tâm I cắt AD tại điểm M,phương trình đường thẳng CM: x+y-2=0.Gọi J(-2;2) là tâm đường tròn ngoài tiếp tam giác ACD.Tìm tổng hoành độ các điểm ABC

Những câu hỏi liên quan
cho tam giác abc nội tiếp đường tròn (o), I là tâm đường tròn nội tiếp tam giác abc. AI cắt (o) tại M, c/m tam giác MIB cân
cho tam giác ABC nội tiếp trong đường tròn tâm O , BE và CF là hai đường cao , cắt nhau tại H , tứ giác AFHE nội tiếp trong đường tròn tâm I , BECF nội tiếp đường trfonf tâm M , chứng minh ME là tiếp tuyến của đương tròn tâm I
Xét tứ giác AFHE có
\(\widehat{AFH}+\widehat{AEH}=90^0+90^0=180^0\)
=>AFHE là tứ giác nội tiếp đường tròn đường kính AH
=>I là trung điểm của AH
=>IA=IH=IE=IF
Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}=90^0\)
=>BFEC là tứ giác nội tiếp đường tròn đường kính BC
=>M là trung điểm của BC
=>MB=MC=ME=MF
Gọi O là giao điểm của AH với BC
Xét ΔABC có
BE,CF là đường cao
BE cắt CF tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC tại O
ΔBHO vuông tại O
=>\(\widehat{OHB}+\widehat{OBH}=90^0\)
mà \(\widehat{OBH}+\widehat{OCE}=90^0\)(ΔBEC vuông tại E)
nên \(\widehat{OHB}=\widehat{OCE}\)
mà \(\widehat{OHB}=\widehat{IHE}\)(hai góc đối đỉnh)
nên \(\widehat{IHE}=\widehat{OCE}\)
IH=IE
=>\(\widehat{IHE}=\widehat{IEH}\)
mà \(\widehat{IHE}=\widehat{OCE}\)
nên \(\widehat{IEH}=\widehat{OCE}=\widehat{ECB}\)
ME=MB
=>ΔMEB cân tại M
=>\(\widehat{MEB}=\widehat{MBE}\)
=>\(\widehat{MEB}=\widehat{EBC}\)
\(\widehat{IEM}=\widehat{IEH}+\widehat{MEH}\)
\(=\widehat{EBC}+\widehat{ECB}\)
\(=90^0\)
=>ME là tiếp tuyến của (I)
Đúng 1
Bình luận (0)
Cho tam giác ABC, đường tròn (I) nội tiếp tam giác ABC tiếp xúc với AB,AC ở D,E. Gọi K là giao điểm của AI với (I). Cmr: K là tâm của đường tròn nội tiếp tam giác ADE.
Cho tam giác ABC , D là điểm trên cạnh BC sao cho đường tròn nội tiếp tam giác ABD và tam giác ADC tiếp xúc nhau tại một điểm thuộc cạnh AD. Gọi I, J lần lượt là tâm đường tròn nội tiếp tam giác ABD và tam giác ADC , O là tâm đường tròn ngoại tiếp tam giác AIJ
a) Xác định vị trí điểm D trên cạnh BC
b) Từ câu a) chứng minh rằng đường phân giác góc BAC qua tâm O
Cho tam giác ABC , D là điểm trên cạnh BC sao cho đường tròn nội tiếp tam giác ABD và tam giác ADC tiếp xúc nhau tại một điểm thuộc cạnh AD. Gọi I, J lần lượt là tâm đường tròn nội tiếp tam giác ABD và tam giác ADC , O là tâm đường tròn ngoại tiếp tam giác AIJ
a) Xác định vị trí điểm D trên cạnh BC
b) Từ câu a) chứng minh rằng đường phân giác góc BAC qua tâm O
Cho tam giác ABC nội tiếp đường tròn tâm O. Gọi I là tâm đường tròn nội tiếp tam giác ABC. AI cắt đường tâm O tại M. E là trung điểm của BC. ME cắt đường tròn tâm O tại N. Chứng minh góc BEI = góc ANI
Cho tam giác ABC nội tiếp đường tròn (O). P di chuyển trên cung
B
C
⏜
chứa A của (O). I là tâm đường tròn nội tiếp tam giác ABC. Q là tâm đường tròn nội tiếp tam giác PBC.1). Chứng minh rằng B, I, Q, C cùng nằm trên một đường tròn.2) Trên tia BQ, CQ lần lượt lấy các điểm M, N sao cho
B
M
B
I
,
C
N
C
I
. Chứng m...
Đọc tiếp
Cho tam giác ABC nội tiếp đường tròn (O). P di chuyển trên cung B C ⏜ chứa A của (O).
I là tâm đường tròn nội tiếp tam giác ABC. Q là tâm đường tròn nội tiếp tam giác PBC.
1). Chứng minh rằng B, I, Q, C cùng nằm trên một đường tròn.
2) Trên tia BQ, CQ lần lượt lấy các điểm M, N sao cho B M = B I , C N = C I . Chứng minh rằng MN luôn đi qua một điểm cố định.
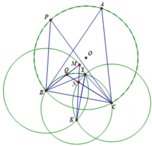
1) Ta có
B I C ^ = 180 0 − I B C ^ − I C B ^ = 180 0 − A B C ^ 2 − A C B ^ 2 = 180 0 − 180 ∘ − B A C ^ 2 = 90 0 + B A C ^ 2 ⇔ B A C ^ = 2 B I C ^ − 180 °
Tương tự B Q C ^ = 90 0 + B P C ^ 2 ⇔ B P C ^ = 2 B Q C ^ − 180 ° .
Tứ giác BPAC nội tiếp, suy ra B A C ^ = B P C ^ ⇒ B Q C ^ = B I C ^ , nên 4 điểm B, I, Q, C thuộc một đường tròn.
2) Gọi đường tròn (B; BI) giao (C; CI) tại K khác I thì K cố định.
Góc I B M ^ là góc ở tâm chắn cung I M ⏜ và I K M ^ là góc nội tiếp chắn cung I M ⏜ , suy ra I K M ^ = 1 2 I B M ^ (1).
Tương tự I K N ^ = 1 2 I C N ^ (2).
Theo câu 1) B, I, Q, C thuộc một đường tròn, suy ra I B M ^ = I B Q ^ = I C Q ^ = I C N ^ (3).
Từ (1), (2) và (3), suy ra I K M ^ = I K N ^ ⇒ K M ≡ K N .
Vậy MN đi qua K cố định.
Đúng 0
Bình luận (0)
Cho tam giác ABC,một đường tròn tâm O nội tiếp tam giác ABC tiếp xúc với BC ở D.Đường tròn tâm I bàn tiếp trong góc A của tam giác ABC.Vẽ đường kính DE.Gọi M,N là tiếp điểm của đường tròn tâm O,I với AB.Chứng minh:a)OA/IAOM/INb)A,E,F thẳng hàng
Đọc tiếp
Cho tam giác ABC,một đường tròn tâm O nội tiếp tam giác ABC tiếp xúc với BC ở D.Đường tròn tâm I bàn tiếp trong góc A của tam giác ABC.Vẽ đường kính DE.Gọi M,N là tiếp điểm của đường tròn tâm O,I với AB.Chứng minh:
a)OA/IA=OM/IN
b)A,E,F thẳng hàng
Cho tam giác ABC có góc B=60, R=2, I là tâm đường tròn nội tiếp tam giác ABC. Tìm bán kính đường tròn ngoại tiếp tam giác AIC.
TOÁN 10. :)
cho tam giác ABC nội tiếp đường tròn O,đường tròn K tiếp xúc trong vs đtròn O tại T và tiếp xúc 2 cạnh AB,AC tại E,F chưng minh tâm I đtròn nội tiếp tam giác ABC là trung điểm EF
Bổ sung: ΔABC cân tại A
ΔABC cân tại A
=>AO đi qua trug diểm I của EF
Vẽ IK vuông góc AB tại K, gọi H và G lần lượt là giao của OA với BC và(O)
Vì OE vuông góc AB, IK vuông goc AB, GB vuông góc AB
=>OE//IK//GB
ΔABG có IK//GB
nên IK/BG=AI/AG
=>IK=AI*BG/AG
ΔABH có EI//BH
ΔABE có OE//BG
=>IH/AH=BE/BA=OG/AG và AE/AB=AI/AH
=>IH=AH*OE/AE
ΔABG có OE//BG
nên AB/AE=BG/OE
AH/AI=AB/AE=BG/OE
=>AH*OE=AI*BG
=>AH*OG=AI*BG
=>IK=IH
=>ĐPCM
Đúng 0
Bình luận (1)















