Tính tổng các giá trị của m trên đoạn \(\left[-\dfrac{\pi}{3};\dfrac{\pi}{2}\right]\) có nghĩa là \(x\in\left[-\dfrac{\pi}{3};\dfrac{\pi}{2}\right]\) pk?

\(\Rightarrow cosx\in\left[0;1\right]\)

\(y=2cos^2x+cosx-1+\left|2m-1\right|\)

Đặt \(t=cosx;t\in\left[0;1\right]\)

\(y=2t^2+t-1+\left|2m-1\right|\)

Xét BBT của \(f\left(t\right)=2t^2+t-1;t\in\left[0;1\right]\)

\(\Rightarrow f\left(t\right)_{min}=-1\Leftrightarrow t=0\Leftrightarrow cosx=0\)\(\Leftrightarrow x=\dfrac{\pi}{2}\)

\(\Rightarrow y\ge-1+\left|2m-1\right|\)

Để \(y_{min}=2\Leftrightarrow-1+\left|2m-1\right|=2\)\(\Leftrightarrow m=2;m=-1\)

\(\Rightarrow\)Tổng m bằng \(1\)

Chọn C.

+) TXĐ: D = R

+) Ta có đạo hàm y’ = ( x² - 2( m + 3) x + 4) .e^x .

Hàm số nghịch biến trên TXĐ khi y’ = ( x² - 2( m + 3) x + 4) .e^x ≤ 0 mọi x

Chọn A

Hàm số y = f(x) =  2 x + m x - 1 . xác định và liên tục trên [2;3].

Với m = -2, hàm số trở thành y = 2(không thỏa)

Với  ta có: 

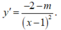
Khi đó hàm số luôn đồng biến hoặc nghịch biến trên [2;3]

Suy ra 

Do đó: 

Theo giả thiết 

Vậy tổng các giá trị của tham số  thỏa mãn yêu cầu bài toán là: -4.

Nhận xét: đề bài cho thêm dấu giá trị tuyệt đối ở trong biểu thức  là không cần thiết.

Chọn A

Hàm số y = f(x) =  2 x + m x - 1 xác định và liên tục trên [2;3]

 Với m = -2, hàm số trở thành y = 2  (không thỏa).

Với m ≠ 2, ta có: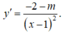 

Khi đó hàm số luôn đồng biến hoặc nghịch biến trên [2;3]

Suy ra 

Do đó: 

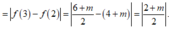
Theo giả thiết 

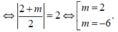
Vậy tổng các giá trị của tham số  thỏa mãn yêu cầu bài toán là: -4.

Nhận xét: đề bài cho thêm dấu giá trị tuyệt đối ở trong biểu thức   là không cần thiết.

Đáp án D

Có  y ' = − m 2 − 1 x − m 2 < 0 , ∀ x ∈ 1 ; 2   . Do đó hàm số là hàm nghịch biến trên [1;2], từ đó  max x ∈ 1 ; 2 y = y 1 = m + 1 1 − m = − 2 ⇔ m = 3.

f'(x)>0 với mọi x khác -8, suy ra hàm số đã cho đồng biến trên [0;3].

Giá trị nhỏ nhất của f(x) trên [0;3] là (-m^2)/8. Ta có: (-m^2)/8=2.

Suy ra, không có giá trị nào của số thực m thỏa yêu cầu đề bài.

Hàm tính tổng:

=Sum(a,b,c,...)

Hàm tính trung bình cộng:

=average(a,b,c,...)