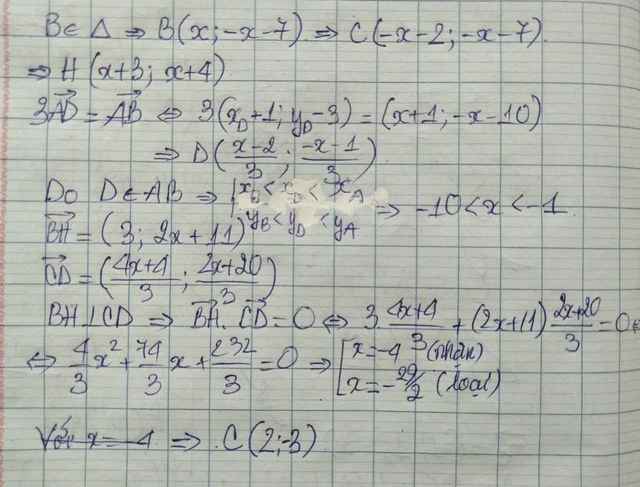trog mp tọa độ Oxy cho các điểm M(x=2m-1; y=m+3) với M thuộc R. tìm tập hợp các điểm M khi m thay đổi

Những câu hỏi liên quan
1) Trên mp tọa độ Oxy, cho đường thẳng y=(2m+1)x-4m-1 và điểm A(-2;3). Tìm m để khoảng cách từ A đến đường thẳng trên là lớn nhất.
2) Trên mp tọa độ Oxy, cho A(2;3) và điểm B(1;-4) và điểm C nằm trên trục Ox. Tìm tọa độ điểm C để tam giác ABC có chu vi nhỏ nhất.
Trong mp tọa độ Oxy cho (P): y =x^2, đg thẳng (d): y= 2mx - 2m +3 (m là tham số)
a. Tìm m để (d) đi qua điểm M (2;5)
b. CM (d) và (P) cắt nhau tại 2 điểm pbiệt với mọi m. Gọi y1, y2 là các tung độ giao điểm của (d) và (P). Tìm m sao cho: y1 + y2 < 9
a) Để (d) đi qua M(2;5) thì Thay x=2 và y=5 vào (d), ta được:
\(2m\cdot2-2m+3=5\)
\(\Leftrightarrow4m-2m=5-3\)
\(\Leftrightarrow2m=2\)
\(\Leftrightarrow m=1\)
Vậy: Để (d) đi qua M(2;5) thì m=1
b) Phương trình hoành độ của (d) và (P) là:
\(x^2=2mx-2m+3\)
\(\Leftrightarrow x^2-2mx+2m-3=0\)
\(\Delta=\left(-2m\right)^2-4\cdot1\cdot\left(2m-3\right)=4m^2-4\left(2m-3\right)\)
\(\Leftrightarrow\Delta=4m^2-8m+12=\left(2m\right)^2-2\cdot2m\cdot2+4+8\)
\(\Leftrightarrow\Delta=\left(2m-2\right)^2+8>0\forall m\)
Suy ra: (d) và (P) luôn cắt nhau tại hai điểm phân biệt với mọi m
Đúng 3
Bình luận (0)
Trong mp tọa độ Oxy cho tam giác ABC. Biết phương trình các đường thẳng chứa đường cao BH, phân giác AD lần lượt làx+4y+5=0; x-y+2=0; điểm M(1; 2) thuộc đường thẳng AB. Tính tọa độ AB
1) cho pt x2 - 3x + m 0 (1)
a) giải pt khi m1
b) tìm các gtri của m thỏa điều kiện có 2 nghiệm phân biệt và sqrt{x_1^{2^{ }}+1}+sqrt{x_{2_{ }}^2+1}3
2) Trog mp tọa độ Oxy Cho (P) : y x2 và (d) : y 2mx -2m +3
a) tìm tọa độ các điểm thuộc (P) biết tung độ 2
b) CMR ; (P) và (d) cắt nhau tại 2 điểm phân biệt với mọi m
c) gọi y1 , y2 là tung độ giao điểm của (P) và (d) . Tìm m để y1 + y2 9
Đọc tiếp
1) cho pt x2 - 3x + m = 0 (1)
a) giải pt khi m=1
b) tìm các gtri của m thỏa điều kiện có 2 nghiệm phân biệt và \(\sqrt{x_1^{2^{ }}+1}+\sqrt{x_{2_{ }}^2+1}=3\)
2) Trog mp tọa độ Oxy Cho (P) : y = x2 và (d) : y = 2mx -2m +3
a) tìm tọa độ các điểm thuộc (P) biết tung độ =2
b) CMR ; (P) và (d) cắt nhau tại 2 điểm phân biệt với mọi m
c) gọi y1 , y2 là tung độ giao điểm của (P) và (d) . Tìm m để y1 + y2 < 9
Trong mp với hệ tọa đô Oxy cho hai điểm A(1;-2), B(-4;5). Tìm tọa độ điểm M trên trục Oy sao cho 3 điểm M,A,B thẳng hàng
Gọi \(M\left(0;m\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(-1;m+2\right)\\\overrightarrow{AB}=\left(-5;7\right)\end{matrix}\right.\)
3 điểm M;A;B thẳng hàng khi:
\(\dfrac{-1}{-5}=\dfrac{m+2}{7}\Rightarrow m=-\dfrac{3}{5}\)
\(\Rightarrow M\left(0;-\dfrac{3}{5}\right)\)
Đúng 2
Bình luận (0)
Trên mặt phẳng Oxy cho đường tẳng (d) y=(2m+1)x-m^2-m+6 parabol (P) y=x^2
a) Tìm tọa độ giao điểm khi m=0
b) Tìm các số dương m để (d) cắt (P) tại hai điểm phân biệt có hoành độ x1,x2 sao cho x1-x2=25
Trong MP tọa độ Oxy cho tam giác ABC cân tại A(-1;3). D thuộc AB sao cho AB=3AD. Kẻ BH vuông với CD. M(1/2;-3/2) là trung điểm HC. B thuộc đường thẳng đenta có tọa độ x+y+7=0
Tìm tọa độ điểm C
Trong mặt phẳng tọa độ Oxy, Cho tam giác ABC biết A(–2 ; 2), B(2 ; – 1), C(5 ; 3 ) và điểm E(–1; 0 ). a) Chứng minh rằng tam giác ABC cân.Tính diện tích tam giác ABC. b) Tìm tọa độ các điểm M(m; 2m-5) sao cho MO=√5AE5AE ( biết O là gốc tọa độ và m lớn hơn 0 ).
a: \(AB=\sqrt{\left[2-\left(-2\right)\right]^2+\left(-1-2\right)^2}=5\)
\(BC=\sqrt{\left(5-2\right)^2+\left(3+1\right)^2}=5\)
Do đó: AB=BC
hay ΔABC cân tại B
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, Cho tam giác ABC biết A(–2 ; 2), B(2 ; – 1), C(5 ; 3 ) và điểm E(–1; 0 ). a) Chứng minh rằng tam giác ABC cân.Tính diện tích tam giác ABC. b) Tìm tọa độ các điểm M(m; 2m-5) sao cho MO=\(\sqrt{5}AE\) ( biết O là gốc tọa độ và m lớn hơn 0 ).
a: \(AB=\sqrt{\left(2+2\right)^2+\left(-1-2\right)^2}=5\)
\(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
Do đó: ΔABC cân tại B
Đúng 0
Bình luận (1)